Kernel Stochastic Configuration Networks for Nonlinear Regression

Stochastic configuration networks (SCNs), as a class of randomized learner models, are featured by its way of random parameters assignment in the light of a supervisory mechanism, resulting in the universal approximation property at algorithmic level. This paper presents a kernel version of SCNs, termed KSCNs, aiming to enhance model's representation learning capability and performance stability. The random bases of a built SCN model can be used to span a reproducing kernel Hilbert space (RKHS), followed by our proposed algorithm for constructing KSCNs. It is shown that the data distribution in the reconstructive space is favorable for regression solving and the proposed KSCN learner models hold the universal approximation property. Three benchmark datasets including two industrial datasets are used in this study for performance evaluation. Experimental results with comparisons against existing solutions clearly demonstrate that the proposed KSCN remarkably outperforms the original SCNs and some typical kernel methods for resolving nonlinear regression problems in terms of the learning performance, the model's stability and robustness with respect to the kernel parameter settings.

Deeper Insights into Learning Performance of Stochastic Configuration Networks

Stochastic Configuration Networks (SCNs) are a class of randomized neural networks that integrate randomized algorithms within an incremental learning framework. A defining feature of SCNs is the supervisory mechanism, which adaptively adjusts the distribution to generate effective random basis functions, thereby enabling error-free learning. In this paper, we present a comprehensive analysis of the impact of the supervisory mechanism on the learning performance of SCNs. Our findings reveal that the current SCN framework evaluates the effectiveness of each random basis function in reducing residual errors using a lower bound on its error reduction potential, which constrains SCNs' overall learning efficiency. Specifically, SCNs may fail to consistently select the most effective random candidate as the new basis function during each training iteration. To overcome this problem, we propose a novel method for evaluating the hidden layer's output matrix, supported by a new supervisory mechanism that accurately assesses the error reduction potential of random basis functions without requiring the computation of the Moore-Penrose inverse of the output matrix. This approach enhances the selection of basis functions, reducing computational complexity and improving the overall scalability and learning capabilities of SCNs. We introduce a Recursive Moore-Penrose Inverse-SCN (RMPI-SCN) training scheme based on the new supervisory mechanism and demonstrate its effectiveness through simulations over some benchmark datasets. Experiments show that RMPI-SCN outperforms the conventional SCN in terms of learning capability, underscoring its potential to advance the SCN framework for large-scale data modeling applications.

Deep Recurrent Stochastic Configuration Networks for Modelling Nonlinear Dynamic Systems

Deep learning techniques have shown promise in many domain applications. This paper proposes a novel deep reservoir computing framework, termed deep recurrent stochastic configuration network (DeepRSCN) for modelling nonlinear dynamic systems. DeepRSCNs are incrementally constructed, with all reservoir nodes directly linked to the final output. The random parameters are assigned in the light of a supervisory mechanism, ensuring the universal approximation property of the built model. The output weights are updated online using the projection algorithm to handle the unknown dynamics. Given a set of training samples, DeepRSCNs can quickly generate learning representations, which consist of random basis functions with cascaded input and readout weights. Experimental results over a time series prediction, a nonlinear system identification problem, and two industrial data predictive analyses demonstrate that the proposed DeepRSCN outperforms the single-layer network in terms of modelling efficiency, learning capability, and generalization performance.

Self-Organizing Recurrent Stochastic Configuration Networks for Nonstationary Data Modelling

Recurrent stochastic configuration networks (RSCNs) are a class of randomized learner models that have shown promise in modelling nonlinear dynamics. In many fields, however, the data generated by industry systems often exhibits nonstationary characteristics, leading to the built model performing well on the training data but struggling with the newly arriving data. This paper aims at developing a self-organizing version of RSCNs, termed as SORSCNs, to enhance the continuous learning ability of the network for modelling nonstationary data. SORSCNs can autonomously adjust the network parameters and reservoir structure according to the data streams acquired in real-time. The output weights are updated online using the projection algorithm, while the network structure is dynamically adjusted in the light of the recurrent stochastic configuration algorithm and an improved sensitivity analysis. Comprehensive comparisons among the echo state network (ESN), online self-learning stochastic configuration network (OSL-SCN), self-organizing modular ESN (SOMESN), RSCN, and SORSCN are carried out. Experimental results clearly demonstrate that the proposed SORSCNs outperform other models with sound generalization, indicating great potential in modelling nonlinear systems with nonstationary dynamics.

Recurrent Stochastic Configuration Networks for Temporal Data Analytics

Temporal data modelling techniques with neural networks are useful in many domain applications, including time-series forecasting and control engineering. This paper aims at developing a recurrent version of stochastic configuration networks (RSCNs) for problem solving, where we have no underlying assumption on the dynamic orders of the input variables. Given a collection of historical data, we first build an initial RSCN model in the light of a supervisory mechanism, followed by an online update of the output weights by using a projection algorithm. Some theoretical results are established, including the echo state property, the universal approximation property of RSCNs for both the offline and online learnings, and the convergence of the output weights. The proposed RSCN model is remarkably distinguished from the well-known echo state networks (ESNs) in terms of the way of assigning the input random weight matrix and a special structure of the random feedback matrix. A comprehensive comparison study among the long short-term memory (LSTM) network, the original ESN, and several state-of-the-art ESN methods such as the simple cycle reservoir (SCR), the polynomial ESN (PESN), the leaky-integrator ESN (LIESN) and RSCN is carried out. Numerical results clearly indicate that the proposed RSCN performs favourably over all of the datasets.

Stochastic Configuration Machines: FPGA Implementation

Neural networks for industrial applications generally have additional constraints such as response speed, memory size and power usage. Randomized learners can address some of these issues. However, hardware solutions can provide better resource reduction whilst maintaining the model's performance. Stochastic configuration networks (SCNs) are a prime choice in industrial applications due to their merits and feasibility for data modelling. Stochastic Configuration Machines (SCMs) extend this to focus on reducing the memory constraints by limiting the randomized weights to a binary value with a scalar for each node and using a mechanism model to improve the learning performance and result interpretability. This paper aims to implement SCM models on a field programmable gate array (FPGA) and introduce binary-coded inputs to the algorithm. Results are reported for two benchmark and two industrial datasets, including SCM with single-layer and deep architectures.

Stochastic Configuration Machines for Industrial Artificial Intelligence

Real-time predictive modelling with desired accuracy is highly expected in industrial artificial intelligence (IAI), where neural networks play a key role. Neural networks in IAI require powerful, high-performance computing devices to operate a large number of floating point data. Based on stochastic configuration networks (SCNs), this paper proposes a new randomized learner model, termed stochastic configuration machines (SCMs), to stress effective modelling and data size saving that are useful and valuable for industrial applications. Compared to SCNs and random vector functional-link (RVFL) nets with binarized implementation, the model storage of SCMs can be significantly compressed while retaining favourable prediction performance. Besides the architecture of the SCM learner model and its learning algorithm, as an important part of this contribution, we also provide a theoretical basis on the learning capacity of SCMs by analysing the model's complexity. Experimental studies are carried out over some benchmark datasets and three industrial applications. The results demonstrate that SCM has great potential for dealing with industrial data analytics.

Two Dimensional Stochastic Configuration Networks for Image Data Analytics

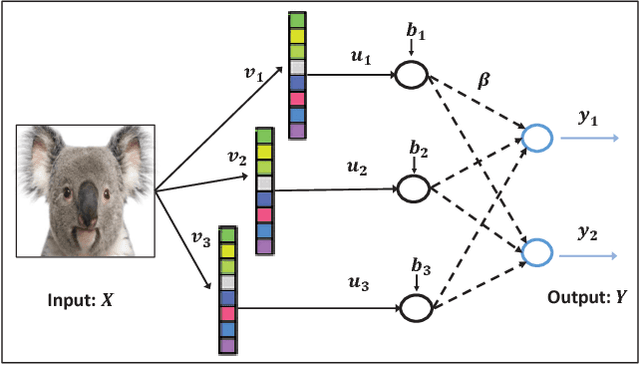
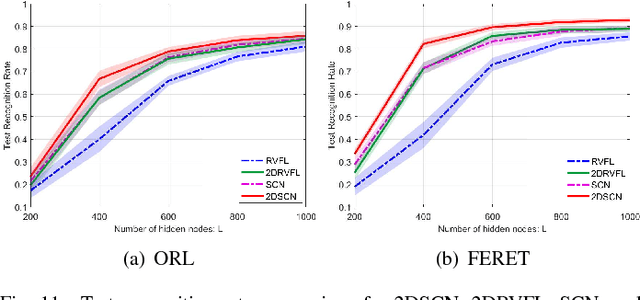
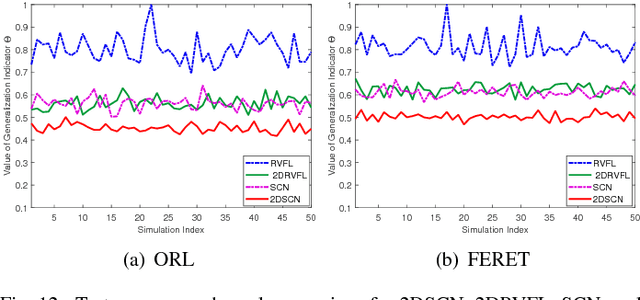
Stochastic configuration networks (SCNs) as a class of randomized learner model have been successfully employed in data analytics due to its universal approximation capability and fast modelling property. The technical essence lies in stochastically configuring hidden nodes (or basis functions) based on a supervisory mechanism rather than data-independent randomization as usually adopted for building randomized neural networks. Given image data modelling tasks, the use of one-dimensional SCNs potentially demolishes the spatial information of images, and may result in undesirable performance. This paper extends the original SCNs to two-dimensional version, termed 2DSCNs, for fast building randomized learners with matrix-inputs. Some theoretical analyses on the goodness of 2DSCNs against SCNs, including the complexity of the random parameter space, and the superiority of generalization, are presented. Empirical results over one regression, four benchmark handwritten digits classification, and two human face recognition datasets demonstrate that the proposed 2DSCNs perform favourably and show good potential for image data analytics.

Deep Stacked Stochastic Configuration Networks for Non-Stationary Data Streams

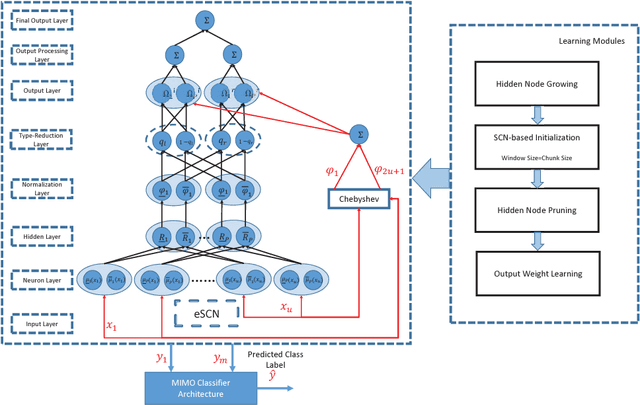
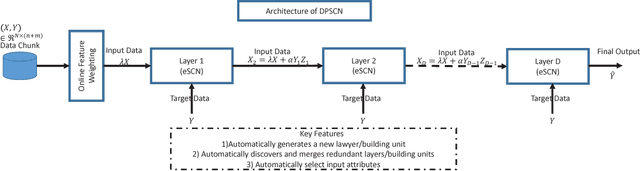
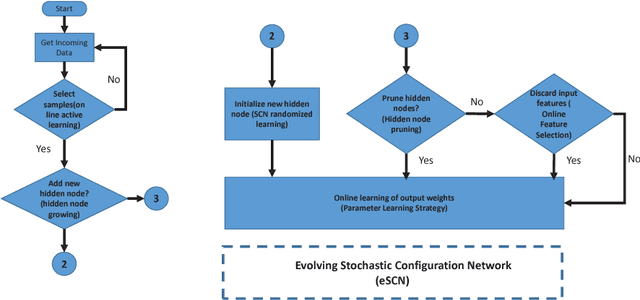
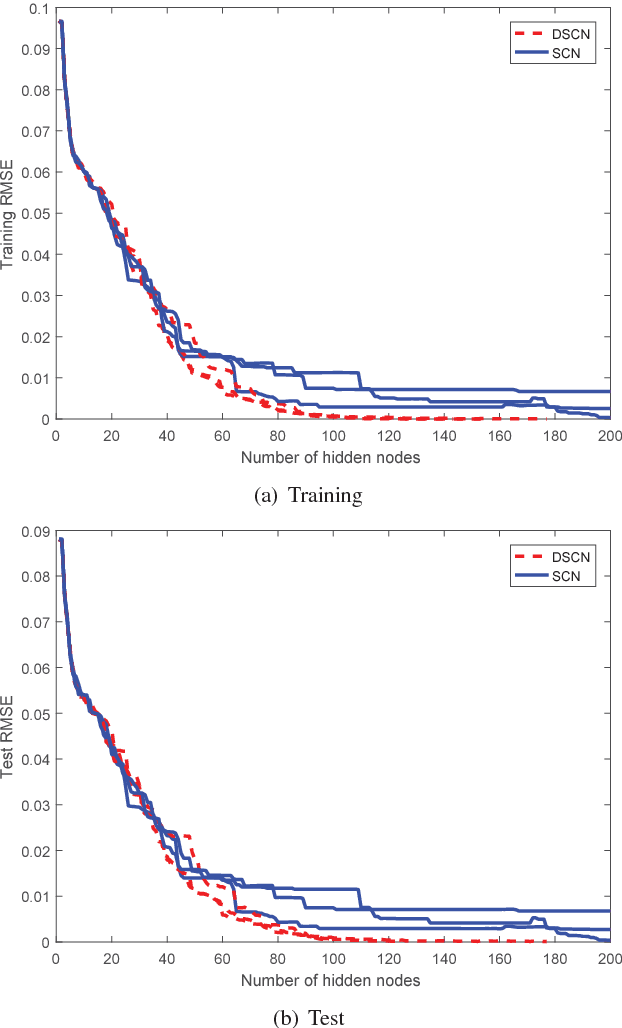
The concept of stochastic configuration networks (SCNs) others a solid framework for fast implementation of feedforward neural networks through randomized learning. Unlike conventional randomized approaches, SCNs provide an avenue to select appropriate scope of random parameters to ensure the universal approximation property. In this paper, a deep version of stochastic configuration networks, namely deep stacked stochastic configuration network (DSSCN), is proposed for modeling non-stationary data streams. As an extension of evolving stochastic connfiguration networks (eSCNs), this work contributes a way to grow and shrink the structure of deep stochastic configuration networks autonomously from data streams. The performance of DSSCN is evaluated by six benchmark datasets. Simulation results, compared with prominent data stream algorithms, show that the proposed method is capable of achieving comparable accuracy and evolving compact and parsimonious deep stacked network architecture.

Deep Stochastic Configuration Networks with Universal Approximation Property

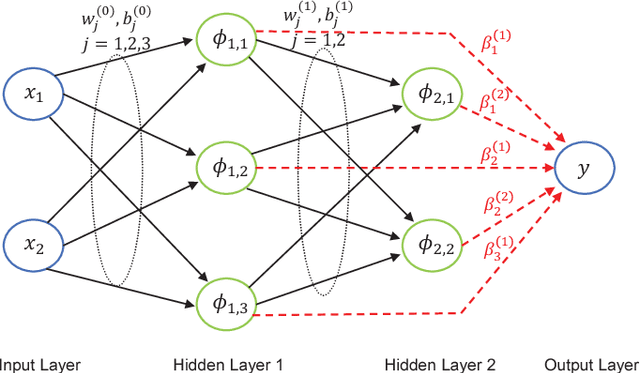
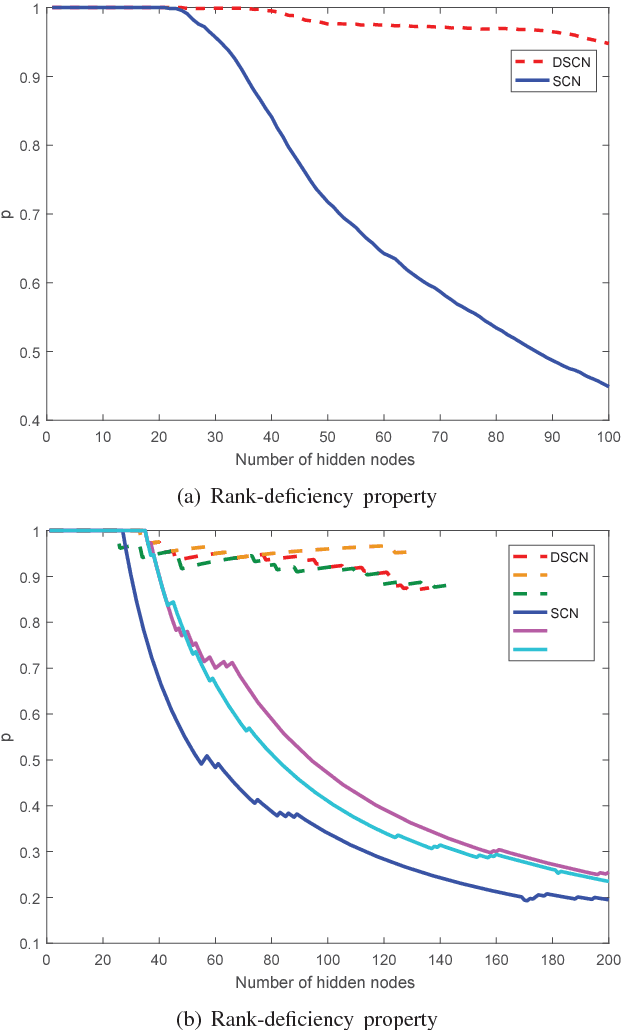
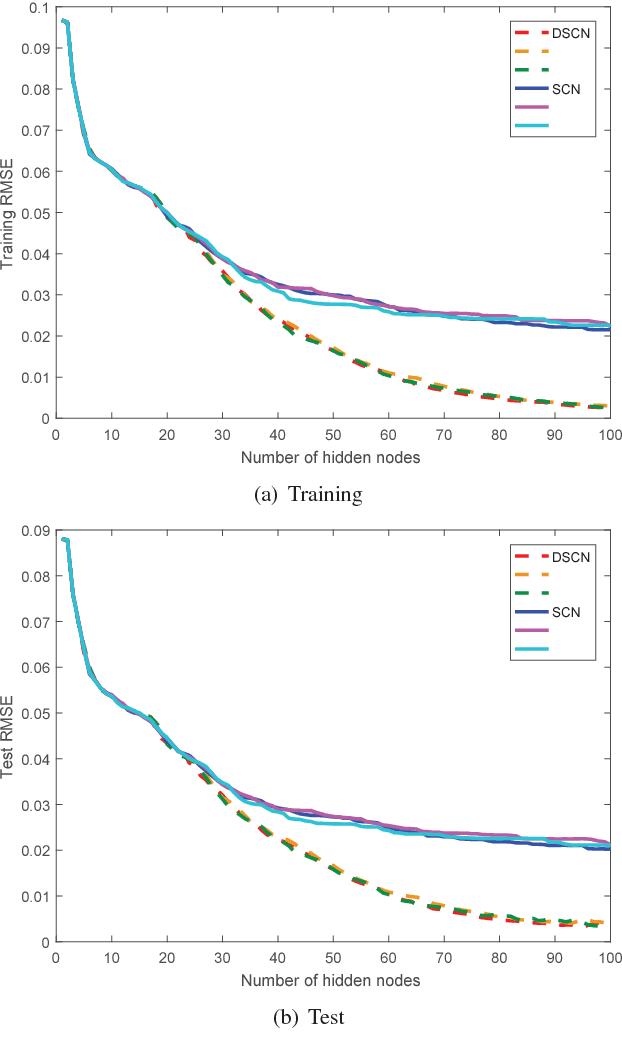
This paper develops a randomized approach for incrementally building deep neural networks, where a supervisory mechanism is proposed to constrain the random assignment of the weights and biases, and all the hidden layers have direct links to the output layer. A fundamental result on the universal approximation property is established for such a class of randomized leaner models, namely deep stochastic configuration networks (DeepSCNs). A learning algorithm is presented to implement DeepSCNs with either specific architecture or self-organization. The read-out weights attached with all direct links from each hidden layer to the output layer are evaluated by the least squares method. Given a set of training examples, DeepSCNs can speedily produce a learning representation, that is, a collection of random basis functions with the cascaded inputs together with the read-out weights. An empirical study on a function approximation is carried out to demonstrate some properties of the proposed deep learner model.