GenPhys: From Physical Processes to Generative Models

Since diffusion models (DM) and the more recent Poisson flow generative models (PFGM) are inspired by physical processes, it is reasonable to ask: Can physical processes offer additional new generative models? We show that the answer is yes. We introduce a general family, Generative Models from Physical Processes (GenPhys), where we translate partial differential equations (PDEs) describing physical processes to generative models. We show that generative models can be constructed from s-generative PDEs (s for smooth). GenPhys subsume the two existing generative models (DM and PFGM) and even give rise to new families of generative models, e.g., "Yukawa Generative Models" inspired from weak interactions. On the other hand, some physical processes by default do not belong to the GenPhys family, e.g., the wave equation and the Schr\"{o}dinger equation, but could be made into the GenPhys family with some modifications. Our goal with GenPhys is to explore and expand the design space of generative models.

Autoregressive Neural TensorNet: Bridging Neural Networks and Tensor Networks for Quantum Many-Body Simulation

Quantum many-body physics simulation has important impacts on understanding fundamental science and has applications to quantum materials design and quantum technology. However, due to the exponentially growing size of the Hilbert space with respect to the particle number, a direct simulation is intractable. While representing quantum states with tensor networks and neural networks are the two state-of-the-art methods for approximate simulations, each has its own limitations in terms of expressivity and optimization. To address these challenges, we develop a novel architecture, Autoregressive Neural TensorNet (ANTN), which bridges tensor networks and autoregressive neural networks. We show that Autoregressive Neural TensorNet parameterizes normalized wavefunctions with exact sampling, generalizes the expressivity of tensor networks and autoregressive neural networks, and inherits a variety of symmetries from autoregressive neural networks. We demonstrate our approach on the 2D $J_1$-$J_2$ Heisenberg model with different systems sizes and coupling parameters, outperforming both tensor networks and autoregressive neural networks. Our work opens up new opportunities for both scientific simulations and machine learning applications.

Artificial intelligence for artificial materials: moiré atom

Moir\'e engineering in atomically thin van der Waals heterostructures creates artificial quantum materials with designer properties. We solve the many-body problem of interacting electrons confined to a moir\'e superlattice potential minimum (the moir\'e atom) using a 2D fermionic neural network. We show that strong Coulomb interactions in combination with the anisotropic moir\'e potential lead to striking ``Wigner molecule" charge density distributions observable with scanning tunneling microscopy.

Q-Flow: Generative Modeling for Differential Equations of Open Quantum Dynamics with Normalizing Flows

Studying the dynamics of open quantum systems holds the potential to enable breakthroughs both in fundamental physics and applications to quantum engineering and quantum computation. Due to the high-dimensional nature of the problem, customized deep generative neural networks have been instrumental in modeling the high-dimensional density matrix $\rho$, which is the key description for the dynamics of such systems. However, the complex-valued nature and normalization constraints of $\rho$, as well as its complicated dynamics, prohibit a seamless connection between open quantum systems and the recent advances in deep generative modeling. Here we lift that limitation by utilizing a reformulation of open quantum system dynamics to a partial differential equation (PDE) for a corresponding probability distribution $Q$, the Husimi Q function. Thus, we model the Q function seamlessly with off-the-shelf deep generative models such as normalizing flows. Additionally, we develop novel methods for learning normalizing flow evolution governed by high-dimensional PDEs, based on the Euler method and the application of the time-dependent variational principle. We name the resulting approach Q-Flow and demonstrate the scalability and efficiency of Q-Flow on open quantum system simulations, including the dissipative harmonic oscillator and the dissipative bosonic model. Q-Flow is superior to conventional PDE solvers and state-of-the-art physics-informed neural network solvers, especially in high-dimensional systems.

Geometry of contact: contact planning for multi-legged robots via spin models duality

Contact planning is crucial in locomoting systems.Specifically, appropriate contact planning can enable versatile behaviors (e.g., sidewinding in limbless locomotors) and facilitate speed-dependent gait transitions (e.g., walk-trot-gallop in quadrupedal locomotors). The challenges of contact planning include determining not only the sequence by which contact is made and broken between the locomotor and the environments, but also the sequence of internal shape changes (e.g., body bending and limb shoulder joint oscillation). Most state-of-art contact planning algorithms focused on conventional robots (e.g.biped and quadruped) and conventional tasks (e.g. forward locomotion), and there is a lack of study on general contact planning in multi-legged robots. In this paper, we show that using geometric mechanics framework, we can obtain the global optimal contact sequence given the internal shape changes sequence. Therefore, we simplify the contact planning problem to a graph optimization problem to identify the internal shape changes. Taking advantages of the spatio-temporal symmetry in locomotion, we map the graph optimization problem to special cases of spin models, which allows us to obtain the global optima in polynomial time. We apply our approach to develop new forward and sidewinding behaviors in a hexapod and a 12-legged centipede. We verify our predictions using numerical and robophysical models, and obtain novel and effective locomotion behaviors.

Simulating 2+1D Lattice Quantum Electrodynamics at Finite Density with Neural Flow Wavefunctions

We present a neural flow wavefunction, Gauge-Fermion FlowNet, and use it to simulate 2+1D lattice compact quantum electrodynamics with finite density dynamical fermions. The gauge field is represented by a neural network which parameterizes a discretized flow-based transformation of the amplitude while the fermionic sign structure is represented by a neural net backflow. This approach directly represents the $U(1)$ degree of freedom without any truncation, obeys Guass's law by construction, samples autoregressively avoiding any equilibration time, and variationally simulates Gauge-Fermion systems with sign problems accurately. In this model, we investigate confinement and string breaking phenomena in different fermion density and hopping regimes. We study the phase transition from the charge crystal phase to the vacuum phase at zero density, and observe the phase seperation and the net charge penetration blocking effect under magnetic interaction at finite density. In addition, we investigate a magnetic phase transition due to the competition effect between the kinetic energy of fermions and the magnetic energy of the gauge field. With our method, we further note potential differences on the order of the phase transitions between a continuous $U(1)$ system and one with finite truncation. Our state-of-the-art neural network approach opens up new possibilities to study different gauge theories coupled to dynamical matter in higher dimensions.

Gauge Equivariant Neural Networks for 2+1D U Gauge Theory Simulations in Hamiltonian Formulation

Gauge Theory plays a crucial role in many areas in science, including high energy physics, condensed matter physics and quantum information science. In quantum simulations of lattice gauge theory, an important step is to construct a wave function that obeys gauge symmetry. In this paper, we have developed gauge equivariant neural network wave function techniques for simulating continuous-variable quantum lattice gauge theories in the Hamiltonian formulation. We have applied the gauge equivariant neural network approach to find the ground state of 2+1-dimensional lattice gauge theory with U(1) gauge group using variational Monte Carlo. We have benchmarked our approach against the state-of-the-art complex Gaussian wave functions, demonstrating improved performance in the strong coupling regime and comparable results in the weak coupling regime.

Koopman Operator learning for Accelerating Quantum Optimization and Machine Learning

Finding efficient optimization methods plays an important role for quantum optimization and quantum machine learning on near-term quantum computers. While backpropagation on classical computers is computationally efficient, obtaining gradients on quantum computers is not, because the computational complexity usually scales with the number of parameters and measurements. In this paper, we connect Koopman operator theory, which has been successful in predicting nonlinear dynamics, with natural gradient methods in quantum optimization. We propose a data-driven approach using Koopman operator learning to accelerate quantum optimization and quantum machine learning. We develop two new families of methods: the sliding window dynamic mode decomposition (DMD) and the neural DMD for efficiently updating parameters on quantum computers. We show that our methods can predict gradient dynamics on quantum computers and accelerate the variational quantum eigensolver used in quantum optimization, as well as quantum machine learning. We further implement our Koopman operator learning algorithm on a real IBM quantum computer and demonstrate their practical effectiveness.

Infinite Neural Network Quantum States

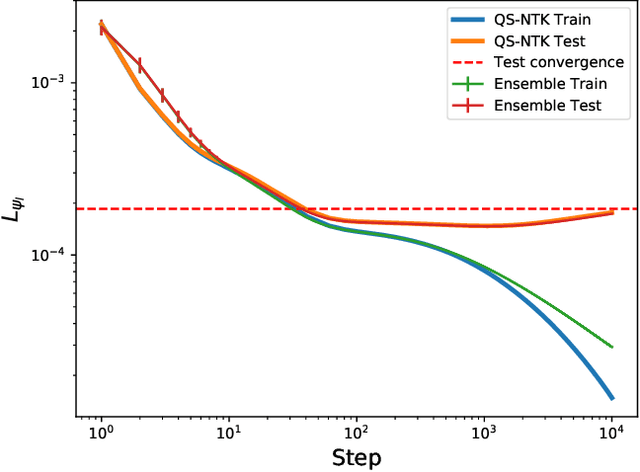
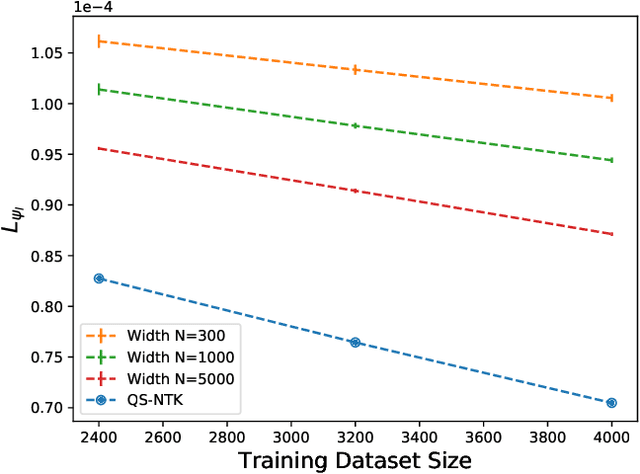
We study infinite limits of neural network quantum states ($\infty$-NNQS), which exhibit representation power through ensemble statistics, and also tractable gradient descent dynamics. Ensemble averages of Renyi entropies are expressed in terms of neural network correlators, and architectures that exhibit volume-law entanglement are presented. A general framework is developed for studying the gradient descent dynamics of neural network quantum states (NNQS), using a quantum state neural tangent kernel (QS-NTK). For $\infty$-NNQS the training dynamics is simplified, since the QS-NTK becomes deterministic and constant. An analytic solution is derived for quantum state supervised learning, which allows an $\infty$-NNQS to recover any target wavefunction. Numerical experiments on finite and infinite NNQS in the transverse field Ising model and Fermi Hubbard model demonstrate excellent agreement with theory. $\infty$-NNQS opens up new opportunities for studying entanglement and training dynamics in other physics applications, such as in finding ground states.

Spacetime Neural Network for High Dimensional Quantum Dynamics

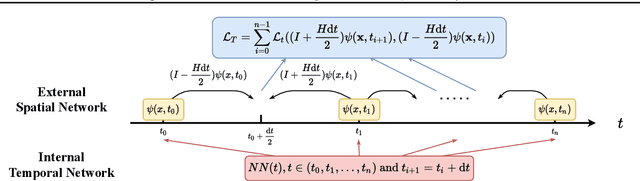
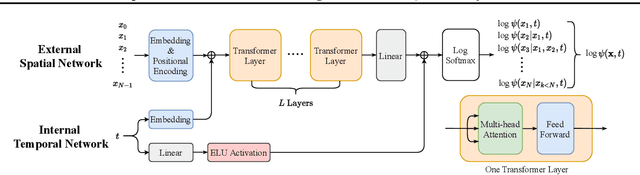
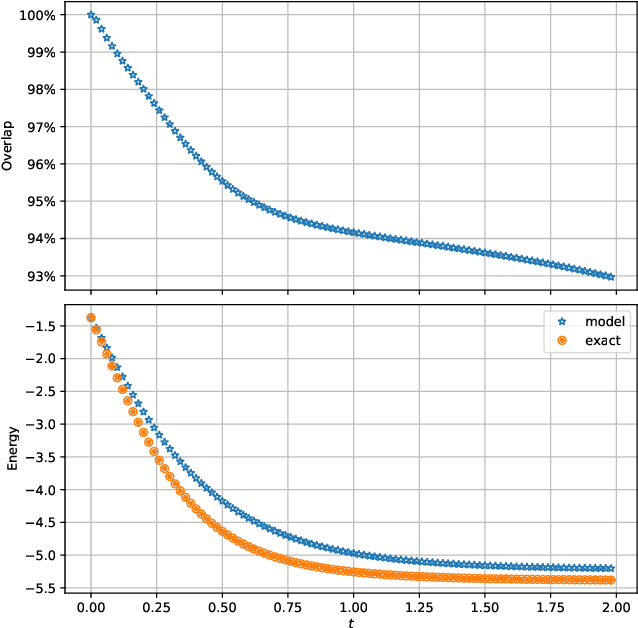
We develop a spacetime neural network method with second order optimization for solving quantum dynamics from the high dimensional Schr\"{o}dinger equation. In contrast to the standard iterative first order optimization and the time-dependent variational principle, our approach utilizes the implicit mid-point method and generates the solution for all spatial and temporal values simultaneously after optimization. We demonstrate the method in the Schr\"{o}dinger equation with a self-normalized autoregressive spacetime neural network construction. Future explorations for solving different high dimensional differential equations are discussed.