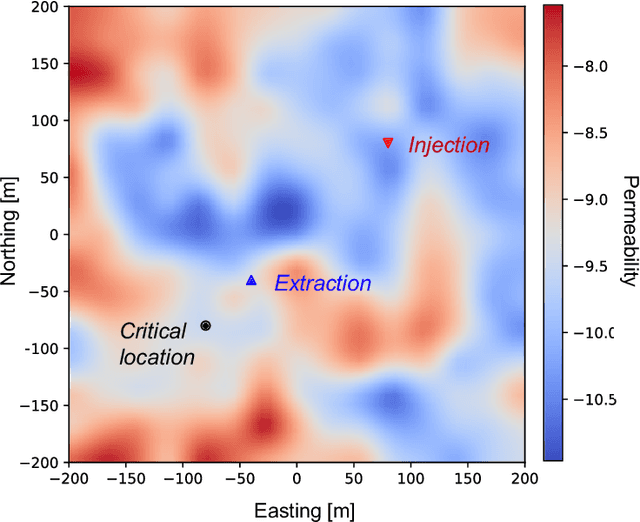
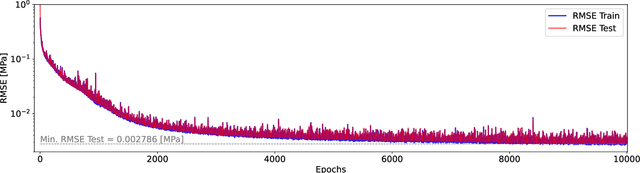
Differentiable multiphase flow model for physics-informed machine learning in reservoir pressure management

Accurate subsurface reservoir pressure control is extremely challenging due to geological heterogeneity and multiphase fluid-flow dynamics. Predicting behavior in this setting relies on high-fidelity physics-based simulations that are computationally expensive. Yet, the uncertain, heterogeneous properties that control these flows make it necessary to perform many of these expensive simulations, which is often prohibitive. To address these challenges, we introduce a physics-informed machine learning workflow that couples a fully differentiable multiphase flow simulator, which is implemented in the DPFEHM framework with a convolutional neural network (CNN). The CNN learns to predict fluid extraction rates from heterogeneous permeability fields to enforce pressure limits at critical reservoir locations. By incorporating transient multiphase flow physics into the training process, our method enables more practical and accurate predictions for realistic injection-extraction scenarios compare to previous works. To speed up training, we pretrain the model on single-phase, steady-state simulations and then fine-tune it on full multiphase scenarios, which dramatically reduces the computational cost. We demonstrate that high-accuracy training can be achieved with fewer than three thousand full-physics multiphase flow simulations -- compared to previous estimates requiring up to ten million. This drastic reduction in the number of simulations is achieved by leveraging transfer learning from much less expensive single-phase simulations.

LLM-Assisted Translation of Legacy FORTRAN Codes to C++: A Cross-Platform Study

Large Language Models (LLMs) are increasingly being leveraged for generating and translating scientific computer codes by both domain-experts and non-domain experts. Fortran has served as one of the go to programming languages in legacy high-performance computing (HPC) for scientific discoveries. Despite growing adoption, LLM-based code translation of legacy code-bases has not been thoroughly assessed or quantified for its usability. Here, we studied the applicability of LLM-based translation of Fortran to C++ as a step towards building an agentic-workflow using open-weight LLMs on two different computational platforms. We statistically quantified the compilation accuracy of the translated C++ codes, measured the similarity of the LLM translated code to the human translated C++ code, and statistically quantified the output similarity of the Fortran to C++ translation.

Model-Agnostic Knowledge Guided Correction for Improved Neural Surrogate Rollout

Modeling the evolution of physical systems is critical to many applications in science and engineering. As the evolution of these systems is governed by partial differential equations (PDEs), there are a number of computational simulations which resolve these systems with high accuracy. However, as these simulations incur high computational costs, they are infeasible to be employed for large-scale analysis. A popular alternative to simulators are neural network surrogates which are trained in a data-driven manner and are much more computationally efficient. However, these surrogate models suffer from high rollout error when used autoregressively, especially when confronted with training data paucity. Existing work proposes to improve surrogate rollout error by either including physical loss terms directly in the optimization of the model or incorporating computational simulators as `differentiable layers' in the neural network. Both of these approaches have their challenges, with physical loss functions suffering from slow convergence for stiff PDEs and simulator layers requiring gradients which are not always available, especially in legacy simulators. We propose the Hybrid PDE Predictor with Reinforcement Learning (HyPER) model: a model-agnostic, RL based, cost-aware model which combines a neural surrogate, RL decision model, and a physics simulator (with or without gradients) to reduce surrogate rollout error significantly. In addition to reducing in-distribution rollout error by **47%-78%**, HyPER learns an intelligent policy that is adaptable to changing physical conditions and resistant to noise corruption. Code available at https://github.com/scailab/HyPER.

Patchfinder: Leveraging Visual Language Models for Accurate Information Retrieval using Model Uncertainty

For decades, corporations and governments have relied on scanned documents to record vast amounts of information. However, extracting this information is a slow and tedious process due to the overwhelming amount of documents. The rise of vision language models presents a way to efficiently and accurately extract the information out of these documents. The current automated workflow often requires a two-step approach involving the extraction of information using optical character recognition software, and subsequent usage of large language models for processing this information. Unfortunately, these methods encounter significant challenges when dealing with noisy scanned documents. The high information density of such documents often necessitates using computationally expensive language models to effectively reduce noise. In this study, we propose PatchFinder, an algorithm that builds upon Vision Language Models (VLMs) to address the information extraction task. First, we devise a confidence-based score, called Patch Confidence, based on the Maximum Softmax Probability of the VLMs' output to measure the model's confidence in its predictions. Then, PatchFinder utilizes that score to determine a suitable patch size, partition the input document into overlapping patches of that size, and generate confidence-based predictions for the target information. Our experimental results show that PatchFinder can leverage Phi-3v, a 4.2 billion parameter vision language model, to achieve an accuracy of 94% on our dataset of 190 noisy scanned documents, surpassing the performance of ChatGPT-4o by 18.5 percentage points.

Enhancing Code Translation in Language Models with Few-Shot Learning via Retrieval-Augmented Generation

The advent of large language models (LLMs) has significantly advanced the field of code translation, enabling automated translation between programming languages. However, these models often struggle with complex translation tasks due to inadequate contextual understanding. This paper introduces a novel approach that enhances code translation through Few-Shot Learning, augmented with retrieval-based techniques. By leveraging a repository of existing code translations, we dynamically retrieve the most relevant examples to guide the model in translating new code segments. Our method, based on Retrieval-Augmented Generation (RAG), substantially improves translation quality by providing contextual examples from which the model can learn in real-time. We selected RAG over traditional fine-tuning methods due to its ability to utilize existing codebases or a locally stored corpus of code, which allows for dynamic adaptation to diverse translation tasks without extensive retraining. Extensive experiments on diverse datasets with open LLM models such as Starcoder, Llama3-70B Instruct, CodeLlama-34B Instruct, Granite-34B Code Instruct, and Mixtral-8x22B, as well as commercial LLM models like GPT-3.5 Turbo and GPT-4o, demonstrate our approach's superiority over traditional zero-shot methods, especially in translating between Fortran and CPP. We also explored varying numbers of shots i.e. examples provided during inference, specifically 1, 2, and 3 shots and different embedding models for RAG, including Nomic-Embed, Starencoder, and CodeBERT, to assess the robustness and effectiveness of our approach.

Information Extraction from Historical Well Records Using A Large Language Model

To reduce environmental risks and impacts from orphaned wells (abandoned oil and gas wells), it is essential to first locate and then plug these wells. Although some historical documents are available, they are often unstructured, not cleaned, and outdated. Additionally, they vary widely by state and type. Manual reading and digitizing this information from historical documents are not feasible, given the high number of wells. Here, we propose a new computational approach for rapidly and cost-effectively locating these wells. Specifically, we leverage the advanced capabilities of large language models (LLMs) to extract vital information including well location and depth from historical records of orphaned wells. In this paper, we present an information extraction workflow based on open-source Llama 2 models and test them on a dataset of 160 well documents. Our results show that the developed workflow achieves excellent accuracy in extracting location and depth from clean, PDF-based reports, with a 100% accuracy rate. However, it struggles with unstructured image-based well records, where accuracy drops to 70%. The workflow provides significant benefits over manual human digitization, including reduced labor and increased automation. In general, more detailed prompting leads to improved information extraction, and those LLMs with more parameters typically perform better. We provided a detailed discussion of the current challenges and the corresponding opportunities/approaches to address them. Additionally, a vast amount of geoscientific information is locked up in old documents, and this work demonstrates that recent breakthroughs in LLMs enable us to unlock this information more broadly.

Learning the Factors Controlling Mineralization for Geologic Carbon Sequestration

We perform a set of flow and reactive transport simulations within three-dimensional fracture networks to learn the factors controlling mineral reactions. CO$_2$ mineralization requires CO$_2$-laden water, dissolution of a mineral that then leads to precipitation of a CO$_2$-bearing mineral. Our discrete fracture networks (DFN) are partially filled with quartz that gradually dissolves until it reaches a quasi-steady state. At the end of the simulation, we measure the quartz remaining in each fracture within the domain. We observe that a small backbone of fracture exists, where the quartz is fully dissolved which leads to increased flow and transport. However, depending on the DFN topology and the rate of dissolution, we observe a large variability of these changes, which indicates an interplay between the fracture network structure and the impact of geochemical dissolution. In this work, we developed a machine learning framework to extract the important features that support mineralization in the form of dissolution. In addition, we use structural and topological features of the fracture network to predict the remaining quartz volume in quasi-steady state conditions. As a first step to characterizing carbon mineralization, we study dissolution with this framework. We studied a variety of reaction and fracture parameters and their impact on the dissolution of quartz in fracture networks. We found that the dissolution reaction rate constant of quartz and the distance to the flowing backbone in the fracture network are the two most important features that control the amount of quartz left in the system. For the first time, we use a combination of a finite-volume reservoir model and graph-based approach to study reactive transport in a complex fracture network to determine the key features that control dissolution.

Reconstruction of Fields from Sparse Sensing: Differentiable Sensor Placement Enhances Generalization

Recreating complex, high-dimensional global fields from limited data points is a grand challenge across various scientific and industrial domains. Given the prohibitive costs of specialized sensors and the frequent inaccessibility of certain regions of the domain, achieving full field coverage is typically not feasible. Therefore, the development of algorithms that intelligently improve sensor placement is of significant value. In this study, we introduce a general approach that employs differentiable programming to exploit sensor placement within the training of a neural network model in order to improve field reconstruction. We evaluated our method using two distinct datasets; the results show that our approach improved test scores. Ultimately, our method of differentiable placement strategies has the potential to significantly increase data collection efficiency, enable more thorough area coverage, and reduce redundancy in sensor deployment.

Progressive reduced order modeling: empowering data-driven modeling with selective knowledge transfer

Data-driven modeling can suffer from a constant demand for data, leading to reduced accuracy and impractical for engineering applications due to the high cost and scarcity of information. To address this challenge, we propose a progressive reduced order modeling framework that minimizes data cravings and enhances data-driven modeling's practicality. Our approach selectively transfers knowledge from previously trained models through gates, similar to how humans selectively use valuable knowledge while ignoring unuseful information. By filtering relevant information from previous models, we can create a surrogate model with minimal turnaround time and a smaller training set that can still achieve high accuracy. We have tested our framework in several cases, including transport in porous media, gravity-driven flow, and finite deformation in hyperelastic materials. Our results illustrate that retaining information from previous models and utilizing a valuable portion of that knowledge can significantly improve the accuracy of the current model. We have demonstrated the importance of progressive knowledge transfer and its impact on model accuracy with reduced training samples. For instance, our framework with four parent models outperforms the no-parent counterpart trained on data nine times larger. Our research unlocks data-driven modeling's potential for practical engineering applications by mitigating the data scarcity issue. Our proposed framework is a significant step toward more efficient and cost-effective data-driven modeling, fostering advancements across various fields.

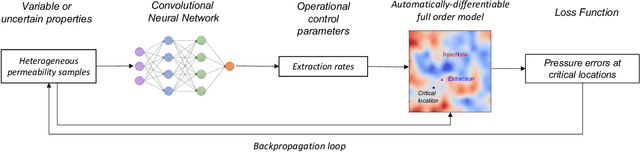
Physics-informed machine learning with differentiable programming for heterogeneous underground reservoir pressure management

Avoiding over-pressurization in subsurface reservoirs is critical for applications like CO2 sequestration and wastewater injection. Managing the pressures by controlling injection/extraction are challenging because of complex heterogeneity in the subsurface. The heterogeneity typically requires high-fidelity physics-based models to make predictions on CO$_2$ fate. Furthermore, characterizing the heterogeneity accurately is fraught with parametric uncertainty. Accounting for both, heterogeneity and uncertainty, makes this a computationally-intensive problem challenging for current reservoir simulators. To tackle this, we use differentiable programming with a full-physics model and machine learning to determine the fluid extraction rates that prevent over-pressurization at critical reservoir locations. We use DPFEHM framework, which has trustworthy physics based on the standard two-point flux finite volume discretization and is also automatically differentiable like machine learning models. Our physics-informed machine learning framework uses convolutional neural networks to learn an appropriate extraction rate based on the permeability field. We also perform a hyperparameter search to improve the model's accuracy. Training and testing scenarios are executed to evaluate the feasibility of using physics-informed machine learning to manage reservoir pressures. We constructed and tested a sufficiently accurate simulator that is 400000 times faster than the underlying physics-based simulator, allowing for near real-time analysis and robust uncertainty quantification.