Chun-Na Li
Learning using granularity statistical invariants for classification
Mar 29, 2024



Abstract:Learning using statistical invariants (LUSI) is a new learning paradigm, which adopts weak convergence mechanism, and can be applied to a wider range of classification problems. However, the computation cost of invariant matrices in LUSI is high for large-scale datasets during training. To settle this issue, this paper introduces a granularity statistical invariant for LUSI, and develops a new learning paradigm called learning using granularity statistical invariants (LUGSI). LUGSI employs both strong and weak convergence mechanisms, taking a perspective of minimizing expected risk. As far as we know, it is the first time to construct granularity statistical invariants. Compared to LUSI, the introduction of this new statistical invariant brings two advantages. Firstly, it enhances the structural information of the data. Secondly, LUGSI transforms a large invariant matrix into a smaller one by maximizing the distance between classes, achieving feasibility for large-scale datasets classification problems and significantly enhancing the training speed of model operations. Experimental results indicate that LUGSI not only exhibits improved generalization capabilities but also demonstrates faster training speed, particularly for large-scale datasets.
Nonlinear Kernel Support Vector Machine with 0-1 Soft Margin Loss
Mar 01, 2022
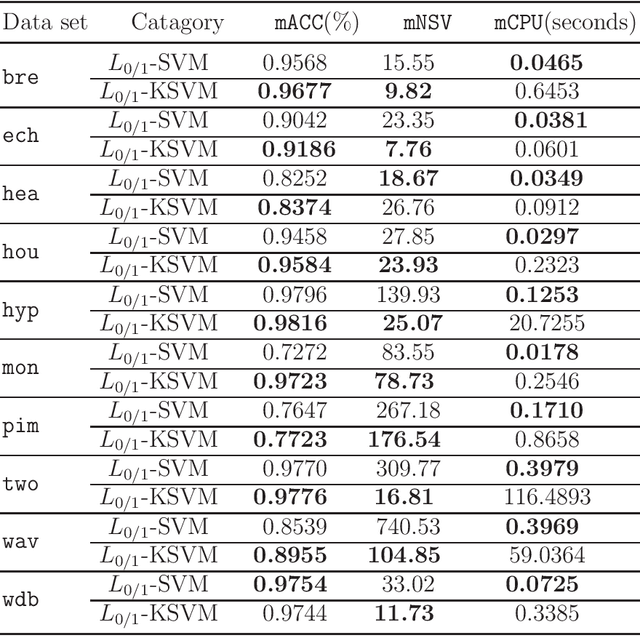
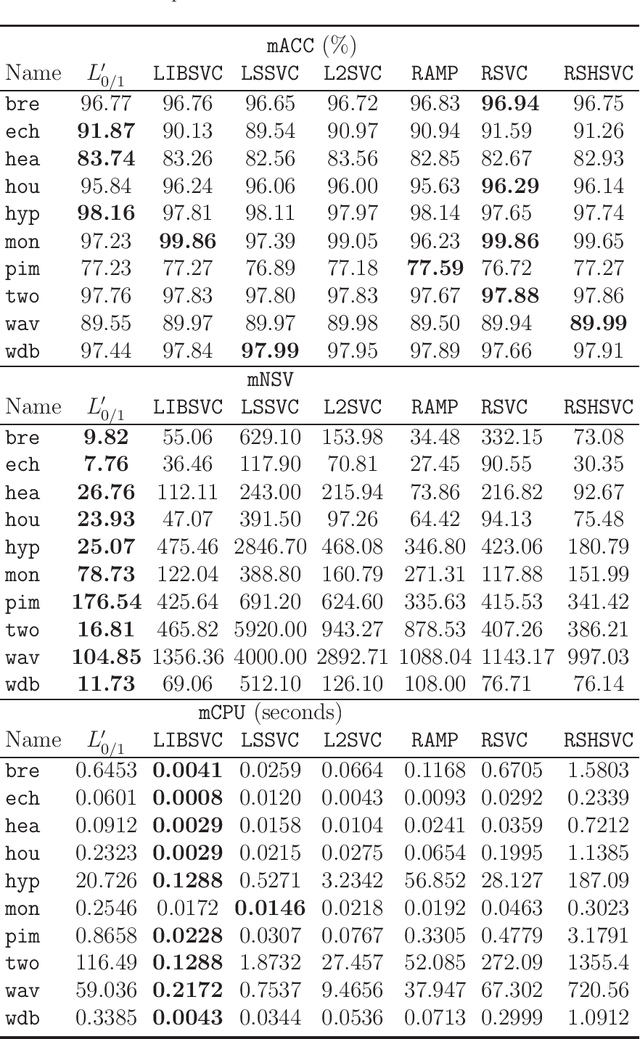
Abstract:Recent advance on linear support vector machine with the 0-1 soft margin loss ($L_{0/1}$-SVM) shows that the 0-1 loss problem can be solved directly. However, its theoretical and algorithmic requirements restrict us extending the linear solving framework to its nonlinear kernel form directly, the absence of explicit expression of Lagrangian dual function of $L_{0/1}$-SVM is one big deficiency among of them. In this paper, by applying the nonparametric representation theorem, we propose a nonlinear model for support vector machine with 0-1 soft margin loss, called $L_{0/1}$-KSVM, which cunningly involves the kernel technique into it and more importantly, follows the success on systematically solving its linear task. Its optimal condition is explored theoretically and a working set selection alternating direction method of multipliers (ADMM) algorithm is introduced to acquire its numerical solution. Moreover, we firstly present a closed-form definition to the support vector (SV) of $L_{0/1}$-KSVM. Theoretically, we prove that all SVs of $L_{0/1}$-KSVM are only located on the parallel decision surfaces. The experiment part also shows that $L_{0/1}$-KSVM has much fewer SVs, simultaneously with a decent predicting accuracy, when comparing to its linear peer $L_{0/1}$-SVM and the other six nonlinear benchmark SVM classifiers.
Two-dimensional Bhattacharyya bound linear discriminant analysis with its applications
Nov 11, 2020

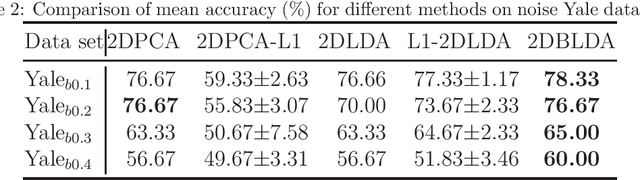
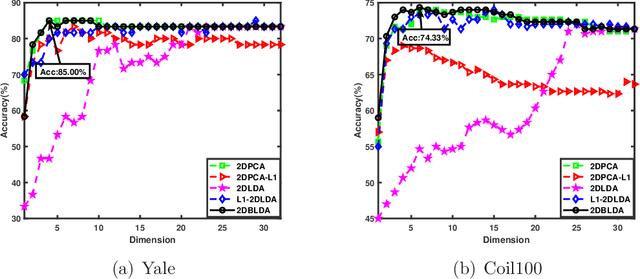
Abstract:Recently proposed L2-norm linear discriminant analysis criterion via the Bhattacharyya error bound estimation (L2BLDA) is an effective improvement of linear discriminant analysis (LDA) for feature extraction. However, L2BLDA is only proposed to cope with vector input samples. When facing with two-dimensional (2D) inputs, such as images, it will lose some useful information, since it does not consider intrinsic structure of images. In this paper, we extend L2BLDA to a two-dimensional Bhattacharyya bound linear discriminant analysis (2DBLDA). 2DBLDA maximizes the matrix-based between-class distance which is measured by the weighted pairwise distances of class means and meanwhile minimizes the matrix-based within-class distance. The weighting constant between the between-class and within-class terms is determined by the involved data that makes the proposed 2DBLDA adaptive. In addition, the criterion of 2DBLDA is equivalent to optimizing an upper bound of the Bhattacharyya error. The construction of 2DBLDA makes it avoid the small sample size problem while also possess robustness, and can be solved through a simple standard eigenvalue decomposition problem. The experimental results on image recognition and face image reconstruction demonstrate the effectiveness of the proposed methods.
Capped norm linear discriminant analysis and its applications
Nov 04, 2020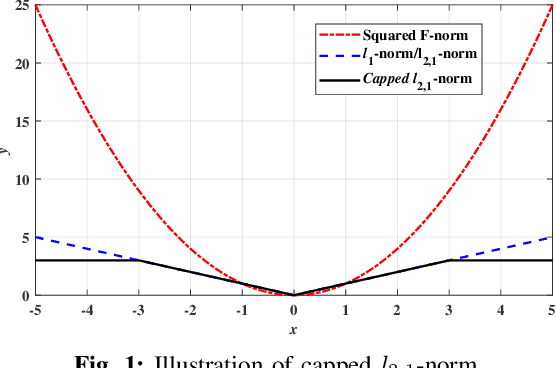
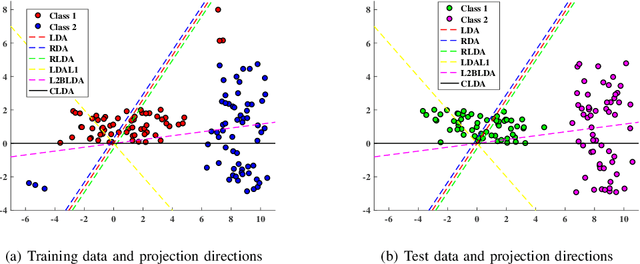
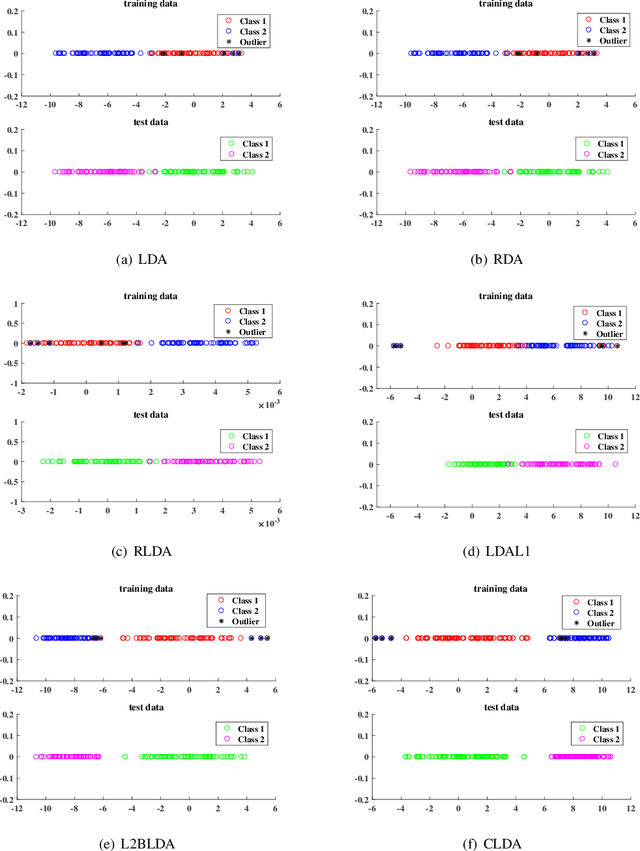
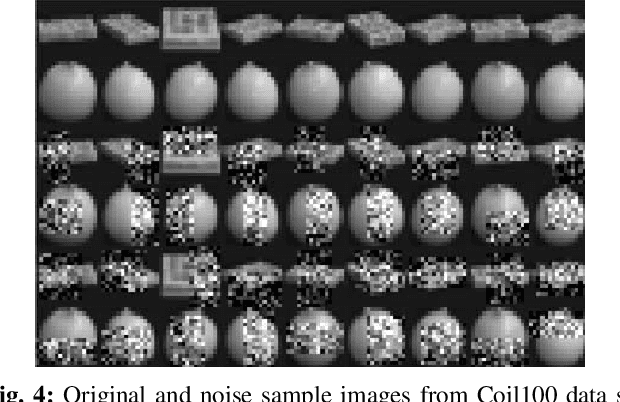
Abstract:Classical linear discriminant analysis (LDA) is based on squared Frobenious norm and hence is sensitive to outliers and noise. To improve the robustness of LDA, in this paper, we introduce capped l_{2,1}-norm of a matrix, which employs non-squared l_2-norm and "capped" operation, and further propose a novel capped l_{2,1}-norm linear discriminant analysis, called CLDA. Due to the use of capped l_{2,1}-norm, CLDA can effectively remove extreme outliers and suppress the effect of noise data. In fact, CLDA can be also viewed as a weighted LDA. CLDA is solved through a series of generalized eigenvalue problems with theoretical convergency. The experimental results on an artificial data set, some UCI data sets and two image data sets demonstrate the effectiveness of CLDA.
Principal Component Analysis Based on T$\ell_1$-norm Maximization
May 23, 2020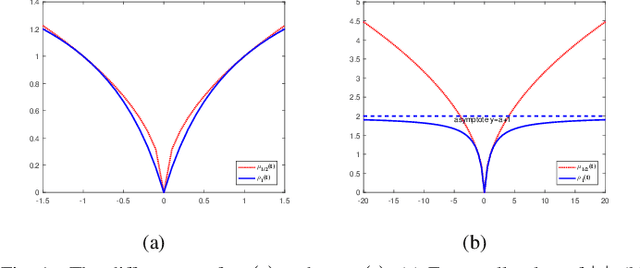
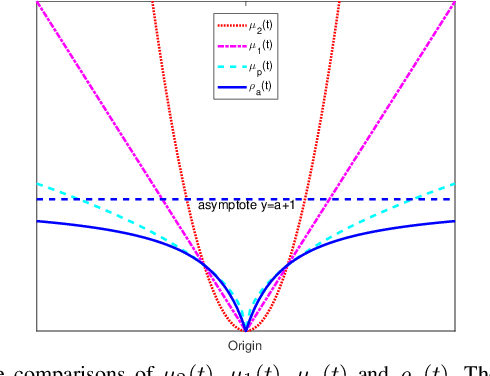
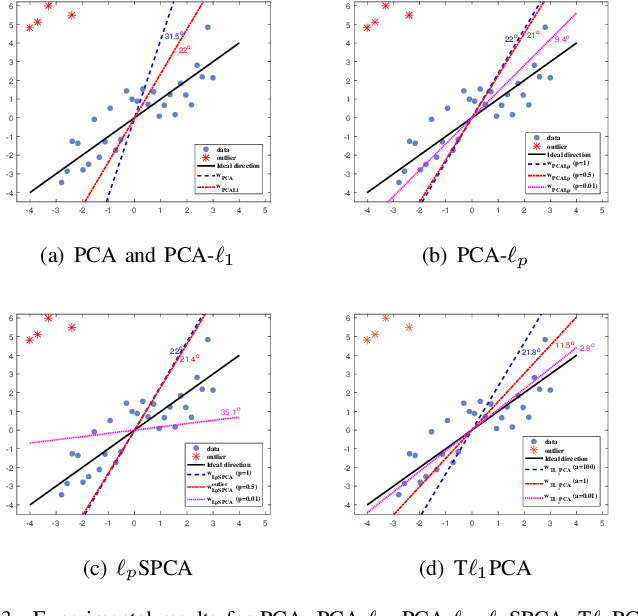
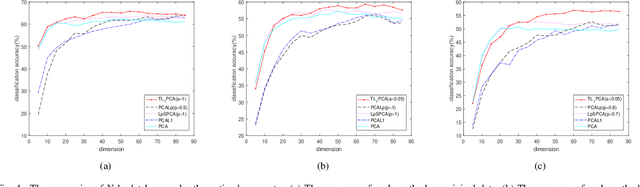
Abstract:Classical principal component analysis (PCA) may suffer from the sensitivity to outliers and noise. Therefore PCA based on $\ell_1$-norm and $\ell_p$-norm ($0 < p < 1$) have been studied. Among them, the ones based on $\ell_p$-norm seem to be most interesting from the robustness point of view. However, their numerical performance is not satisfactory. Note that, although T$\ell_1$-norm is similar to $\ell_p$-norm ($0 < p < 1$) in some sense, it has the stronger suppression effect to outliers and better continuity. So PCA based on T$\ell_1$-norm is proposed in this paper. Our numerical experiments have shown that its performance is superior than PCA-$\ell_p$ and $\ell_p$SPCA as well as PCA, PCA-$\ell_1$ obviously.
Single Versus Union: Non-parallel Support Vector Machine Frameworks
Oct 22, 2019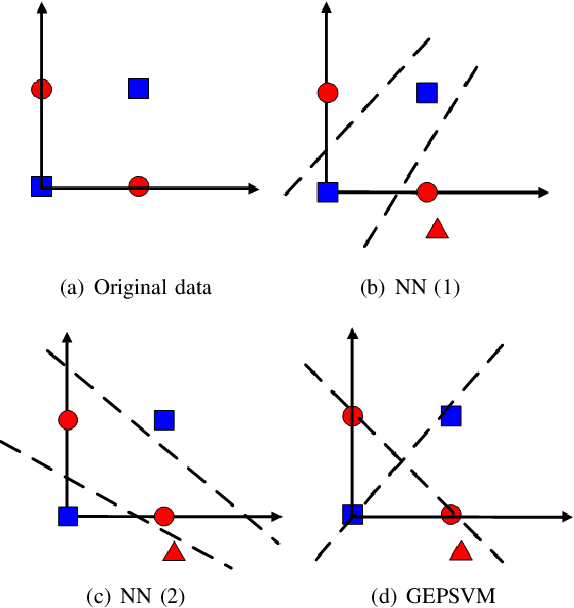

Abstract:Considering the classification problem, we summarize the nonparallel support vector machines with the nonparallel hyperplanes to two types of frameworks. The first type constructs the hyperplanes separately. It solves a series of small optimization problems to obtain a series of hyperplanes, but is hard to measure the loss of each sample. The other type constructs all the hyperplanes simultaneously, and it solves one big optimization problem with the ascertained loss of each sample. We give the characteristics of each framework and compare them carefully. In addition, based on the second framework, we construct a max-min distance-based nonparallel support vector machine for multiclass classification problem, called NSVM. It constructs hyperplanes with large distance margin by solving an optimization problem. Experimental results on benchmark data sets and human face databases show the advantages of our NSVM.
A general model for plane-based clustering with loss function
Jan 26, 2019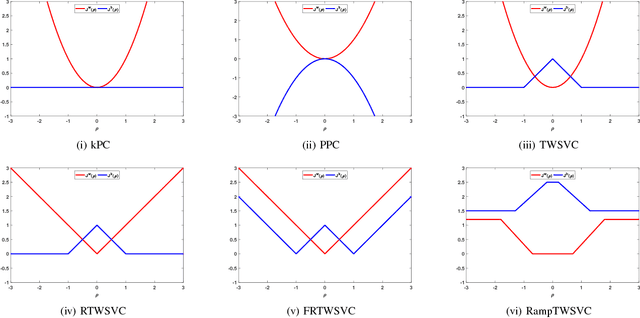
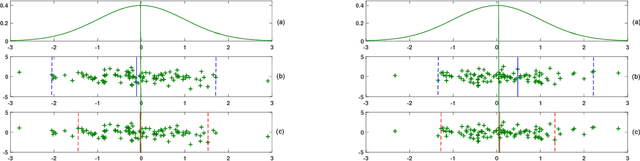
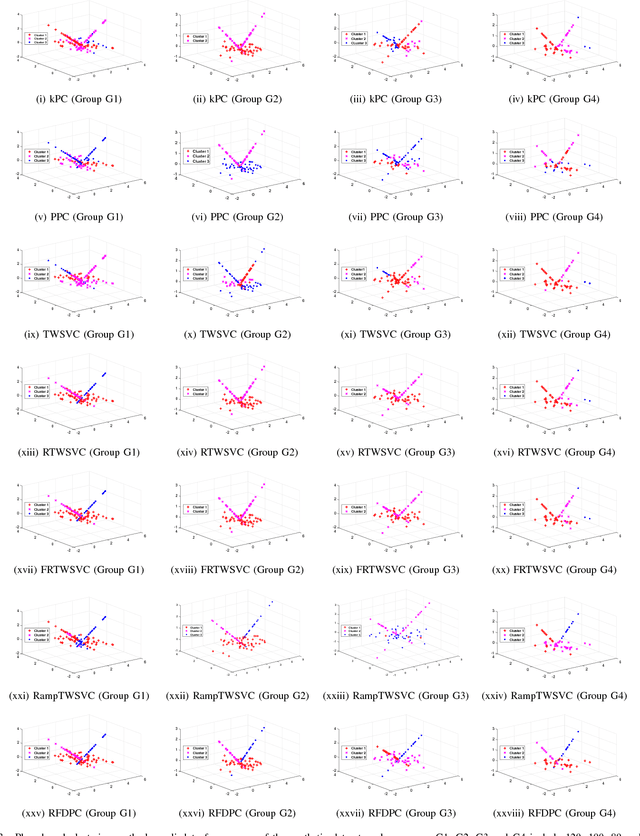
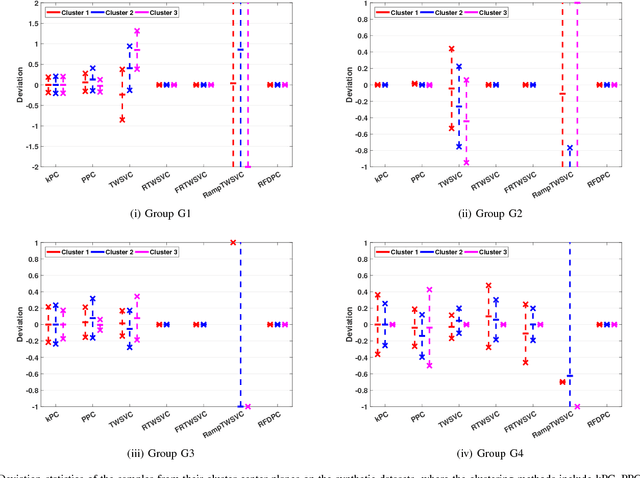
Abstract:In this paper, we propose a general model for plane-based clustering. The general model contains many existing plane-based clustering methods, e.g., k-plane clustering (kPC), proximal plane clustering (PPC), twin support vector clustering (TWSVC) and its extensions. Under this general model, one may obtain an appropriate clustering method for specific purpose. The general model is a procedure corresponding to an optimization problem, where the optimization problem minimizes the total loss of the samples. Thereinto, the loss of a sample derives from both within-cluster and between-cluster. In theory, the termination conditions are discussed, and we prove that the general model terminates in a finite number of steps at a local or weak local optimal point. Furthermore, based on this general model, we propose a plane-based clustering method by introducing a new loss function to capture the data distribution precisely. Experimental results on artificial and public available datasets verify the effectiveness of the proposed method.
Ramp-based Twin Support Vector Clustering
Dec 10, 2018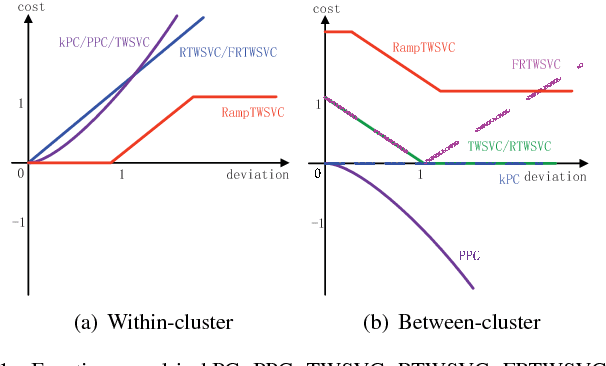
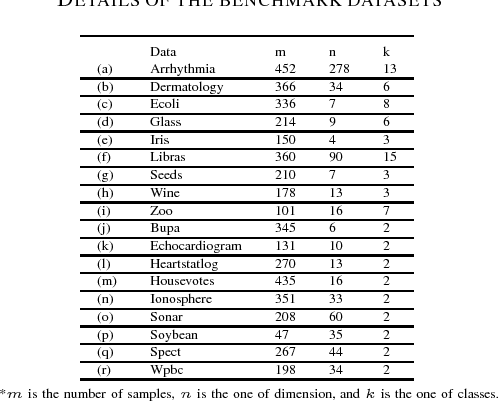
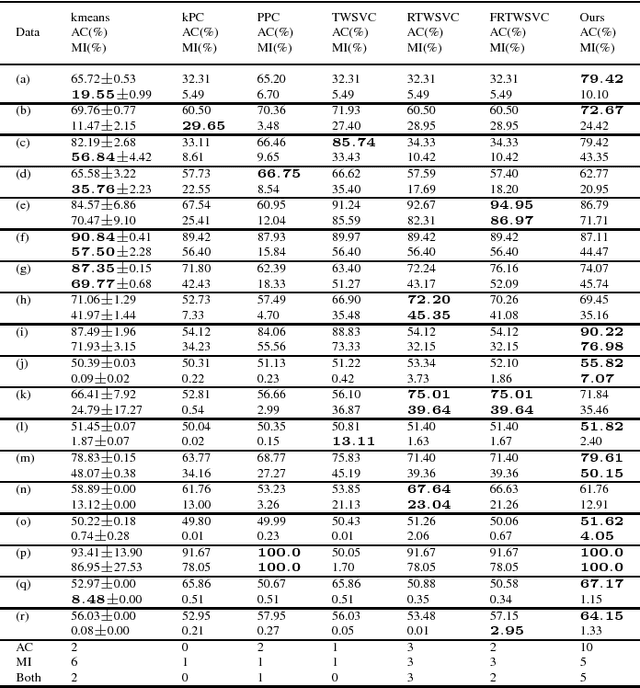
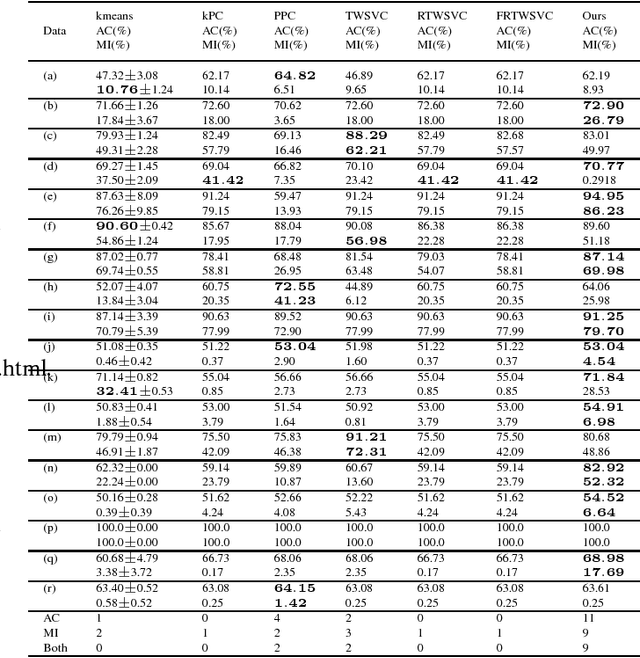
Abstract:Traditional plane-based clustering methods measure the cost of within-cluster and between-cluster by quadratic, linear or some other unbounded functions, which may amplify the impact of cost. This letter introduces a ramp cost function into the plane-based clustering to propose a new clustering method, called ramp-based twin support vector clustering (RampTWSVC). RampTWSVC is more robust because of its boundness, and thus it is more easier to find the intrinsic clusters than other plane-based clustering methods. The non-convex programming problem in RampTWSVC is solved efficiently through an alternating iteration algorithm, and its local solution can be obtained in a finite number of iterations theoretically. In addition, the nonlinear manifold-based formation of RampTWSVC is also proposed by kernel trick. Experimental results on several benchmark datasets show the better performance of our RampTWSVC compared with other plane-based clustering methods.
Robust Bhattacharyya bound linear discriminant analysis through adaptive algorithm
Nov 06, 2018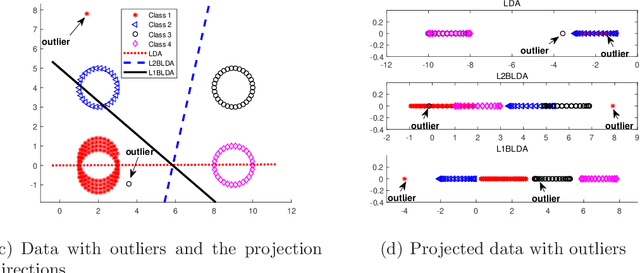
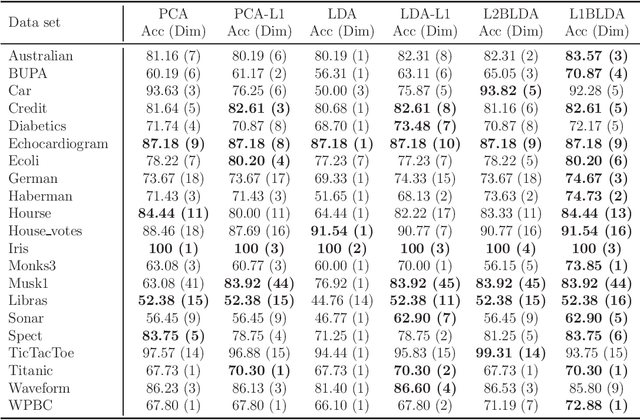
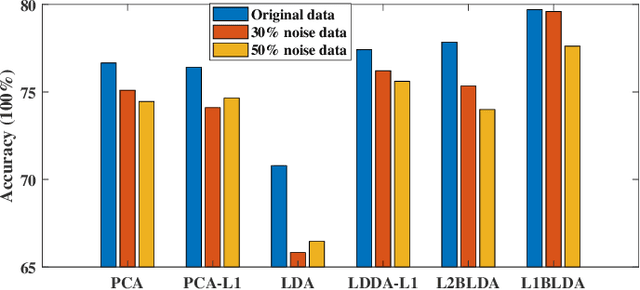
Abstract:In this paper, we propose a novel linear discriminant analysis criterion via the Bhattacharyya error bound estimation based on a novel L1-norm (L1BLDA) and L2-norm (L2BLDA). Both L1BLDA and L2BLDA maximize the between-class scatters which are measured by the weighted pairwise distances of class means and meanwhile minimize the within-class scatters under the L1-norm and L2-norm, respectively. The proposed models can avoid the small sample size (SSS) problem and have no rank limit that may encounter in LDA. It is worth mentioning that, the employment of L1-norm gives a robust performance of L1BLDA, and L1BLDA is solved through an effective non-greedy alternating direction method of multipliers (ADMM), where all the projection vectors can be obtained once for all. In addition, the weighting constants of L1BLDA and L2BLDA between the between-class and within-class terms are determined by the involved data set, which makes our L1BLDA and L2BLDA adaptive. The experimental results on both benchmark data sets as well as the handwritten digit databases demonstrate the effectiveness of the proposed methods.
Generalized two-dimensional linear discriminant analysis with regularization
Oct 25, 2018


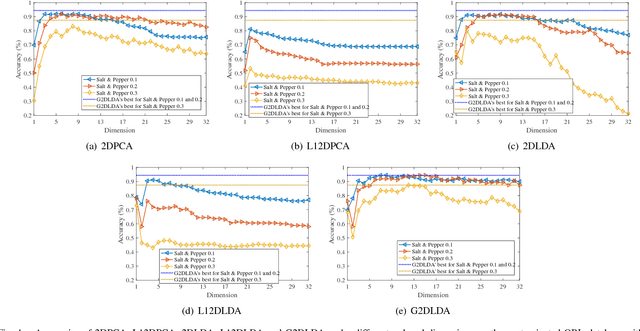
Abstract:Recent advances show that two-dimensional linear discriminant analysis (2DLDA) is a successful matrix based dimensionality reduction method. However, 2DLDA may encounter the singularity issue theoretically and the sensitivity to outliers. In this paper, a generalized Lp-norm 2DLDA framework with regularization for an arbitrary $p>0$ is proposed, named G2DLDA. There are mainly two contributions of G2DLDA: one is G2DLDA model uses an arbitrary Lp-norm to measure the between-class and within-class scatter, and hence a proper $p$ can be selected to achieve the robustness. The other one is that by introducing an extra regularization term, G2DLDA achieves better generalization performance, and solves the singularity problem. In addition, G2DLDA can be solved through a series of convex problems with equality constraint, and it has closed solution for each single problem. Its convergence can be guaranteed theoretically when $1\leq p\leq2$. Preliminary experimental results on three contaminated human face databases show the effectiveness of the proposed G2DLDA.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge