Snorkel DryBell: A Case Study in Deploying Weak Supervision at Industrial Scale

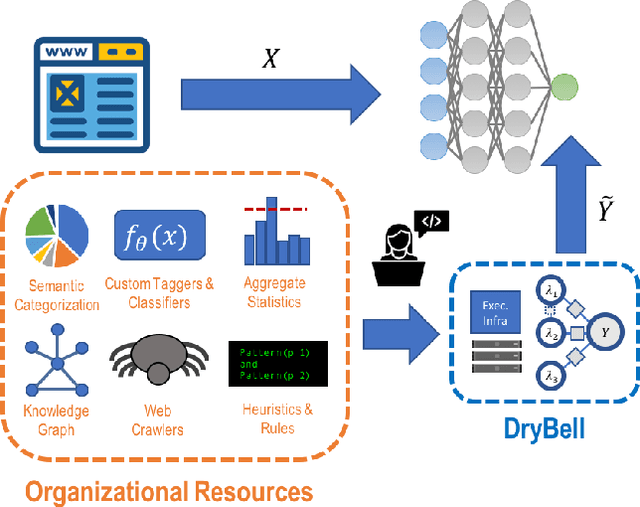
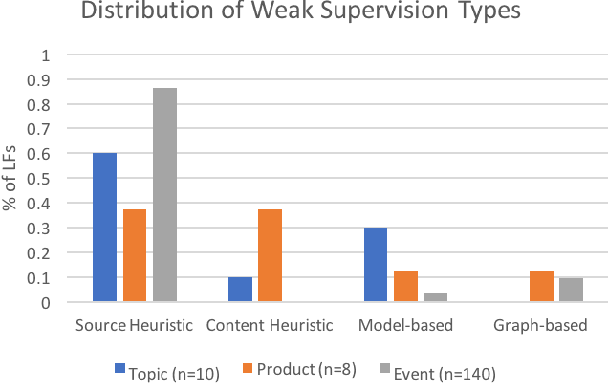
Labeling training data is one of the most costly bottlenecks in developing or modifying machine learning-based applications. We survey how resources from across an organization can be used as weak supervision sources for three classification tasks at Google, in order to bring development time and cost down by an order of magnitude. We build on the Snorkel framework, extending it as a new system, Snorkel DryBell, which integrates with Google's distributed production systems and enables engineers to develop and execute weak supervision strategies over millions of examples in less than thirty minutes. We find that Snorkel DryBell creates classifiers of comparable quality to ones trained using up to tens of thousands of hand-labeled examples, in part by leveraging organizational resources not servable in production which contribute an average 52% performance improvement to the weakly supervised classifiers.

Low-Precision Random Fourier Features for Memory-Constrained Kernel Approximation

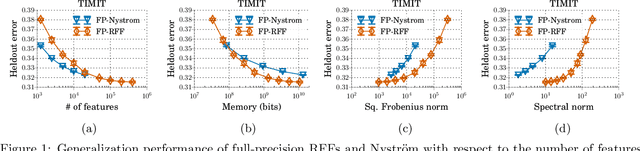
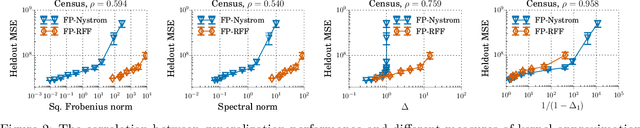
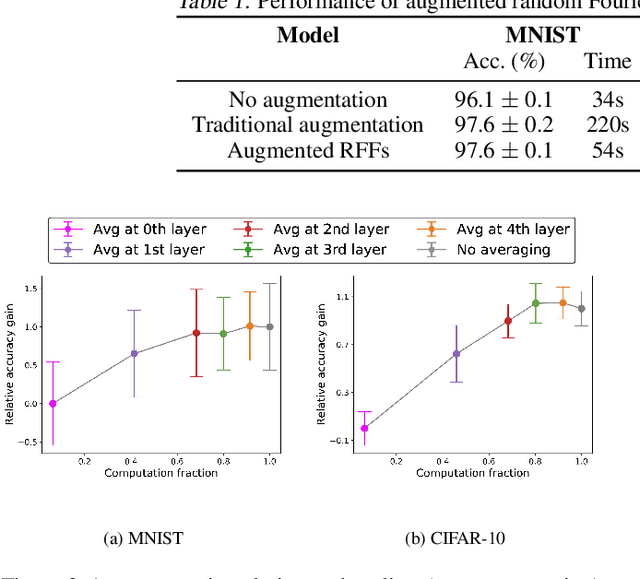
We investigate how to train kernel approximation methods that generalize well under a memory budget. Building on recent theoretical work, we define a measure of kernel approximation error which we find to be much more predictive of the empirical generalization performance of kernel approximation methods than conventional metrics. An important consequence of this definition is that a kernel approximation matrix must be high-rank to attain close approximation. Because storing a high-rank approximation is memory-intensive, we propose using a low-precision quantization of random Fourier features (LP-RFFs) to build a high-rank approximation under a memory budget. Theoretically, we show quantization has a negligible effect on generalization performance in important settings. Empirically, we demonstrate across four benchmark datasets that LP-RFFs can match the performance of full-precision RFFs and the Nystr\"{o}m method, with 3x-10x and 50x-460x less memory, respectively.

Training Classifiers with Natural Language Explanations

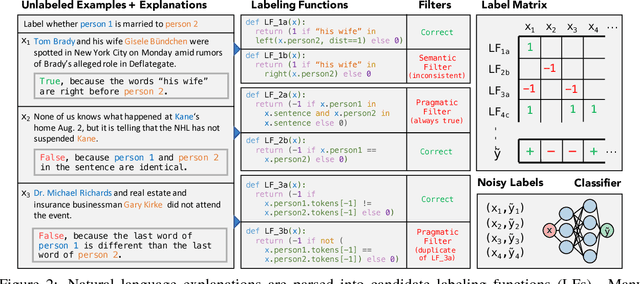
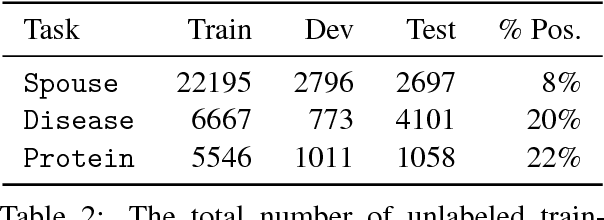
Training accurate classifiers requires many labels, but each label provides only limited information (one bit for binary classification). In this work, we propose BabbleLabble, a framework for training classifiers in which an annotator provides a natural language explanation for each labeling decision. A semantic parser converts these explanations into programmatic labeling functions that generate noisy labels for an arbitrary amount of unlabeled data, which is used to train a classifier. On three relation extraction tasks, we find that users are able to train classifiers with comparable F1 scores from 5-100$\times$ faster by providing explanations instead of just labels. Furthermore, given the inherent imperfection of labeling functions, we find that a simple rule-based semantic parser suffices.

Hypertree Decompositions Revisited for PGMs

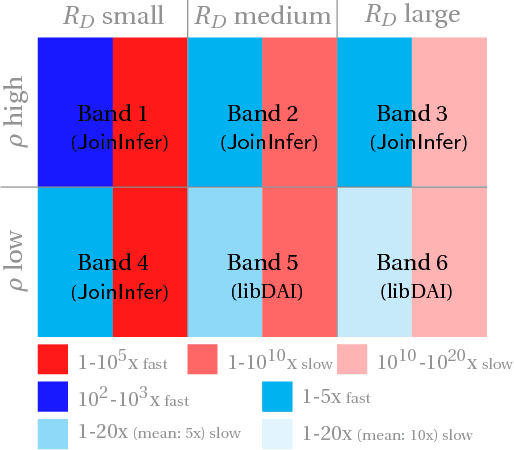
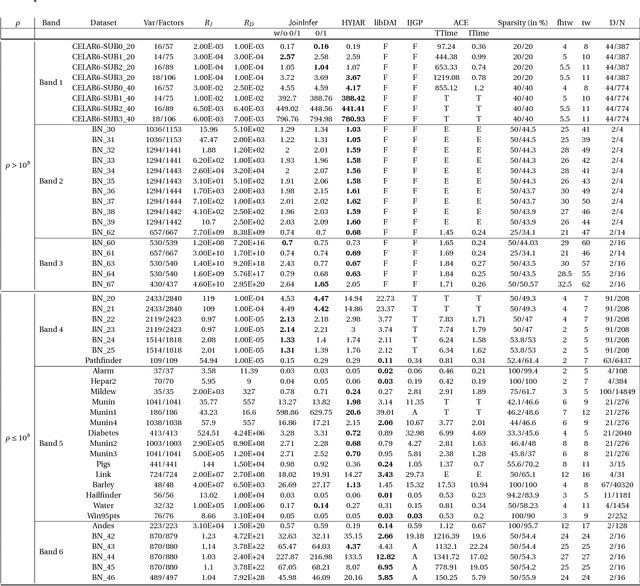
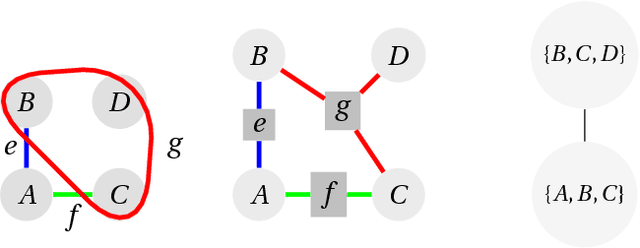
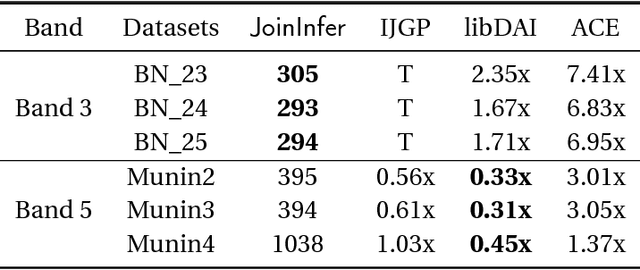
We revisit the classical problem of exact inference on probabilistic graphical models (PGMs). Our algorithm is based on recent \emph{worst-case optimal database join} algorithms, which can be asymptotically faster than traditional data processing methods. We present the first empirical evaluation of these algorithms via JoinInfer -- a new exact inference engine. We empirically explore the properties of the data for which our engine can be expected to outperform traditional inference engines, refining current theoretical notions. Further, JoinInfer outperforms existing state-of-the-art inference engines (ACE, IJGP and libDAI) on some standard benchmark datasets by up to a factor of 630x. Finally, we propose a promising data-driven heuristic that extends JoinInfer to automatically tailor its parameters and/or switch to the traditional inference algorithms.

Representation Tradeoffs for Hyperbolic Embeddings

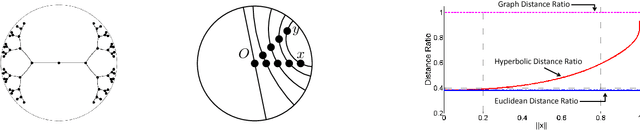
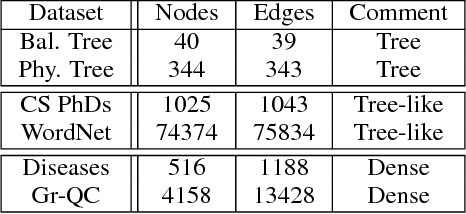
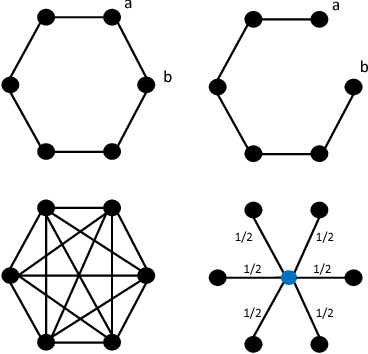
Hyperbolic embeddings offer excellent quality with few dimensions when embedding hierarchical data structures like synonym or type hierarchies. Given a tree, we give a combinatorial construction that embeds the tree in hyperbolic space with arbitrarily low distortion without using optimization. On WordNet, our combinatorial embedding obtains a mean-average-precision of 0.989 with only two dimensions, while Nickel et al.'s recent construction obtains 0.87 using 200 dimensions. We provide upper and lower bounds that allow us to characterize the precision-dimensionality tradeoff inherent in any hyperbolic embedding. To embed general metric spaces, we propose a hyperbolic generalization of multidimensional scaling (h-MDS). We show how to perform exact recovery of hyperbolic points from distances, provide a perturbation analysis, and give a recovery result that allows us to reduce dimensionality. The h-MDS approach offers consistently low distortion even with few dimensions across several datasets. Finally, we extract lessons from the algorithms and theory above to design a PyTorch-based implementation that can handle incomplete information and is scalable.

A Kernel Theory of Modern Data Augmentation

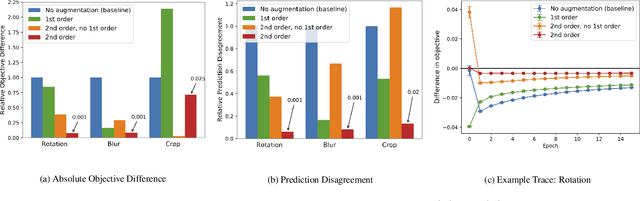
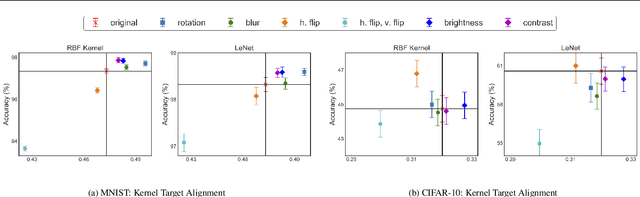
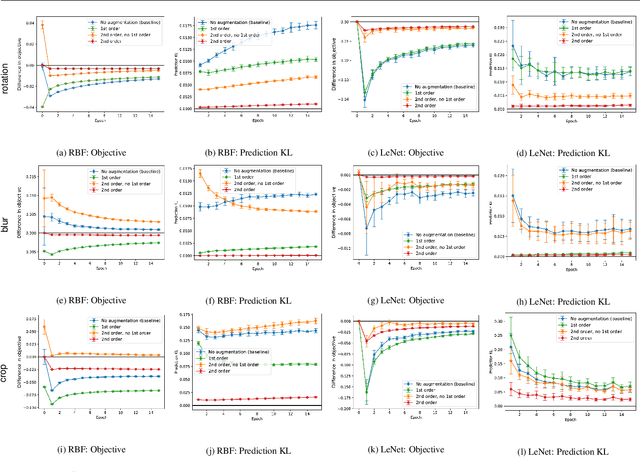
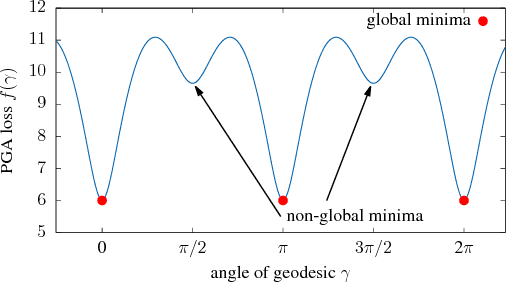
Data augmentation, a technique in which a training set is expanded with class-preserving transformations, is ubiquitous in modern machine learning pipelines. In this paper, we seek to establish a theoretical framework for understanding modern data augmentation techniques. We start by showing that for kernel classifiers, data augmentation can be approximated by first-order feature averaging and second-order variance regularization components. We connect this general approximation framework to prior work in invariant kernels, tangent propagation, and robust optimization. Next, we explicitly tackle the compositional aspect of modern data augmentation techniques, proposing a novel model of data augmentation as a Markov process. Under this model, we show that performing $k$-nearest neighbors with data augmentation is asymptotically equivalent to a kernel classifier. Finally, we illustrate ways in which our theoretical framework can be leveraged to accelerate machine learning workflows in practice, including reducing the amount of computation needed to train on augmented data, and predicting the utility of a transformation prior to training.

High-Accuracy Low-Precision Training

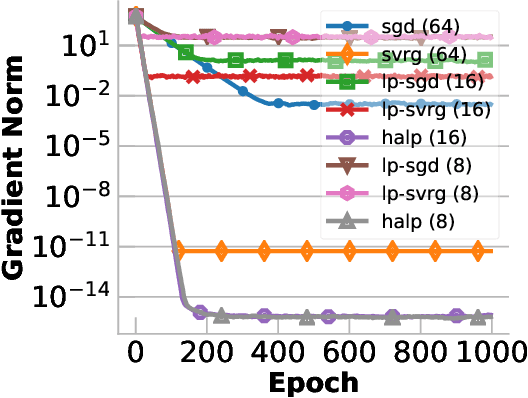
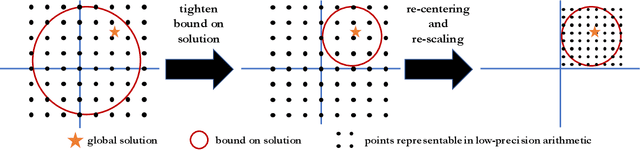
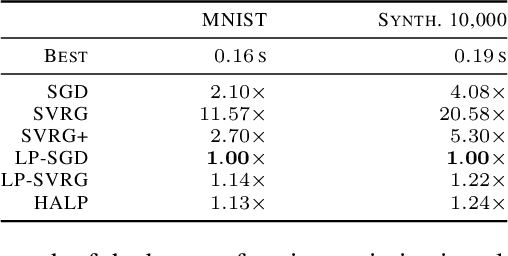
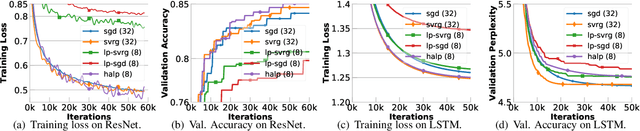
Low-precision computation is often used to lower the time and energy cost of machine learning, and recently hardware accelerators have been developed to support it. Still, it has been used primarily for inference - not training. Previous low-precision training algorithms suffered from a fundamental tradeoff: as the number of bits of precision is lowered, quantization noise is added to the model, which limits statistical accuracy. To address this issue, we describe a simple low-precision stochastic gradient descent variant called HALP. HALP converges at the same theoretical rate as full-precision algorithms despite the noise introduced by using low precision throughout execution. The key idea is to use SVRG to reduce gradient variance, and to combine this with a novel technique called bit centering to reduce quantization error. We show that on the CPU, HALP can run up to $4 \times$ faster than full-precision SVRG and can match its convergence trajectory. We implemented HALP in TensorQuant, and show that it exceeds the validation performance of plain low-precision SGD on two deep learning tasks.

Gaussian Quadrature for Kernel Features

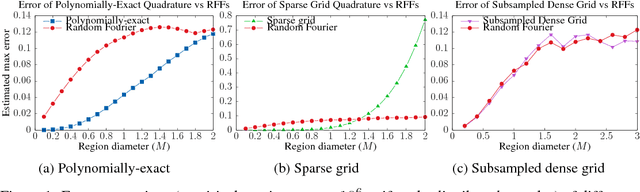
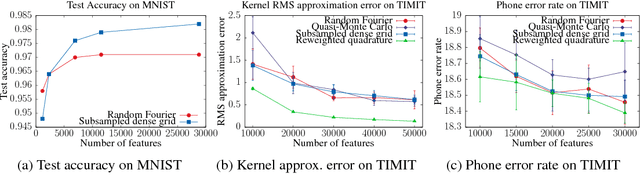
Kernel methods have recently attracted resurgent interest, showing performance competitive with deep neural networks in tasks such as speech recognition. The random Fourier features map is a technique commonly used to scale up kernel machines, but employing the randomized feature map means that $O(\epsilon^{-2})$ samples are required to achieve an approximation error of at most $\epsilon$. We investigate some alternative schemes for constructing feature maps that are deterministic, rather than random, by approximating the kernel in the frequency domain using Gaussian quadrature. We show that deterministic feature maps can be constructed, for any $\gamma > 0$, to achieve error $\epsilon$ with $O(e^{e^\gamma} + \epsilon^{-1/\gamma})$ samples as $\epsilon$ goes to 0. Our method works particularly well with sparse ANOVA kernels, which are inspired by the convolutional layer of CNNs. We validate our methods on datasets in different domains, such as MNIST and TIMIT, showing that deterministic features are faster to generate and achieve accuracy comparable to the state-of-the-art kernel methods based on random Fourier features.

Snorkel: Rapid Training Data Creation with Weak Supervision

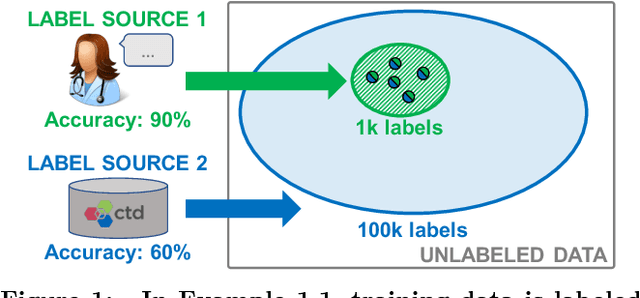
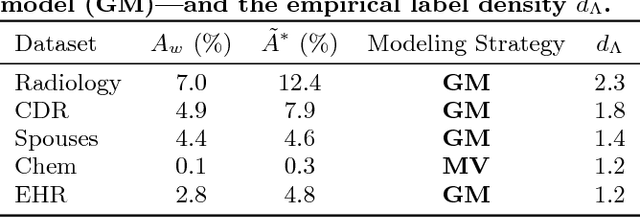
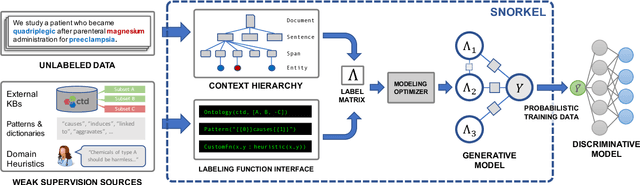
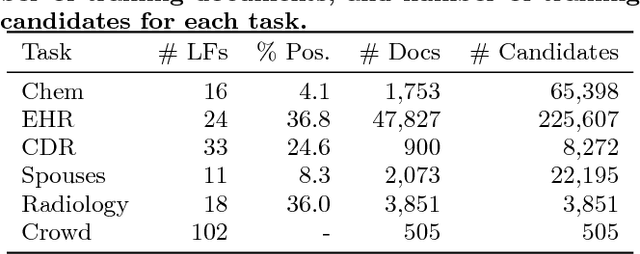
Labeling training data is increasingly the largest bottleneck in deploying machine learning systems. We present Snorkel, a first-of-its-kind system that enables users to train state-of-the-art models without hand labeling any training data. Instead, users write labeling functions that express arbitrary heuristics, which can have unknown accuracies and correlations. Snorkel denoises their outputs without access to ground truth by incorporating the first end-to-end implementation of our recently proposed machine learning paradigm, data programming. We present a flexible interface layer for writing labeling functions based on our experience over the past year collaborating with companies, agencies, and research labs. In a user study, subject matter experts build models 2.8x faster and increase predictive performance an average 45.5% versus seven hours of hand labeling. We study the modeling tradeoffs in this new setting and propose an optimizer for automating tradeoff decisions that gives up to 1.8x speedup per pipeline execution. In two collaborations, with the U.S. Department of Veterans Affairs and the U.S. Food and Drug Administration, and on four open-source text and image data sets representative of other deployments, Snorkel provides 132% average improvements to predictive performance over prior heuristic approaches and comes within an average 3.60% of the predictive performance of large hand-curated training sets.

Learning to Compose Domain-Specific Transformations for Data Augmentation

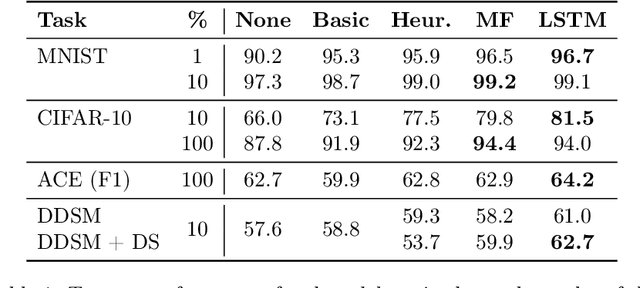
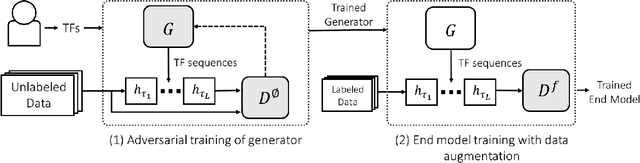
Data augmentation is a ubiquitous technique for increasing the size of labeled training sets by leveraging task-specific data transformations that preserve class labels. While it is often easy for domain experts to specify individual transformations, constructing and tuning the more sophisticated compositions typically needed to achieve state-of-the-art results is a time-consuming manual task in practice. We propose a method for automating this process by learning a generative sequence model over user-specified transformation functions using a generative adversarial approach. Our method can make use of arbitrary, non-deterministic transformation functions, is robust to misspecified user input, and is trained on unlabeled data. The learned transformation model can then be used to perform data augmentation for any end discriminative model. In our experiments, we show the efficacy of our approach on both image and text datasets, achieving improvements of 4.0 accuracy points on CIFAR-10, 1.4 F1 points on the ACE relation extraction task, and 3.4 accuracy points when using domain-specific transformation operations on a medical imaging dataset as compared to standard heuristic augmentation approaches.