On the Byzantine-Resilience of Distillation-Based Federated Learning

Federated Learning (FL) algorithms using Knowledge Distillation (KD) have received increasing attention due to their favorable properties with respect to privacy, non-i.i.d. data and communication cost. These methods depart from transmitting model parameters and, instead, communicate information about a learning task by sharing predictions on a public dataset. In this work, we study the performance of such approaches in the byzantine setting, where a subset of the clients act in an adversarial manner aiming to disrupt the learning process. We show that KD-based FL algorithms are remarkably resilient and analyze how byzantine clients can influence the learning process compared to Federated Averaging. Based on these insights, we introduce two new byzantine attacks and demonstrate that they are effective against prior byzantine-resilient methods. Additionally, we propose FilterExp, a novel method designed to enhance the byzantine resilience of KD-based FL algorithms and demonstrate its efficacy. Finally, we provide a general method to make attacks harder to detect, improving their effectiveness.

Accelerated Methods for Riemannian Min-Max Optimization Ensuring Bounded Geometric Penalties

In this work, we study optimization problems of the form $\min_x \max_y f(x, y)$, where $f(x, y)$ is defined on a product Riemannian manifold $\mathcal{M} \times \mathcal{N}$ and is $\mu_x$-strongly geodesically convex (g-convex) in $x$ and $\mu_y$-strongly g-concave in $y$, for $\mu_x, \mu_y \geq 0$. We design accelerated methods when $f$ is $(L_x, L_y, L_{xy})$-smooth and $\mathcal{M}$, $\mathcal{N}$ are Hadamard. To that aim we introduce new g-convex optimization results, of independent interest: we show global linear convergence for metric-projected Riemannian gradient descent and improve existing accelerated methods by reducing geometric constants. Additionally, we complete the analysis of two previous works applying to the Riemannian min-max case by removing an assumption about iterates staying in a pre-specified compact set.

Efficient Online-Bandit Strategies for Minimax Learning Problems

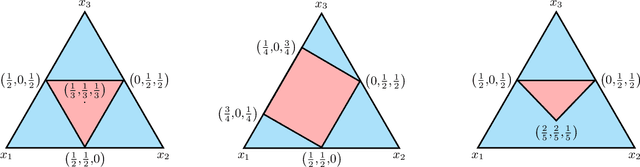
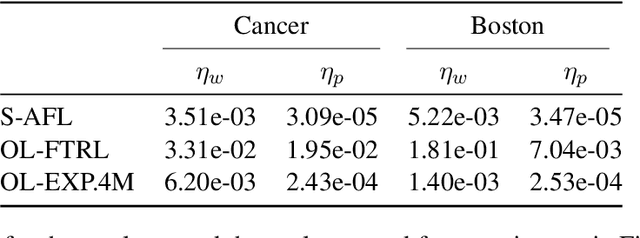
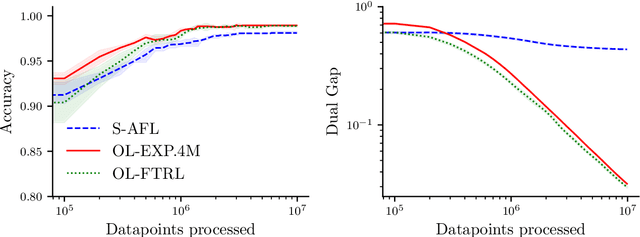
Several learning problems involve solving min-max problems, e.g., empirical distributional robust learning or learning with non-standard aggregated losses. More specifically, these problems are convex-linear problems where the minimization is carried out over the model parameters $w\in\mathcal{W}$ and the maximization over the empirical distribution $p\in\mathcal{K}$ of the training set indexes, where $\mathcal{K}$ is the simplex or a subset of it. To design efficient methods, we let an online learning algorithm play against a (combinatorial) bandit algorithm. We argue that the efficiency of such approaches critically depends on the structure of $\mathcal{K}$ and propose two properties of $\mathcal{K}$ that facilitate designing efficient algorithms. We focus on a specific family of sets $\mathcal{S}_{n,k}$ encompassing various learning applications and provide high-probability convergence guarantees to the minimax values.

Linear Bandits on Uniformly Convex Sets

Linear bandit algorithms yield $\tilde{\mathcal{O}}(n\sqrt{T})$ pseudo-regret bounds on compact convex action sets $\mathcal{K}\subset\mathbb{R}^n$ and two types of structural assumptions lead to better pseudo-regret bounds. When $\mathcal{K}$ is the simplex or an $\ell_p$ ball with $p\in]1,2]$, there exist bandits algorithms with $\tilde{\mathcal{O}}(\sqrt{nT})$ pseudo-regret bounds. Here, we derive bandit algorithms for some strongly convex sets beyond $\ell_p$ balls that enjoy pseudo-regret bounds of $\tilde{\mathcal{O}}(\sqrt{nT})$, which answers an open question from [BCB12, \S 5.5.]. Interestingly, when the action set is uniformly convex but not necessarily strongly convex, we obtain pseudo-regret bounds with a dimension dependency smaller than $\mathcal{O}(\sqrt{n})$. However, this comes at the expense of asymptotic rates in $T$ varying between $\tilde{\mathcal{O}}(\sqrt{T})$ and $\tilde{\mathcal{O}}(T)$.