Linear Convergence of the Frank-Wolfe Algorithm over Product Polytopes

We study the linear convergence of Frank-Wolfe algorithms over product polytopes. We analyze two condition numbers for the product polytope, namely the \emph{pyramidal width} and the \emph{vertex-facet distance}, based on the condition numbers of individual polytope components. As a result, for convex objectives that are $\mu$-Polyak-{\L}ojasiewicz, we show linear convergence rates quantified in terms of the resulting condition numbers. We apply our results to the problem of approximately finding a feasible point in a polytope intersection in high-dimensions, and demonstrate the practical efficiency of our algorithms through empirical results.

Approximating Latent Manifolds in Neural Networks via Vanishing Ideals

Deep neural networks have reshaped modern machine learning by learning powerful latent representations that often align with the manifold hypothesis: high-dimensional data lie on lower-dimensional manifolds. In this paper, we establish a connection between manifold learning and computational algebra by demonstrating how vanishing ideals can characterize the latent manifolds of deep networks. To that end, we propose a new neural architecture that (i) truncates a pretrained network at an intermediate layer, (ii) approximates each class manifold via polynomial generators of the vanishing ideal, and (iii) transforms the resulting latent space into linearly separable features through a single polynomial layer. The resulting models have significantly fewer layers than their pretrained baselines, while maintaining comparable accuracy, achieving higher throughput, and utilizing fewer parameters. Furthermore, drawing on spectral complexity analysis, we derive sharper theoretical guarantees for generalization, showing that our approach can in principle offer tighter bounds than standard deep networks. Numerical experiments confirm the effectiveness and efficiency of the proposed approach.

Approximate Vanishing Ideal Computations at Scale

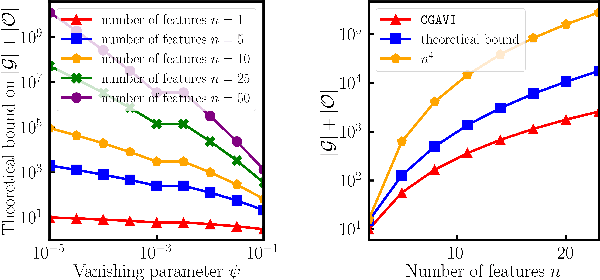
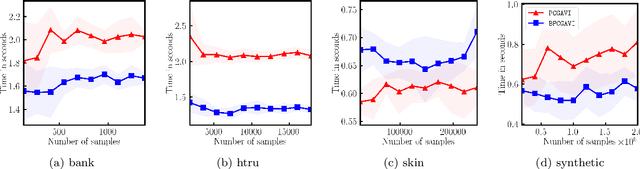
The approximate vanishing ideal of a set of points $X = \{\mathbf{x}_1, \ldots, \mathbf{x}_m\}\subseteq [0,1]^n$ is the set of polynomials that approximately evaluate to $0$ over all points $\mathbf{x} \in X$ and admits an efficient representation by a finite set of polynomials called generators. Algorithms that construct this set of generators are extensively studied but ultimately find little practical application because their computational complexities are thought to be superlinear in the number of samples $m$. In this paper, we focus on scaling up the Oracle Approximate Vanishing Ideal algorithm (OAVI), one of the most powerful of these methods. We prove that the computational complexity of OAVI is not superlinear but linear in the number of samples $m$ and polynomial in the number of features $n$, making OAVI an attractive preprocessing technique for large-scale machine learning. To further accelerate OAVI's training time, we propose two changes: First, as the name suggests, OAVI makes repeated oracle calls to convex solvers throughout its execution. By replacing the Pairwise Conditional Gradients algorithm, one of the standard solvers used in OAVI, with the faster Blended Pairwise Conditional Gradients algorithm, we illustrate how OAVI directly benefits from advancements in the study of convex solvers. Second, we propose Inverse Hessian Boosting (IHB): IHB exploits the fact that OAVI repeatedly solves quadratic convex optimization problems that differ only by very little and whose solutions can be written in closed form using inverse Hessian information. By efficiently updating the inverse of the Hessian matrix, the convex optimization problems can be solved almost instantly, accelerating OAVI's training time by up to multiple orders of magnitude. We complement our theoretical analysis with extensive numerical experiments on data sets whose sample numbers are in the millions.

Efficient Online-Bandit Strategies for Minimax Learning Problems

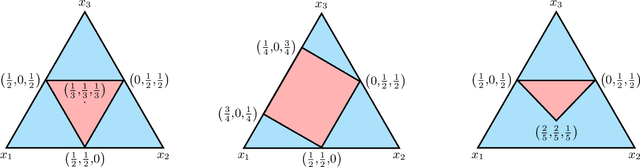
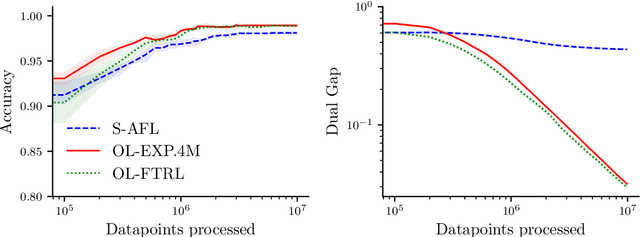
Several learning problems involve solving min-max problems, e.g., empirical distributional robust learning or learning with non-standard aggregated losses. More specifically, these problems are convex-linear problems where the minimization is carried out over the model parameters $w\in\mathcal{W}$ and the maximization over the empirical distribution $p\in\mathcal{K}$ of the training set indexes, where $\mathcal{K}$ is the simplex or a subset of it. To design efficient methods, we let an online learning algorithm play against a (combinatorial) bandit algorithm. We argue that the efficiency of such approaches critically depends on the structure of $\mathcal{K}$ and propose two properties of $\mathcal{K}$ that facilitate designing efficient algorithms. We focus on a specific family of sets $\mathcal{S}_{n,k}$ encompassing various learning applications and provide high-probability convergence guarantees to the minimax values.