SparseSwaps: Tractable LLM Pruning Mask Refinement at Scale

The resource requirements of Neural Networks can be significantly reduced through pruning -- the removal of seemingly less important parameters. However, with the rise of Large Language Models (LLMs), full retraining to recover pruning-induced performance degradation is often prohibitive and classical approaches such as global magnitude pruning are suboptimal on Transformer architectures. State-of-the-art methods hence solve a layer-wise mask selection problem, the problem of finding a pruning mask which minimizes the per-layer pruning error on a small set of calibration data. Exactly solving this problem to optimality using Integer Programming (IP) solvers is computationally infeasible due to its combinatorial nature and the size of the search space, and existing approaches therefore rely on approximations or heuristics. In this work, we demonstrate that the mask selection problem can be made drastically more tractable at LLM scale. To that end, we decouple the rows by enforcing equal sparsity levels per row. This allows us to derive optimal 1-swaps (exchanging one kept and one pruned weight) that can be computed efficiently using the Gram matrix of the calibration data. Using these observations, we propose a tractable and simple 1-swap algorithm that warm starts from any pruning mask, runs efficiently on GPUs at LLM scale, and is essentially hyperparameter-free. We demonstrate that our approach reduces per-layer pruning error by up to 60% over Wanda (Sun et al., 2023) and consistently improves perplexity and zero-shot accuracy across state-of-the-art GPT architectures.

Convex integer optimization with Frank-Wolfe methods

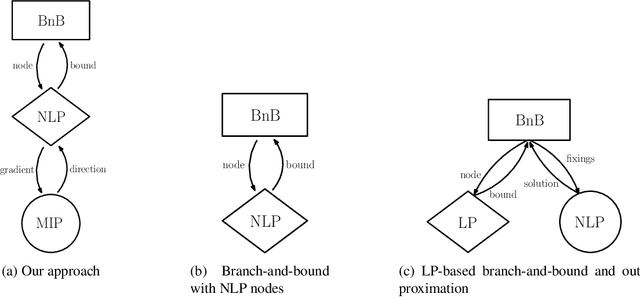
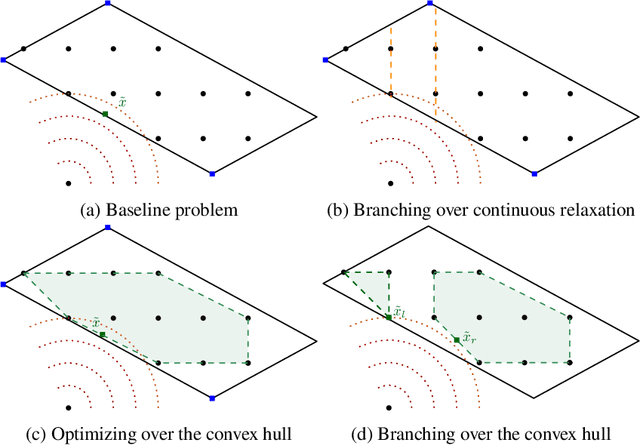
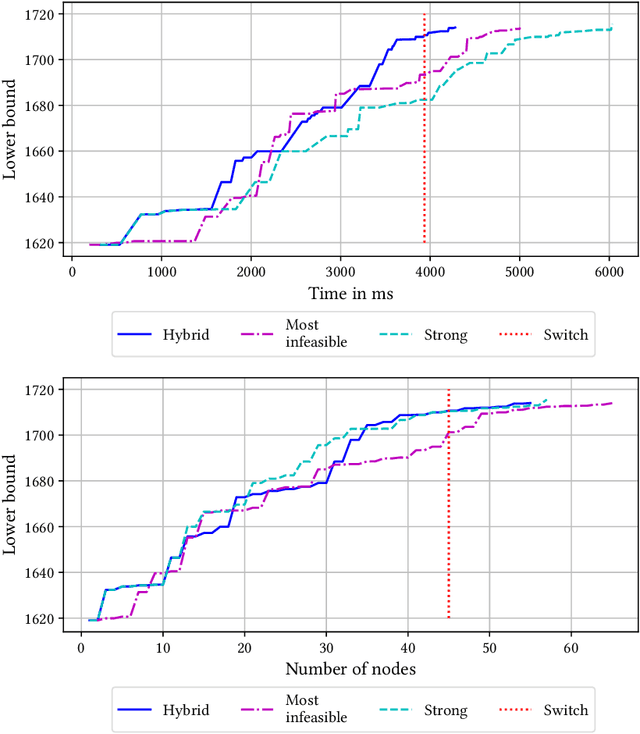
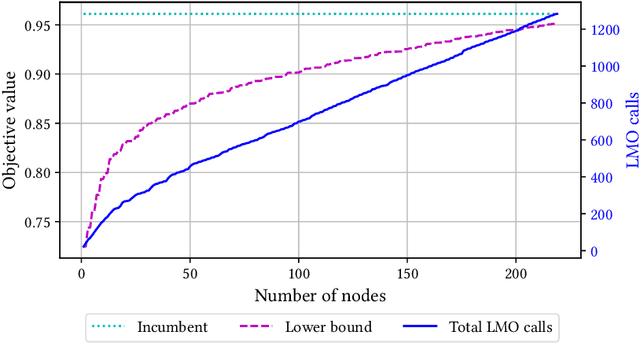
Mixed-integer nonlinear optimization is a broad class of problems that feature combinatorial structures and nonlinearities. Typical exact methods combine a branch-and-bound scheme with relaxation and separation subroutines. We investigate the properties and advantages of error-adaptive first-order methods based on the Frank-Wolfe algorithm for this setting, requiring only a gradient oracle for the objective function and linear optimization over the feasible set. In particular, we will study the algorithmic consequences of optimizing with a branch-and-bound approach where the subproblem is solved over the convex hull of the mixed-integer feasible set thanks to linear oracle calls, compared to solving the subproblems over the continuous relaxation of the same set. This novel approach computes feasible solutions while working on a single representation of the polyhedral constraints, leveraging the full extent of Mixed-Integer Programming (MIP) solvers without an outer approximation scheme.