Efficient Online-Bandit Strategies for Minimax Learning Problems
Paper and Code
Jun 04, 2021
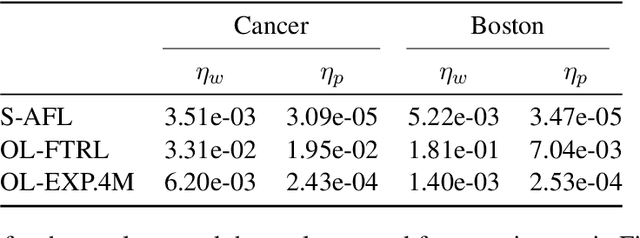
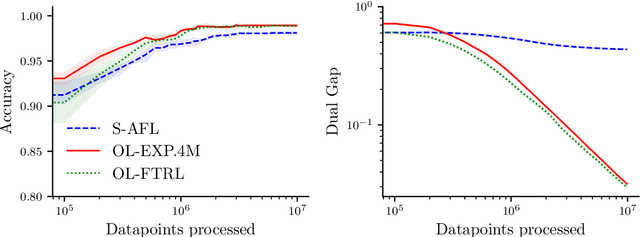

Several learning problems involve solving min-max problems, e.g., empirical distributional robust learning or learning with non-standard aggregated losses. More specifically, these problems are convex-linear problems where the minimization is carried out over the model parameters $w\in\mathcal{W}$ and the maximization over the empirical distribution $p\in\mathcal{K}$ of the training set indexes, where $\mathcal{K}$ is the simplex or a subset of it. To design efficient methods, we let an online learning algorithm play against a (combinatorial) bandit algorithm. We argue that the efficiency of such approaches critically depends on the structure of $\mathcal{K}$ and propose two properties of $\mathcal{K}$ that facilitate designing efficient algorithms. We focus on a specific family of sets $\mathcal{S}_{n,k}$ encompassing various learning applications and provide high-probability convergence guarantees to the minimax values.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge