A Free Lunch in LLM Compression: Revisiting Retraining after Pruning

While Neural Network pruning typically requires retraining the model to recover pruning-induced performance degradation, state-of-the-art Large Language Models (LLMs) pruning methods instead solve a layer-wise mask selection and reconstruction problem on a small set of calibration data to avoid full retraining, as it is considered computationally infeasible for LLMs. Reconstructing single matrices in isolation has favorable properties, such as convexity of the objective and significantly reduced memory requirements compared to full retraining. In practice, however, reconstruction is often implemented at coarser granularities, e.g., reconstructing a whole transformer block against its dense activations instead of a single matrix. In this work, we study the key design choices when reconstructing or retraining the remaining weights after pruning. We conduct an extensive computational study on state-of-the-art GPT architectures, and report several surprising findings that challenge common intuitions about retraining after pruning. In particular, we observe a free lunch scenario: reconstructing attention and MLP components separately within each transformer block is nearly the most resource-efficient yet achieves the best perplexity. Most importantly, this Pareto-optimal setup achieves better performance than full retraining, despite requiring only a fraction of the memory. Furthermore, we demonstrate that simple and efficient pruning criteria such as Wanda can outperform much more complex approaches when the reconstruction step is properly executed, highlighting its importance. Our findings challenge the narrative that retraining should be avoided at all costs and provide important insights into post-pruning performance recovery for LLMs.

S-CFE: Simple Counterfactual Explanations

We study the problem of finding optimal sparse, manifold-aligned counterfactual explanations for classifiers. Canonically, this can be formulated as an optimization problem with multiple non-convex components, including classifier loss functions and manifold alignment (or \emph{plausibility}) metrics. The added complexity of enforcing \emph{sparsity}, or shorter explanations, complicates the problem further. Existing methods often focus on specific models and plausibility measures, relying on convex $\ell_1$ regularizers to enforce sparsity. In this paper, we tackle the canonical formulation using the accelerated proximal gradient (APG) method, a simple yet efficient first-order procedure capable of handling smooth non-convex objectives and non-smooth $\ell_p$ (where $0 \leq p < 1$) regularizers. This enables our approach to seamlessly incorporate various classifiers and plausibility measures while producing sparser solutions. Our algorithm only requires differentiable data-manifold regularizers and supports box constraints for bounded feature ranges, ensuring the generated counterfactuals remain \emph{actionable}. Finally, experiments on real-world datasets demonstrate that our approach effectively produces sparse, manifold-aligned counterfactual explanations while maintaining proximity to the factual data and computational efficiency.

Group-wise Sparse and Explainable Adversarial Attacks

Sparse adversarial attacks fool deep neural networks (DNNs) through minimal pixel perturbations, typically regularized by the $\ell_0$ norm. Recent efforts have replaced this norm with a structural sparsity regularizer, such as the nuclear group norm, to craft group-wise sparse adversarial attacks. The resulting perturbations are thus explainable and hold significant practical relevance, shedding light on an even greater vulnerability of DNNs than previously anticipated. However, crafting such attacks poses an optimization challenge, as it involves computing norms for groups of pixels within a non-convex objective. In this paper, we tackle this challenge by presenting an algorithm that simultaneously generates group-wise sparse attacks within semantically meaningful areas of an image. In each iteration, the core operation of our algorithm involves the optimization of a quasinorm adversarial loss. This optimization is achieved by employing the $1/2$-quasinorm proximal operator for some iterations, a method tailored for nonconvex programming. Subsequently, the algorithm transitions to a projected Nesterov's accelerated gradient descent with $2$-norm regularization applied to perturbation magnitudes. We rigorously evaluate the efficacy of our novel attack in both targeted and non-targeted attack scenarios, on CIFAR-10 and ImageNet datasets. When compared to state-of-the-art methods, our attack consistently results in a remarkable increase in group-wise sparsity, e.g., an increase of $48.12\%$ on CIFAR-10 and $40.78\%$ on ImageNet (average case, targeted attack), all while maintaining lower perturbation magnitudes. Notably, this performance is complemented by a significantly faster computation time and a $100\%$ attack success rate.

Deep Semi-Supervised Learning for Time Series Classification

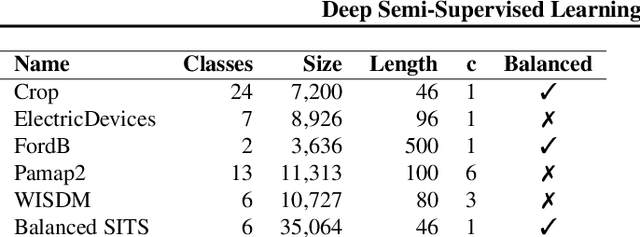
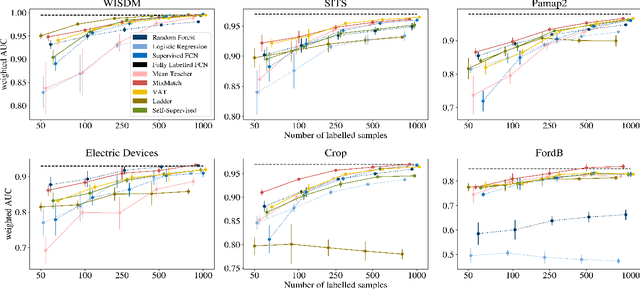
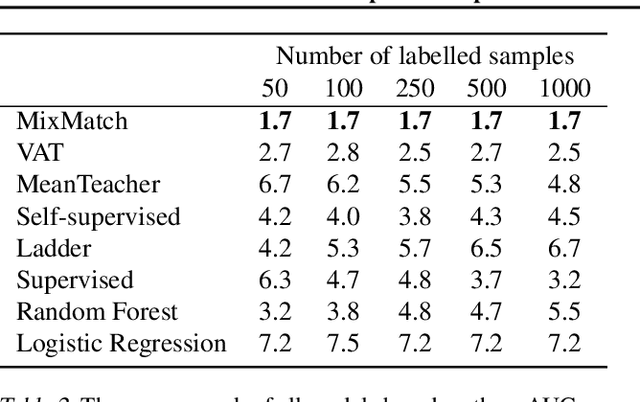
While Semi-supervised learning has gained much attention in computer vision on image data, yet limited research exists on its applicability in the time series domain. In this work, we investigate the transferability of state-of-the-art deep semi-supervised models from image to time series classification. We discuss the necessary model adaptations, in particular an appropriate model backbone architecture and the use of tailored data augmentation strategies. Based on these adaptations, we explore the potential of deep semi-supervised learning in the context of time series classification by evaluating our methods on large public time series classification problems with varying amounts of labelled samples. We perform extensive comparisons under a decidedly realistic and appropriate evaluation scheme with a unified reimplementation of all algorithms considered, which is yet lacking in the field. We find that these transferred semi-supervised models show significant performance gains over strong supervised, semi-supervised and self-supervised alternatives, especially for scenarios with very few labelled samples.