Carlos Guestrin
Carnegie Mellon University
VTA: An Open Hardware-Software Stack for Deep Learning
Jul 11, 2018
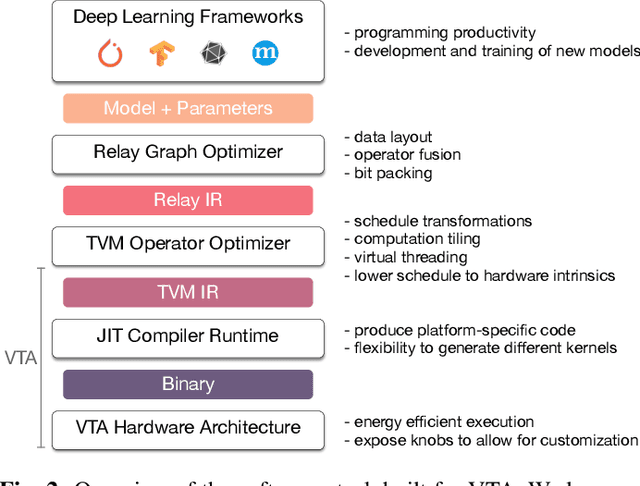
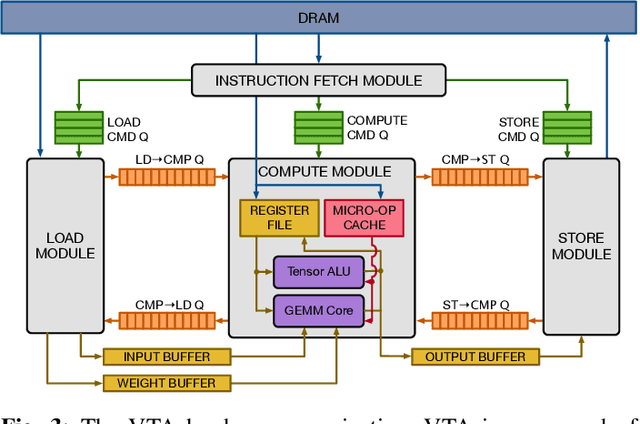
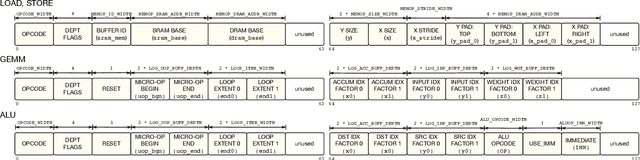
Abstract:Hardware acceleration is an enabler for ubiquitous and efficient deep learning. With hardware accelerators being introduced in datacenter and edge devices, it is time to acknowledge that hardware specialization is central to the deep learning system stack. This technical report presents the Versatile Tensor Accelerator (VTA), an open, generic, and customizable deep learning accelerator design. VTA is a programmable accelerator that exposes a RISC-like programming abstraction to describe operations at the tensor level. We designed VTA to expose the most salient and common characteristics of mainstream deep learning accelerators, such as tensor operations, DMA load/stores, and explicit compute/memory arbitration. VTA is more than a standalone accelerator design: it's an end-to-end solution that includes drivers, a JIT runtime, and an optimizing compiler stack based on TVM. The current release of VTA includes a behavioral hardware simulator, as well as the infrastructure to deploy VTA on low-cost FPGA development boards for fast prototyping. By extending the TVM stack with a customizable, and open source deep learning hardware accelerator design, we are exposing a transparent end-to-end deep learning stack from the high-level deep learning framework, down to the actual hardware design and implementation. This forms a truly end-to-end, from software-to-hardware open source stack for deep learning systems.
Compact Factorization of Matrices Using Generalized Round-Rank
May 01, 2018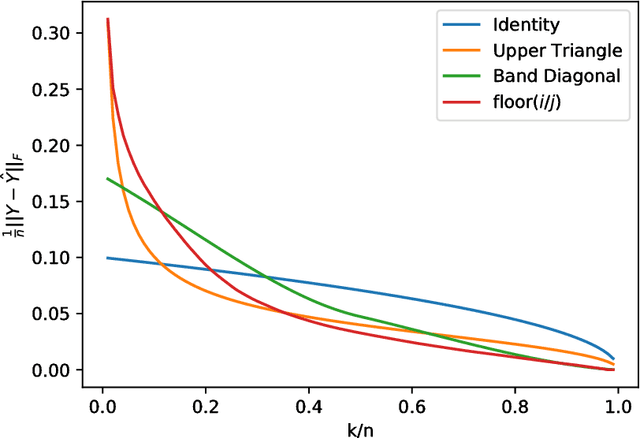
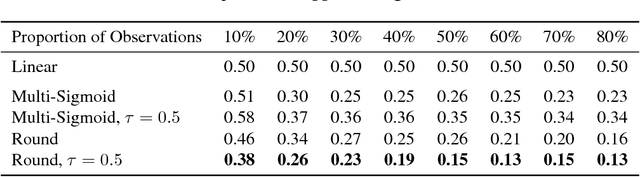
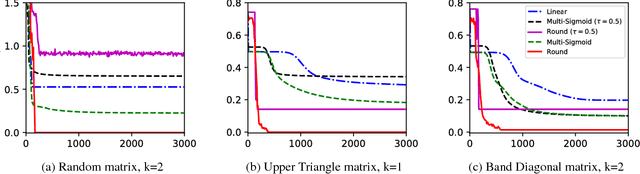
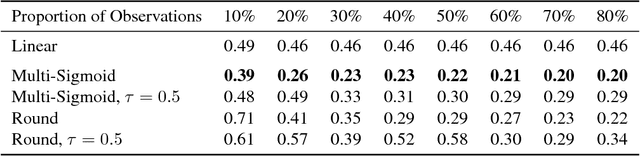
Abstract:Matrix factorization is a well-studied task in machine learning for compactly representing large, noisy data. In our approach, instead of using the traditional concept of matrix rank, we define a new notion of link-rank based on a non-linear link function used within factorization. In particular, by applying the round function on a factorization to obtain ordinal-valued matrices, we introduce generalized round-rank (GRR). We show that not only are there many full-rank matrices that are low GRR, but further, that these matrices cannot be approximated well by low-rank linear factorization. We provide uniqueness conditions of this formulation and provide gradient descent-based algorithms. Finally, we present experiments on real-world datasets to demonstrate that the GRR-based factorization is significantly more accurate than linear factorization, while converging faster and using lower rank representations.
Programs as Black-Box Explanations
Nov 22, 2016
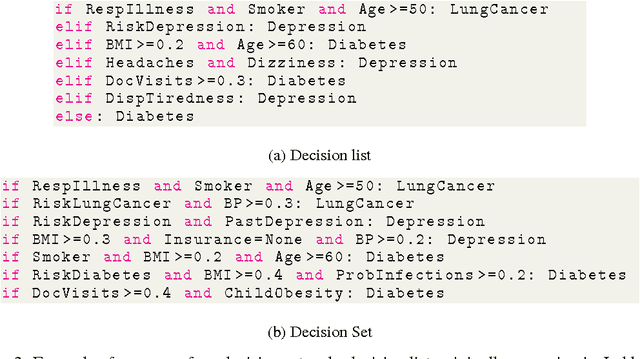
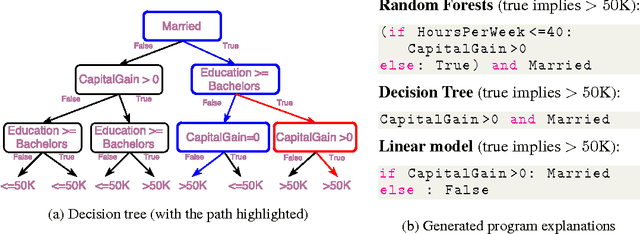
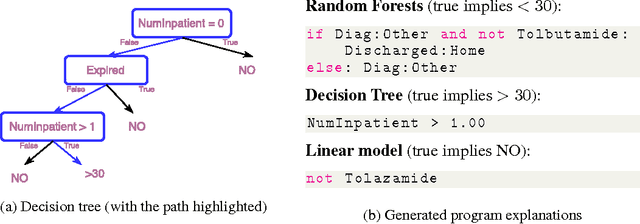
Abstract:Recent work in model-agnostic explanations of black-box machine learning has demonstrated that interpretability of complex models does not have to come at the cost of accuracy or model flexibility. However, it is not clear what kind of explanations, such as linear models, decision trees, and rule lists, are the appropriate family to consider, and different tasks and models may benefit from different kinds of explanations. Instead of picking a single family of representations, in this work we propose to use "programs" as model-agnostic explanations. We show that small programs can be expressive yet intuitive as explanations, and generalize over a number of existing interpretable families. We propose a prototype program induction method based on simulated annealing that approximates the local behavior of black-box classifiers around a specific prediction using random perturbations. Finally, we present preliminary application on small datasets and show that the generated explanations are intuitive and accurate for a number of classifiers.
Nothing Else Matters: Model-Agnostic Explanations By Identifying Prediction Invariance
Nov 17, 2016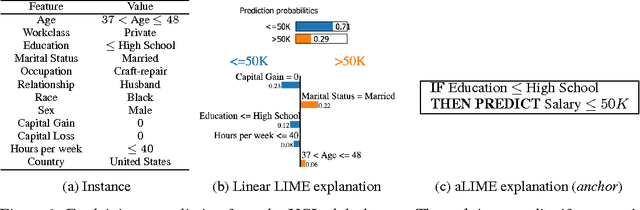

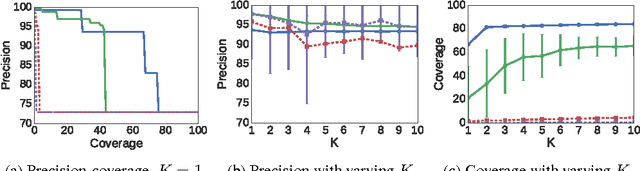

Abstract:At the core of interpretable machine learning is the question of whether humans are able to make accurate predictions about a model's behavior. Assumed in this question are three properties of the interpretable output: coverage, precision, and effort. Coverage refers to how often humans think they can predict the model's behavior, precision to how accurate humans are in those predictions, and effort is either the up-front effort required in interpreting the model, or the effort required to make predictions about a model's behavior. In this work, we propose anchor-LIME (aLIME), a model-agnostic technique that produces high-precision rule-based explanations for which the coverage boundaries are very clear. We compare aLIME to linear LIME with simulated experiments, and demonstrate the flexibility of aLIME with qualitative examples from a variety of domains and tasks.
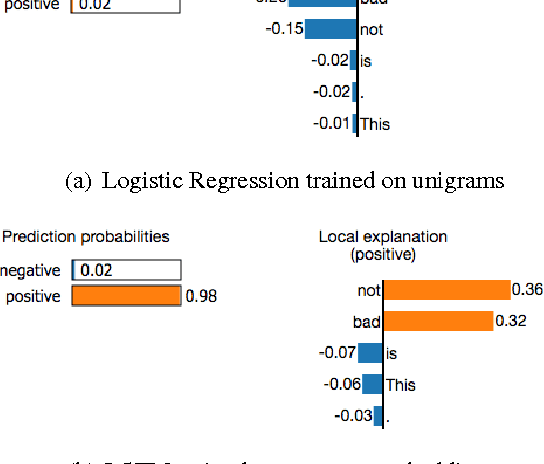
"Why Should I Trust You?": Explaining the Predictions of Any Classifier
Aug 09, 2016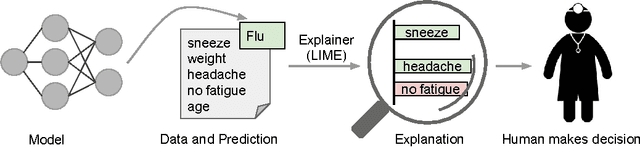
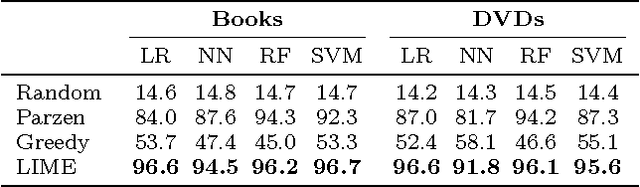


Abstract:Despite widespread adoption, machine learning models remain mostly black boxes. Understanding the reasons behind predictions is, however, quite important in assessing trust, which is fundamental if one plans to take action based on a prediction, or when choosing whether to deploy a new model. Such understanding also provides insights into the model, which can be used to transform an untrustworthy model or prediction into a trustworthy one. In this work, we propose LIME, a novel explanation technique that explains the predictions of any classifier in an interpretable and faithful manner, by learning an interpretable model locally around the prediction. We also propose a method to explain models by presenting representative individual predictions and their explanations in a non-redundant way, framing the task as a submodular optimization problem. We demonstrate the flexibility of these methods by explaining different models for text (e.g. random forests) and image classification (e.g. neural networks). We show the utility of explanations via novel experiments, both simulated and with human subjects, on various scenarios that require trust: deciding if one should trust a prediction, choosing between models, improving an untrustworthy classifier, and identifying why a classifier should not be trusted.
Model-Agnostic Interpretability of Machine Learning
Jun 16, 2016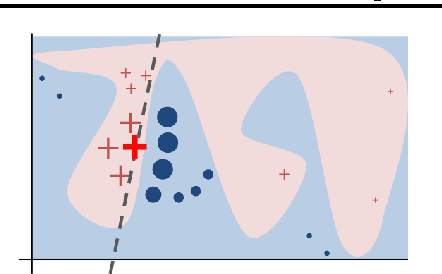
Abstract:Understanding why machine learning models behave the way they do empowers both system designers and end-users in many ways: in model selection, feature engineering, in order to trust and act upon the predictions, and in more intuitive user interfaces. Thus, interpretability has become a vital concern in machine learning, and work in the area of interpretable models has found renewed interest. In some applications, such models are as accurate as non-interpretable ones, and thus are preferred for their transparency. Even when they are not accurate, they may still be preferred when interpretability is of paramount importance. However, restricting machine learning to interpretable models is often a severe limitation. In this paper we argue for explaining machine learning predictions using model-agnostic approaches. By treating the machine learning models as black-box functions, these approaches provide crucial flexibility in the choice of models, explanations, and representations, improving debugging, comparison, and interfaces for a variety of users and models. We also outline the main challenges for such methods, and review a recently-introduced model-agnostic explanation approach (LIME) that addresses these challenges.
XGBoost: A Scalable Tree Boosting System
Jun 10, 2016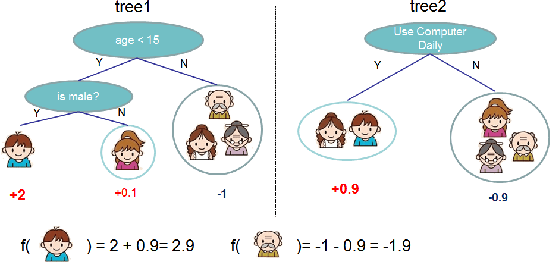

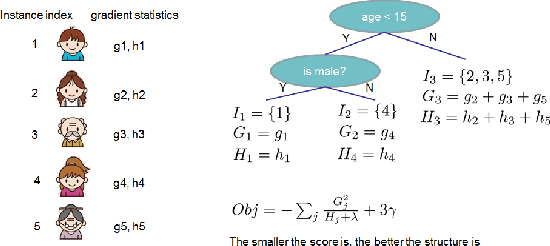
Abstract:Tree boosting is a highly effective and widely used machine learning method. In this paper, we describe a scalable end-to-end tree boosting system called XGBoost, which is used widely by data scientists to achieve state-of-the-art results on many machine learning challenges. We propose a novel sparsity-aware algorithm for sparse data and weighted quantile sketch for approximate tree learning. More importantly, we provide insights on cache access patterns, data compression and sharding to build a scalable tree boosting system. By combining these insights, XGBoost scales beyond billions of examples using far fewer resources than existing systems.
Scaling Submodular Maximization via Pruned Submodularity Graphs
Jun 01, 2016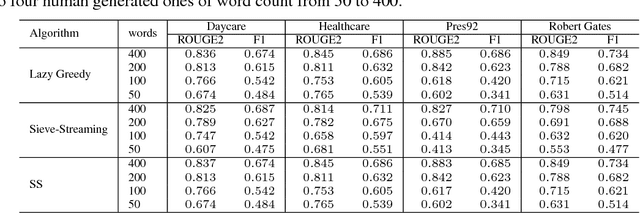
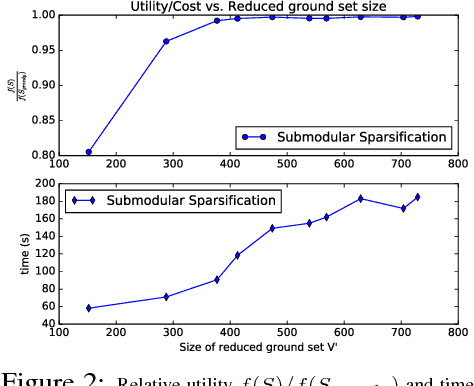
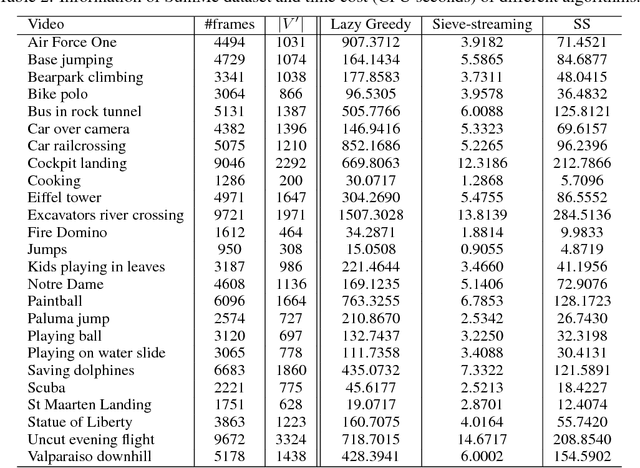
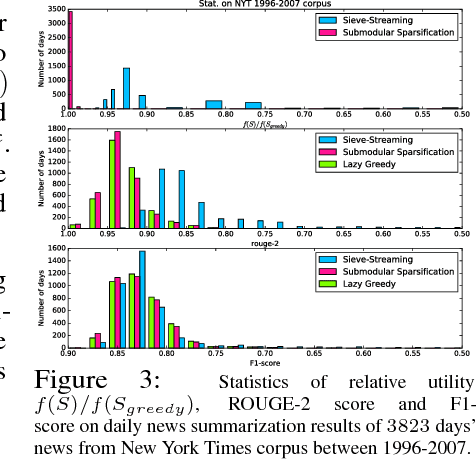
Abstract:We propose a new random pruning method (called "submodular sparsification (SS)") to reduce the cost of submodular maximization. The pruning is applied via a "submodularity graph" over the $n$ ground elements, where each directed edge is associated with a pairwise dependency defined by the submodular function. In each step, SS prunes a $1-1/\sqrt{c}$ (for $c>1$) fraction of the nodes using weights on edges computed based on only a small number ($O(\log n)$) of randomly sampled nodes. The algorithm requires $\log_{\sqrt{c}}n$ steps with a small and highly parallelizable per-step computation. An accuracy-speed tradeoff parameter $c$, set as $c = 8$, leads to a fast shrink rate $\sqrt{2}/4$ and small iteration complexity $\log_{2\sqrt{2}}n$. Analysis shows that w.h.p., the greedy algorithm on the pruned set of size $O(\log^2 n)$ can achieve a guarantee similar to that of processing the original dataset. In news and video summarization tasks, SS is able to substantially reduce both computational costs and memory usage, while maintaining (or even slightly exceeding) the quality of the original (and much more costly) greedy algorithm.
Training Deep Nets with Sublinear Memory Cost
Apr 22, 2016
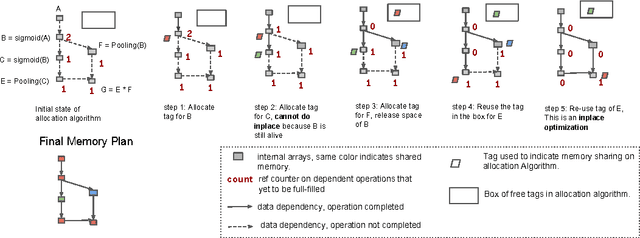
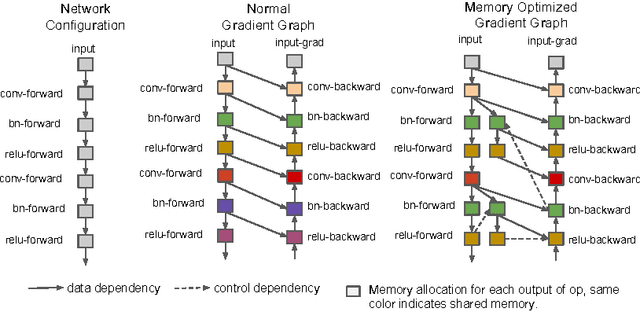
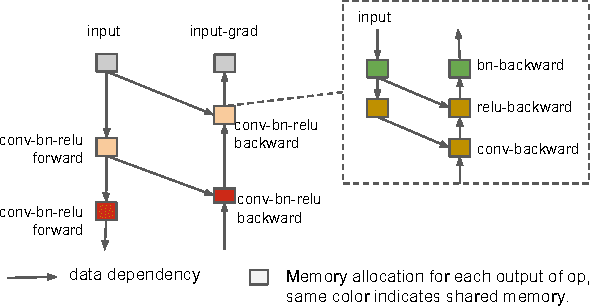
Abstract:We propose a systematic approach to reduce the memory consumption of deep neural network training. Specifically, we design an algorithm that costs O(sqrt(n)) memory to train a n layer network, with only the computational cost of an extra forward pass per mini-batch. As many of the state-of-the-art models hit the upper bound of the GPU memory, our algorithm allows deeper and more complex models to be explored, and helps advance the innovations in deep learning research. We focus on reducing the memory cost to store the intermediate feature maps and gradients during training. Computation graph analysis is used for automatic in-place operation and memory sharing optimizations. We show that it is possible to trade computation for memory - giving a more memory efficient training algorithm with a little extra computation cost. In the extreme case, our analysis also shows that the memory consumption can be reduced to O(log n) with as little as O(n log n) extra cost for forward computation. Our experiments show that we can reduce the memory cost of a 1,000-layer deep residual network from 48G to 7G with only 30 percent additional running time cost on ImageNet problems. Similarly, significant memory cost reduction is observed in training complex recurrent neural networks on very long sequences.
Divide-and-Conquer Learning by Anchoring a Conical Hull
Jun 22, 2014

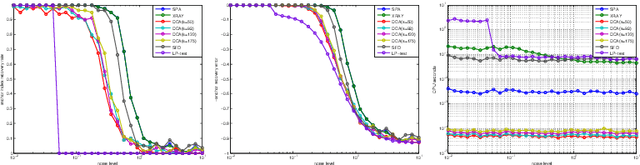
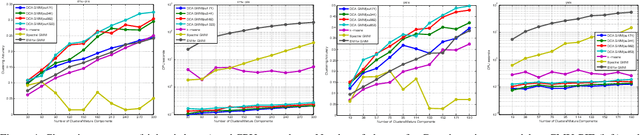
Abstract:We reduce a broad class of machine learning problems, usually addressed by EM or sampling, to the problem of finding the $k$ extremal rays spanning the conical hull of a data point set. These $k$ "anchors" lead to a global solution and a more interpretable model that can even outperform EM and sampling on generalization error. To find the $k$ anchors, we propose a novel divide-and-conquer learning scheme "DCA" that distributes the problem to $\mathcal O(k\log k)$ same-type sub-problems on different low-D random hyperplanes, each can be solved by any solver. For the 2D sub-problem, we present a non-iterative solver that only needs to compute an array of cosine values and its max/min entries. DCA also provides a faster subroutine for other methods to check whether a point is covered in a conical hull, which improves algorithm design in multiple dimensions and brings significant speedup to learning. We apply our method to GMM, HMM, LDA, NMF and subspace clustering, then show its competitive performance and scalability over other methods on rich datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge