Structured Prediction with Abstention via the Lovász Hinge

The Lov\'asz hinge is a convex loss function proposed for binary structured classification, in which k related binary predictions jointly evaluated by a submodular function. Despite its prevalence in image segmentation and related tasks, the consistency of the Lov\'asz hinge has remained open. We show that the Lov\'asz hinge is inconsistent with its desired target unless the set function used for evaluation is modular. Leveraging the embedding framework of Finocchiaro et al. (2024), we find the target loss for which the Lov\'asz hinge is consistent. This target, which we call the structured abstain problem, is a variant of selective classification for structured prediction that allows one to abstain on any subset of the k binary predictions. We derive a family of link functions, each of which is simultaneously consistent for all polymatroids, a subset of submodular set functions. We then give sufficient conditions on the polymatroid for the structured abstain problem to be tightly embedded by the Lov\'asz hinge, meaning no target prediction is redundant. We experimentally demonstrate the potential of the structured abstain problem for interpretability in structured classification tasks. Finally, for the multiclass setting, we show that one can combine the binary encoding construction of Ramaswamy et al. (2018) with our link construction to achieve an efficient consistent surrogate for a natural multiclass generalization of the structured abstain problem.

Smooth Quadratic Prediction Markets

When agents trade in a Duality-based Cost Function prediction market, they collectively implement the learning algorithm Follow-The-Regularized-Leader. We ask whether other learning algorithms could be used to inspire the design of prediction markets. By decomposing and modifying the Duality-based Cost Function Market Maker's (DCFMM) pricing mechanism, we propose a new prediction market, called the Smooth Quadratic Prediction Market, the incentivizes agents to collectively implement general steepest gradient descent. Relative to the DCFMM, the Smooth Quadratic Prediction Market has a better worst-case monetary loss for AD securities while preserving axiom guarantees such as the existence of instantaneous price, information incorporation, expressiveness, no arbitrage, and a form of incentive compatibility. To motivate the application of the Smooth Quadratic Prediction Market, we independently examine agents' trading behavior under two realistic constraints: bounded budgets and buy-only securities. Finally, we provide an introductory analysis of an approach to facilitate adaptive liquidity using the Smooth Quadratic Prediction Market. Our results suggest future designs where the price update rule is separate from the fee structure, yet guarantees are preserved.

Trading off Consistency and Dimensionality of Convex Surrogates for the Mode

In multiclass classification over $n$ outcomes, the outcomes must be embedded into the reals with dimension at least $n-1$ in order to design a consistent surrogate loss that leads to the "correct" classification, regardless of the data distribution. For large $n$, such as in information retrieval and structured prediction tasks, optimizing a surrogate in $n-1$ dimensions is often intractable. We investigate ways to trade off surrogate loss dimension, the number of problem instances, and restricting the region of consistency in the simplex for multiclass classification. Following past work, we examine an intuitive embedding procedure that maps outcomes into the vertices of convex polytopes in a low-dimensional surrogate space. We show that full-dimensional subsets of the simplex exist around each point mass distribution for which consistency holds, but also, with less than $n-1$ dimensions, there exist distributions for which a phenomenon called hallucination occurs, which is when the optimal report under the surrogate loss is an outcome with zero probability. Looking towards application, we derive a result to check if consistency holds under a given polytope embedding and low-noise assumption, providing insight into when to use a particular embedding. We provide examples of embedding $n = 2^{d}$ outcomes into the $d$-dimensional unit cube and $n = d!$ outcomes into the $d$-dimensional permutahedron under low-noise assumptions. Finally, we demonstrate that with multiple problem instances, we can learn the mode with $\frac{n}{2}$ dimensions over the whole simplex.

The Structured Abstain Problem and the Lovász Hinge

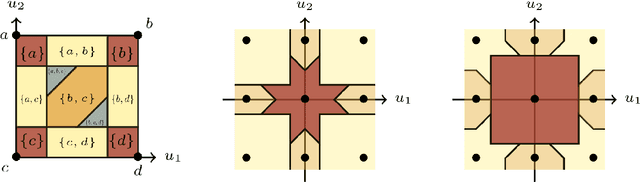
The Lov\'asz hinge is a convex surrogate recently proposed for structured binary classification, in which $k$ binary predictions are made simultaneously and the error is judged by a submodular set function. Despite its wide usage in image segmentation and related problems, its consistency has remained open. We resolve this open question, showing that the Lov\'asz hinge is inconsistent for its desired target unless the set function is modular. Leveraging a recent embedding framework, we instead derive the target loss for which the Lov\'asz hinge is consistent. This target, which we call the structured abstain problem, allows one to abstain on any subset of the $k$ predictions. We derive two link functions, each of which are consistent for all submodular set functions simultaneously.