Multi-Agent Path Finding For Large Agents Is Intractable

The multi-agent path finding (MAPF) problem asks to find a set of paths on a graph such that when synchronously following these paths the agents never encounter a conflict. In the most widespread MAPF formulation, the so-called Classical MAPF, the agents sizes are neglected and two types of conflicts are considered: occupying the same vertex or using the same edge at the same time step. Meanwhile in numerous practical applications, e.g. in robotics, taking into account the agents' sizes is vital to ensure that the MAPF solutions can be safely executed. Introducing large agents yields an additional type of conflict arising when one agent follows an edge and its body overlaps with the body of another agent that is actually not using this same edge (e.g. staying still at some distinct vertex of the graph). Until now it was not clear how harder the problem gets when such conflicts are to be considered while planning. Specifically, it was known that Classical MAPF problem on an undirected graph can be solved in polynomial time, however no complete polynomial-time algorithm was presented to solve MAPF with large agents. In this paper we, for the first time, establish that the latter problem is NP-hard and, thus, if P!=NP no polynomial algorithm for it can, unfortunately, be presented. Our proof is based on the prevalent in the field technique of reducing the seminal 3SAT problem (which is known to be an NP-complete problem) to the problem at hand. In particular, for an arbitrary 3SAT formula we procedurally construct a dedicated graph with specific start and goal vertices and show that the given 3SAT formula is satisfiable iff the corresponding path finding instance has a solution.

In Quest of Ground Truth: Learning Confident Models and Estimating Uncertainty in the Presence of Annotator Noise

The performance of the Deep Learning (DL) models depends on the quality of labels. In some areas, the involvement of human annotators may lead to noise in the data. When these corrupted labels are blindly regarded as the ground truth (GT), DL models suffer from performance deficiency. This paper presents a method that aims to learn a confident model in the presence of noisy labels. This is done in conjunction with estimating the uncertainty of multiple annotators. We robustly estimate the predictions given only the noisy labels by adding entropy or information-based regularizer to the classifier network. We conduct our experiments on a noisy version of MNIST, CIFAR-10, and FMNIST datasets. Our empirical results demonstrate the robustness of our method as it outperforms or performs comparably to other state-of-the-art (SOTA) methods. In addition, we evaluated the proposed method on the curated dataset, where the noise type and level of various annotators depend on the input image style. We show that our approach performs well and is adept at learning annotators' confusion. Moreover, we demonstrate how our model is more confident in predicting GT than other baselines. Finally, we assess our approach for segmentation problem and showcase its effectiveness with experiments.

FLECS-CGD: A Federated Learning Second-Order Framework via Compression and Sketching with Compressed Gradient Differences

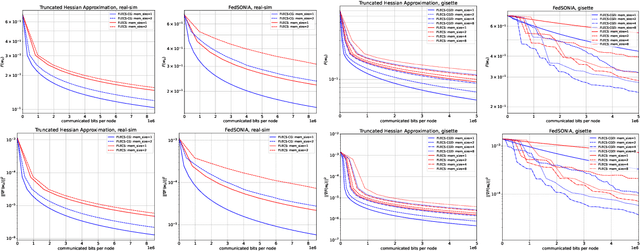
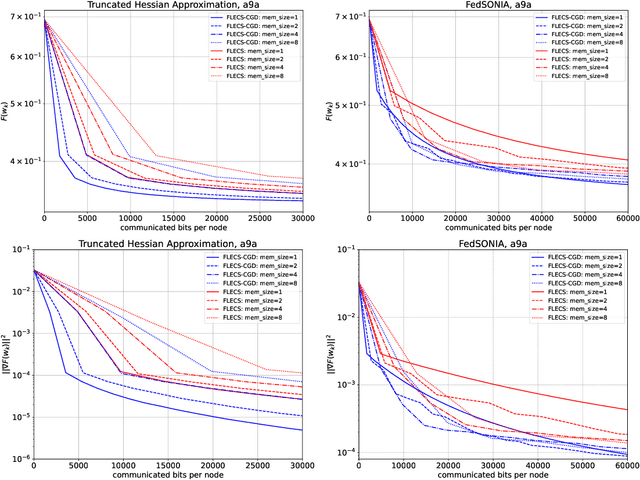
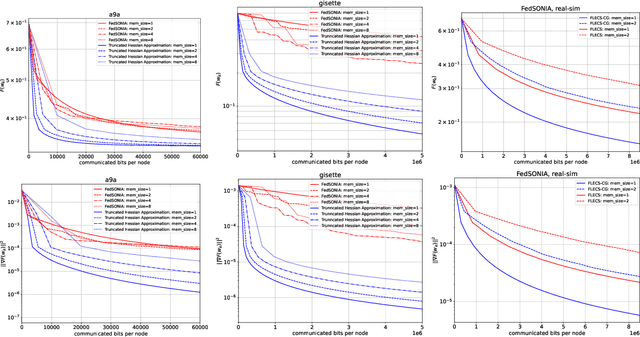
In the recent paper FLECS (Agafonov et al, FLECS: A Federated Learning Second-Order Framework via Compression and Sketching), the second-order framework FLECS was proposed for the Federated Learning problem. This method utilize compression of sketched Hessians to make communication costs low. However, the main bottleneck of FLECS is gradient communication without compression. In this paper, we propose the modification of FLECS with compressed gradient differences, which we call FLECS-CGD (FLECS with Compressed Gradient Differences) and make it applicable for stochastic optimization. Convergence guarantees are provided in strongly convex and nonconvex cases. Experiments show the practical benefit of proposed approach.