Unbiased Smoothing using Particle Independent Metropolis-Hastings

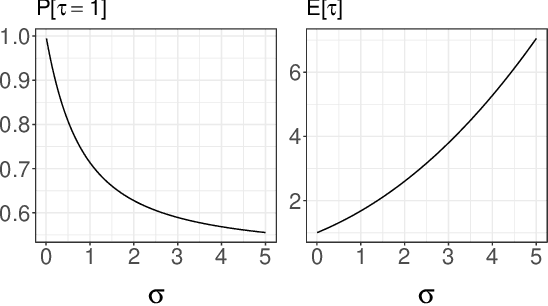
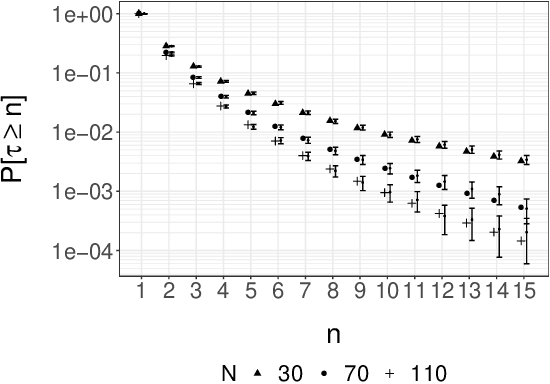
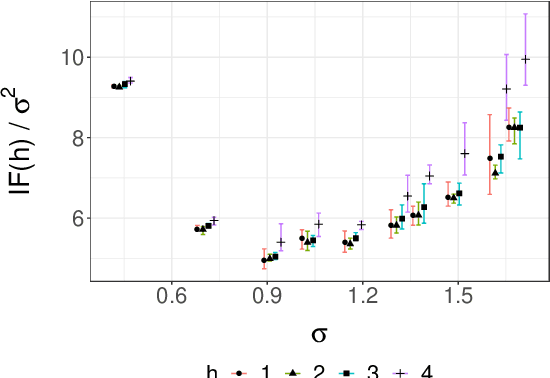
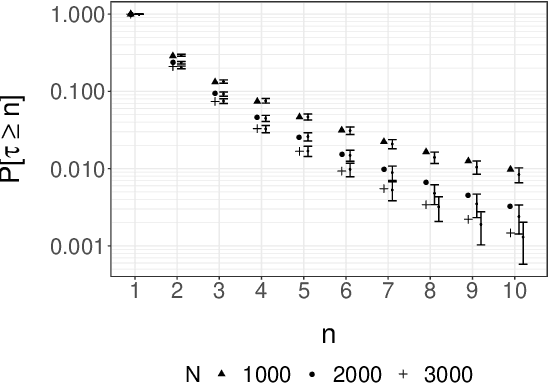
We consider the approximation of expectations with respect to the distribution of a latent Markov process given noisy measurements. This is known as the smoothing problem and is often approached with particle and Markov chain Monte Carlo (MCMC) methods. These methods provide consistent but biased estimators when run for a finite time. We propose a simple way of coupling two MCMC chains built using Particle Independent Metropolis-Hastings (PIMH) to produce unbiased smoothing estimators. Unbiased estimators are appealing in the context of parallel computing, and facilitate the construction of confidence intervals. The proposed scheme only requires access to off-the-shelf Particle Filters (PF) and is thus easier to implement than recently proposed unbiased smoothers. The approach is demonstrated on a L\'evy-driven stochastic volatility model and a stochastic kinetic model.

Scalable Metropolis-Hastings for Exact Bayesian Inference with Large Datasets

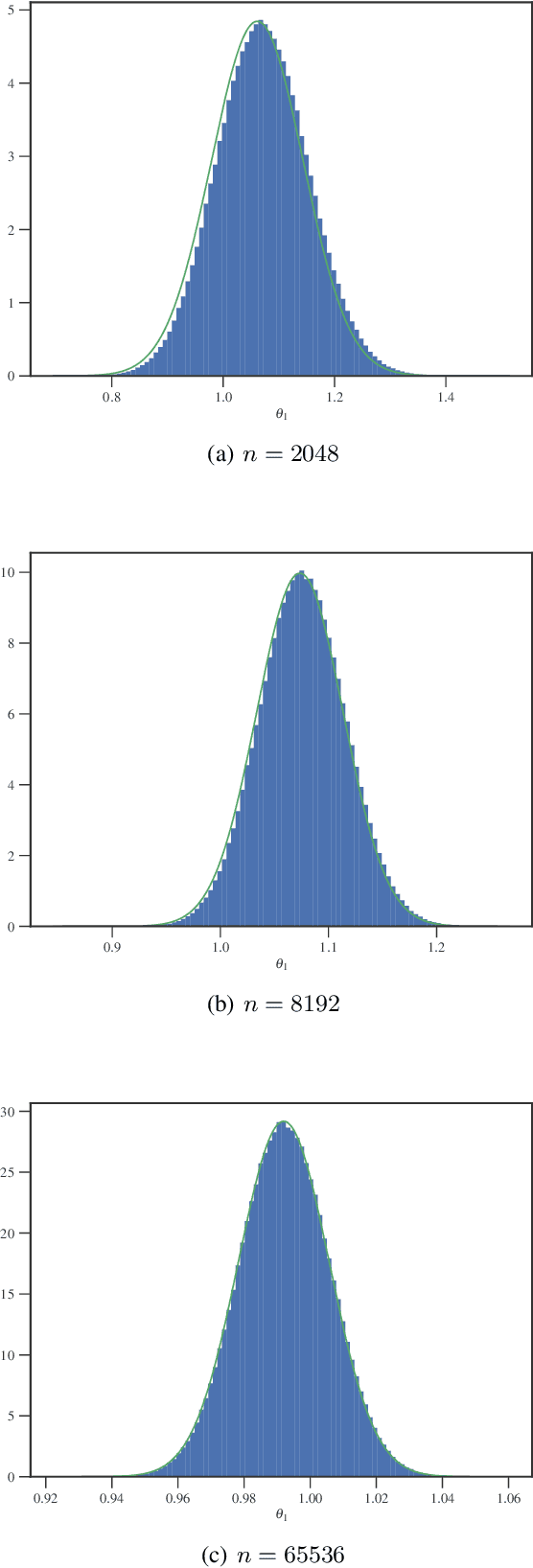
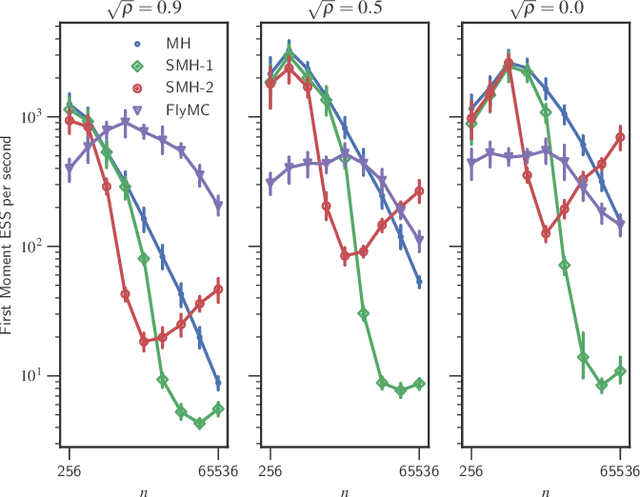
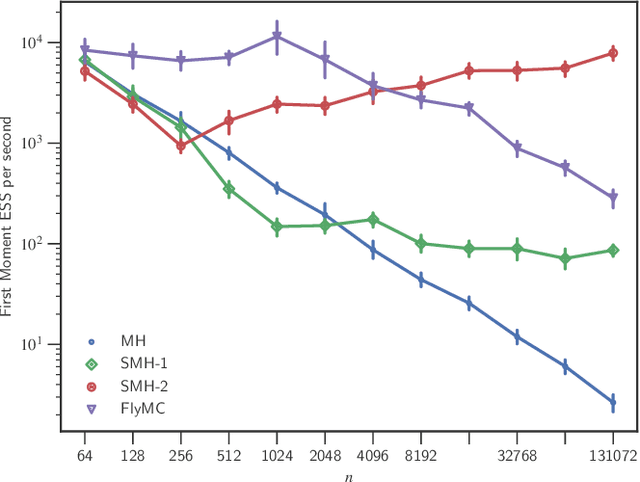
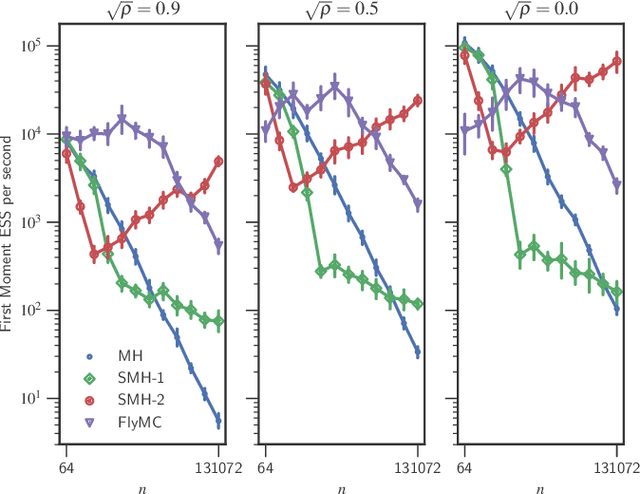
Bayesian inference via standard Markov Chain Monte Carlo (MCMC) methods such as Metropolis-Hastings is too computationally intensive to handle large datasets, since the cost per step usually scales like $O(n)$ in the number of data points $n$. We propose the Scalable Metropolis-Hastings (SMH) kernel that exploits Gaussian concentration of the posterior to require processing on average only $O(1)$ or even $O(1/\sqrt{n})$ data points per step. This scheme is based on a combination of factorized acceptance probabilities, procedures for fast simulation of Bernoulli processes, and control variate ideas. Contrary to many MCMC subsampling schemes such as fixed step-size Stochastic Gradient Langevin Dynamics, our approach is exact insofar as the invariant distribution is the true posterior and not an approximation to it. We characterise the performance of our algorithm theoretically, and give realistic and verifiable conditions under which it is geometrically ergodic. This theory is borne out by empirical results that demonstrate overall performance benefits over standard Metropolis-Hastings and various subsampling algorithms.

On the Selection of Initialization and Activation Function for Deep Neural Networks

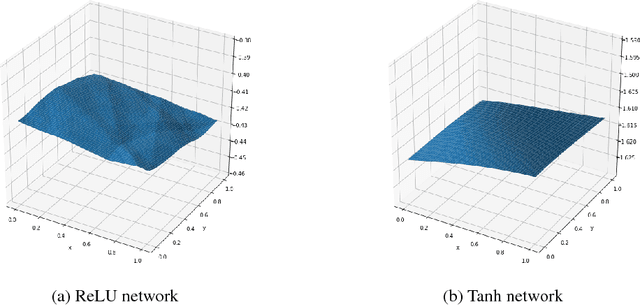
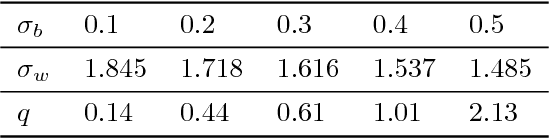
The weight initialization and the activation function of deep neural networks have a crucial impact on the performance of the training procedure. An inappropriate selection can lead to the loss of information of the input during forward propagation and the exponential vanishing/exploding of gradients during back-propagation. Understanding the theoretical properties of untrained random networks is key to identifying which deep networks may be trained successfully as recently demonstrated by Schoenholz et al. (2017) who showed that for deep feedforward neural networks only a specific choice of hyperparameters known as the `edge of chaos' can lead to good performance. We complete this analysis by providing quantitative results showing that, for a class of ReLU-like activation functions, the information propagates indeed deeper for an initialization at the edge of chaos. By further extending this analysis, we identify a class of activation functions that improve the information propagation over ReLU-like functions. This class includes the Swish activation, $\phi_{swish}(x) = x \cdot \text{sigmoid}(x)$, used in Hendrycks & Gimpel (2016), Elfwing et al. (2017) and Ramachandran et al. (2017). This provides a theoretical grounding for the excellent empirical performance of $\phi_{swish}$ observed in these contributions. We complement those previous results by illustrating the benefit of using a random initialization on the edge of chaos in this context.

Hamiltonian Descent Methods

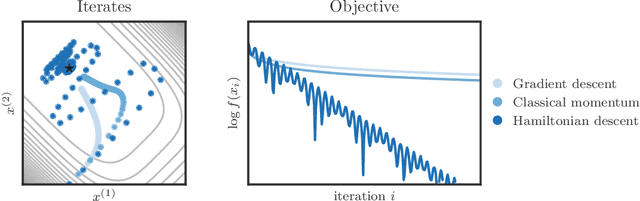
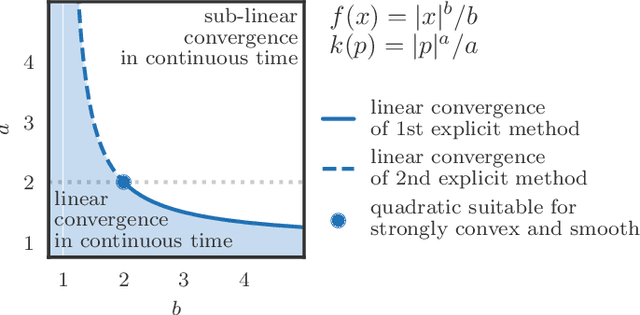
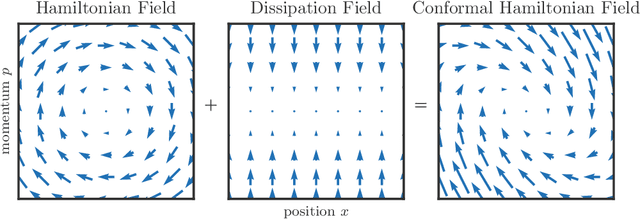
We propose a family of optimization methods that achieve linear convergence using first-order gradient information and constant step sizes on a class of convex functions much larger than the smooth and strongly convex ones. This larger class includes functions whose second derivatives may be singular or unbounded at their minima. Our methods are discretizations of conformal Hamiltonian dynamics, which generalize the classical momentum method to model the motion of a particle with non-standard kinetic energy exposed to a dissipative force and the gradient field of the function of interest. They are first-order in the sense that they require only gradient computation. Yet, crucially the kinetic gradient map can be designed to incorporate information about the convex conjugate in a fashion that allows for linear convergence on convex functions that may be non-smooth or non-strongly convex. We study in detail one implicit and two explicit methods. For one explicit method, we provide conditions under which it converges to stationary points of non-convex functions. For all, we provide conditions on the convex function and kinetic energy pair that guarantee linear convergence, and show that these conditions can be satisfied by functions with power growth. In sum, these methods expand the class of convex functions on which linear convergence is possible with first-order computation.

Asymptotic Properties of Recursive Maximum Likelihood Estimation in Non-Linear State-Space Models

Using stochastic gradient search and the optimal filter derivative, it is possible to perform recursive (i.e., online) maximum likelihood estimation in a non-linear state-space model. As the optimal filter and its derivative are analytically intractable for such a model, they need to be approximated numerically. In [Poyiadjis, Doucet and Singh, Biometrika 2018], a recursive maximum likelihood algorithm based on a particle approximation to the optimal filter derivative has been proposed and studied through numerical simulations. Here, this algorithm and its asymptotic behavior are analyzed theoretically. We show that the algorithm accurately estimates maxima to the underlying (average) log-likelihood when the number of particles is sufficiently large. We also derive (relatively) tight bounds on the estimation error. The obtained results hold under (relatively) mild conditions and cover several classes of non-linear state-space models met in practice.

Hamiltonian Variational Auto-Encoder

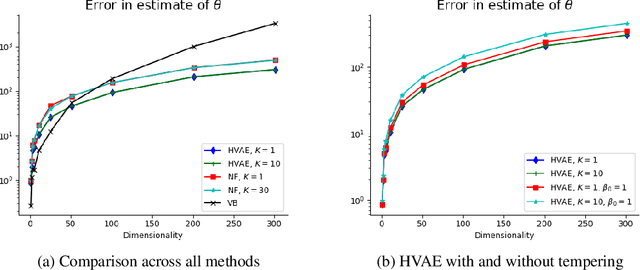
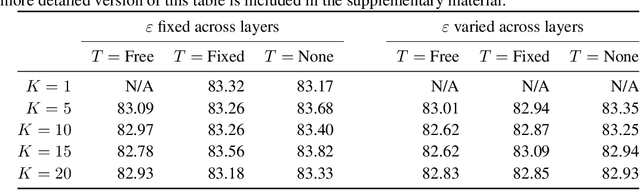
Variational Auto-Encoders (VAEs) have become very popular techniques to perform inference and learning in latent variable models as they allow us to leverage the rich representational power of neural networks to obtain flexible approximations of the posterior of latent variables as well as tight evidence lower bounds (ELBOs). Combined with stochastic variational inference, this provides a methodology scaling to large datasets. However, for this methodology to be practically efficient, it is necessary to obtain low-variance unbiased estimators of the ELBO and its gradients with respect to the parameters of interest. While the use of Markov chain Monte Carlo (MCMC) techniques such as Hamiltonian Monte Carlo (HMC) has been previously suggested to achieve this [23, 26], the proposed methods require specifying reverse kernels which have a large impact on performance. Additionally, the resulting unbiased estimator of the ELBO for most MCMC kernels is typically not amenable to the reparameterization trick. We show here how to optimally select reverse kernels in this setting and, by building upon Hamiltonian Importance Sampling (HIS) [17], we obtain a scheme that provides low-variance unbiased estimators of the ELBO and its gradients using the reparameterization trick. This allows us to develop a Hamiltonian Variational Auto-Encoder (HVAE). This method can be reinterpreted as a target-informed normalizing flow [20] which, within our context, only requires a few evaluations of the gradient of the sampled likelihood and trivial Jacobian calculations at each iteration.

Filtering Variational Objectives

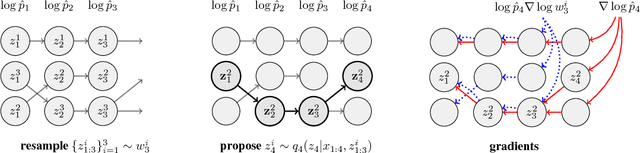
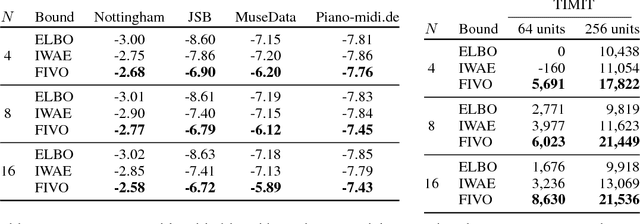
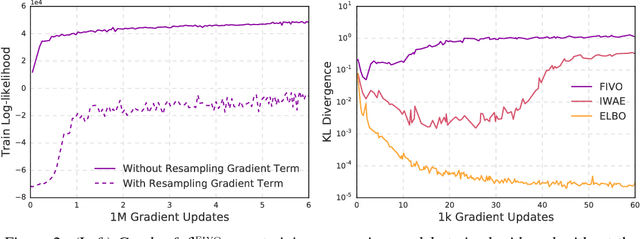
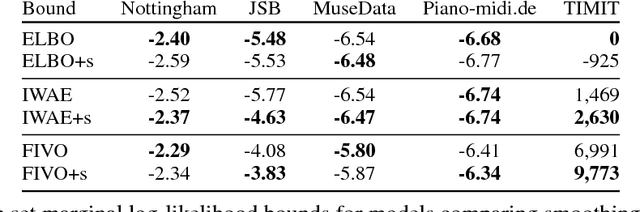
When used as a surrogate objective for maximum likelihood estimation in latent variable models, the evidence lower bound (ELBO) produces state-of-the-art results. Inspired by this, we consider the extension of the ELBO to a family of lower bounds defined by a particle filter's estimator of the marginal likelihood, the filtering variational objectives (FIVOs). FIVOs take the same arguments as the ELBO, but can exploit a model's sequential structure to form tighter bounds. We present results that relate the tightness of FIVO's bound to the variance of the particle filter's estimator by considering the generic case of bounds defined as log-transformed likelihood estimators. Experimentally, we show that training with FIVO results in substantial improvements over training the same model architecture with the ELBO on sequential data.

Asymptotic Bias of Stochastic Gradient Search

The asymptotic behavior of the stochastic gradient algorithm with a biased gradient estimator is analyzed. Relying on arguments based on the dynamic system theory (chain-recurrence) and the differential geometry (Yomdin theorem and Lojasiewicz inequality), tight bounds on the asymptotic bias of the iterates generated by such an algorithm are derived. The obtained results hold under mild conditions and cover a broad class of high-dimensional nonlinear algorithms. Using these results, the asymptotic properties of the policy-gradient (reinforcement) learning and adaptive population Monte Carlo sampling are studied. Relying on the same results, the asymptotic behavior of the recursive maximum split-likelihood estimation in hidden Markov models is analyzed, too.

Interacting Particle Markov Chain Monte Carlo

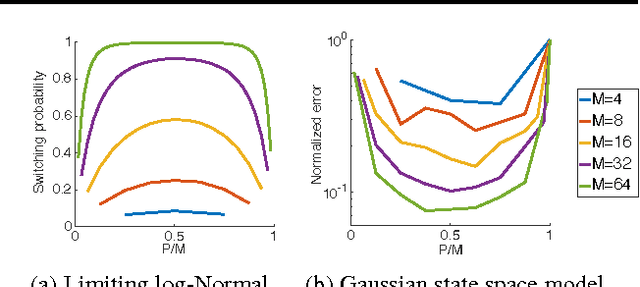
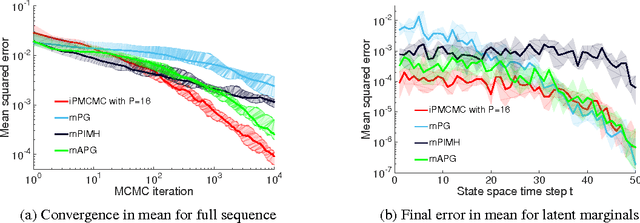
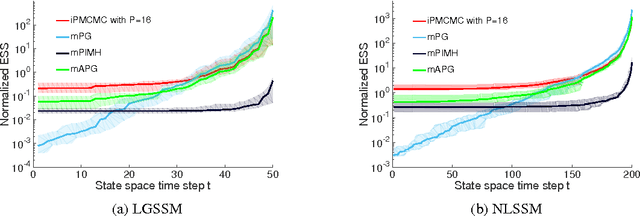
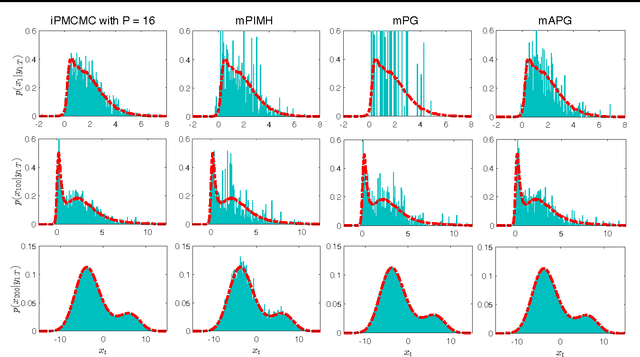
We introduce interacting particle Markov chain Monte Carlo (iPMCMC), a PMCMC method based on an interacting pool of standard and conditional sequential Monte Carlo samplers. Like related methods, iPMCMC is a Markov chain Monte Carlo sampler on an extended space. We present empirical results that show significant improvements in mixing rates relative to both non-interacting PMCMC samplers, and a single PMCMC sampler with an equivalent memory and computational budget. An additional advantage of the iPMCMC method is that it is suitable for distributed and multi-core architectures.

Particle Value Functions

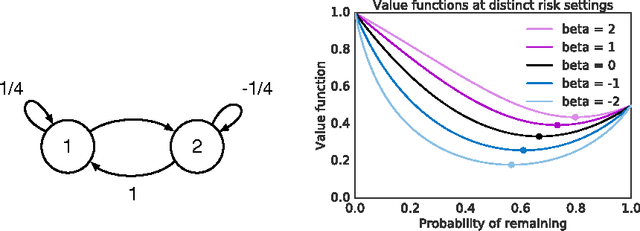
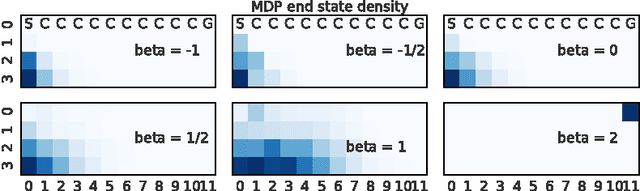
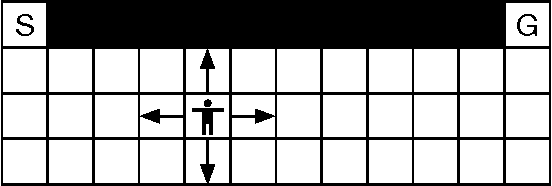
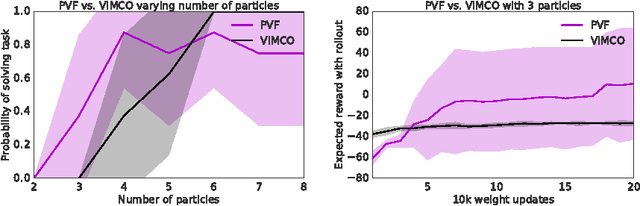
The policy gradients of the expected return objective can react slowly to rare rewards. Yet, in some cases agents may wish to emphasize the low or high returns regardless of their probability. Borrowing from the economics and control literature, we review the risk-sensitive value function that arises from an exponential utility and illustrate its effects on an example. This risk-sensitive value function is not always applicable to reinforcement learning problems, so we introduce the particle value function defined by a particle filter over the distributions of an agent's experience, which bounds the risk-sensitive one. We illustrate the benefit of the policy gradients of this objective in Cliffworld.