Alternate Loss Functions Can Improve the Performance of Artificial Neural Networks

All machine learning algorithms use a loss, cost, utility or reward function to encode the learning objective and oversee the learning process. This function that supervises learning is a frequently unrecognized hyperparameter that determines how incorrect outputs are penalized and can be tuned to improve performance. This paper shows that training speed and final accuracy of neural networks can significantly depend on the loss function used to train neural networks. In particular derivative values can be significantly different with different loss functions leading to significantly different performance after gradient descent based Backpropagation (BP) training. This paper explores the effect on performance of new loss functions that are more liberal or strict compared to the popular Cross-entropy loss in penalizing incorrect outputs. Eight new loss functions are proposed and a comparison of performance with different loss functions is presented. The new loss functions presented in this paper are shown to outperform Cross-entropy loss on computer vision and NLP benchmarks.

Improved Algorithms for Neural Active Learning

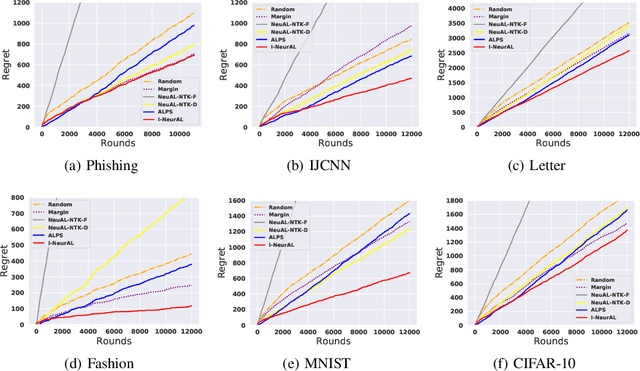
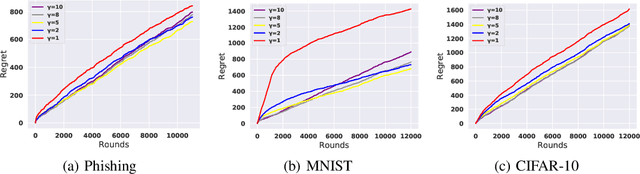
We improve the theoretical and empirical performance of neural-network(NN)-based active learning algorithms for the non-parametric streaming setting. In particular, we introduce two regret metrics by minimizing the population loss that are more suitable in active learning than the one used in state-of-the-art (SOTA) related work. Then, the proposed algorithm leverages the powerful representation of NNs for both exploitation and exploration, has the query decision-maker tailored for $k$-class classification problems with the performance guarantee, utilizes the full feedback, and updates parameters in a more practical and efficient manner. These careful designs lead to a better regret upper bound, improving by a multiplicative factor $O(\log T)$ and removing the curse of both input dimensionality and the complexity of the function to be learned. Furthermore, we show that the algorithm can achieve the same performance as the Bayes-optimal classifier in the long run under the hard-margin setting in classification problems. In the end, we use extensive experiments to evaluate the proposed algorithm and SOTA baselines, to show the improved empirical performance.

Restricted Strong Convexity of Deep Learning Models with Smooth Activations

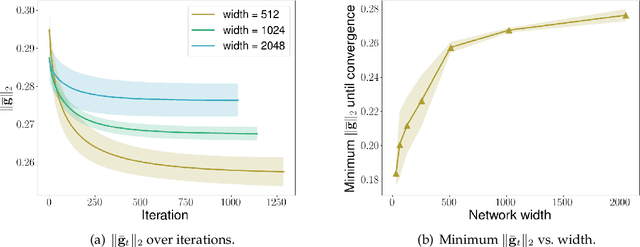
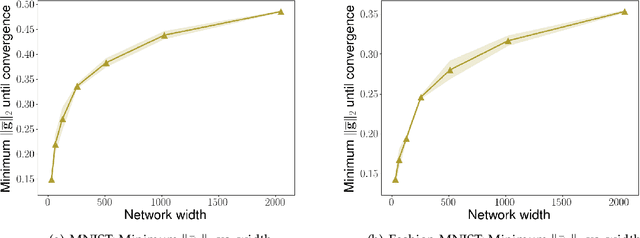
We consider the problem of optimization of deep learning models with smooth activation functions. While there exist influential results on the problem from the ``near initialization'' perspective, we shed considerable new light on the problem. In particular, we make two key technical contributions for such models with $L$ layers, $m$ width, and $\sigma_0^2$ initialization variance. First, for suitable $\sigma_0^2$, we establish a $O(\frac{\text{poly}(L)}{\sqrt{m}})$ upper bound on the spectral norm of the Hessian of such models, considerably sharpening prior results. Second, we introduce a new analysis of optimization based on Restricted Strong Convexity (RSC) which holds as long as the squared norm of the average gradient of predictors is $\Omega(\frac{\text{poly}(L)}{\sqrt{m}})$ for the square loss. We also present results for more general losses. The RSC based analysis does not need the ``near initialization" perspective and guarantees geometric convergence for gradient descent (GD). To the best of our knowledge, ours is the first result on establishing geometric convergence of GD based on RSC for deep learning models, thus becoming an alternative sufficient condition for convergence that does not depend on the widely-used Neural Tangent Kernel (NTK). We share preliminary experimental results supporting our theoretical advances.

Stability Based Generalization Bounds for Exponential Family Langevin Dynamics

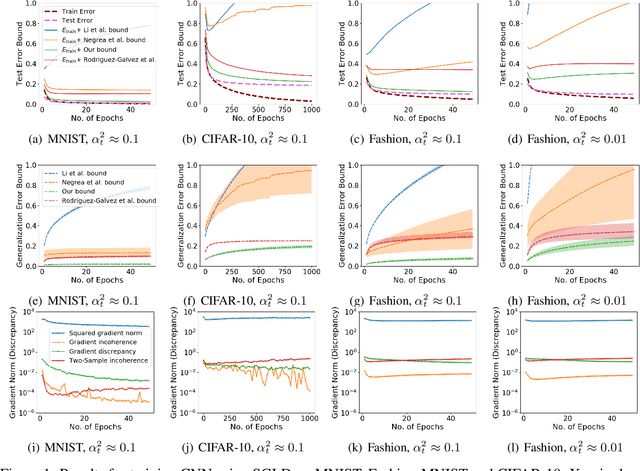
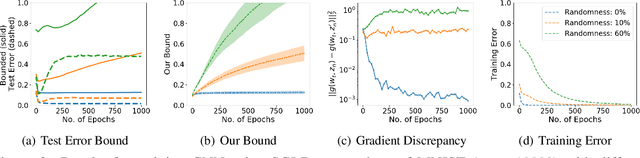
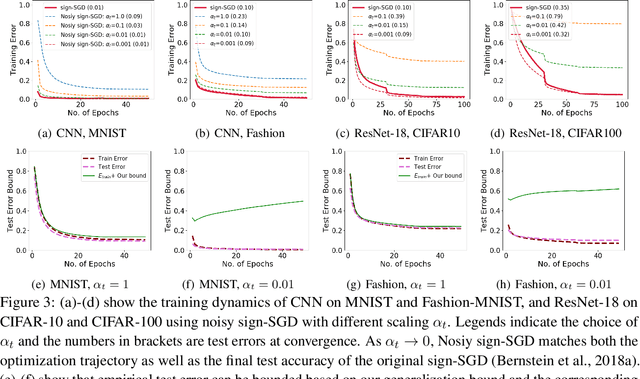
We study generalization bounds for noisy stochastic mini-batch iterative algorithms based on the notion of stability. Recent years have seen key advances in data-dependent generalization bounds for noisy iterative learning algorithms such as stochastic gradient Langevin dynamics (SGLD) based on stability (Mou et al., 2018; Li et al., 2020) and information theoretic approaches (Xu and Raginsky, 2017; Negrea et al., 2019; Steinke and Zakynthinou, 2020; Haghifam et al., 2020). In this paper, we unify and substantially generalize stability based generalization bounds and make three technical advances. First, we bound the generalization error of general noisy stochastic iterative algorithms (not necessarily gradient descent) in terms of expected (not uniform) stability. The expected stability can in turn be bounded by a Le Cam Style Divergence. Such bounds have a O(1/n) sample dependence unlike many existing bounds with O(1/\sqrt{n}) dependence. Second, we introduce Exponential Family Langevin Dynamics(EFLD) which is a substantial generalization of SGLD and which allows exponential family noise to be used with stochastic gradient descent (SGD). We establish data-dependent expected stability based generalization bounds for general EFLD algorithms. Third, we consider an important special case of EFLD: noisy sign-SGD, which extends sign-SGD using Bernoulli noise over {-1,+1}. Generalization bounds for noisy sign-SGD are implied by that of EFLD and we also establish optimization guarantees for the algorithm. Further, we present empirical results on benchmark datasets to illustrate that our bounds are non-vacuous and quantitatively much sharper than existing bounds.

TorchGeo: deep learning with geospatial data

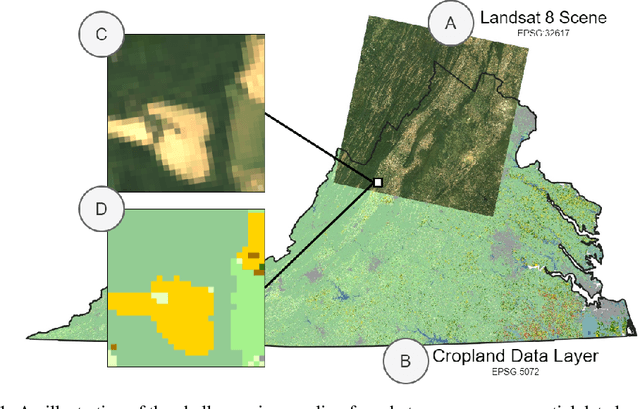
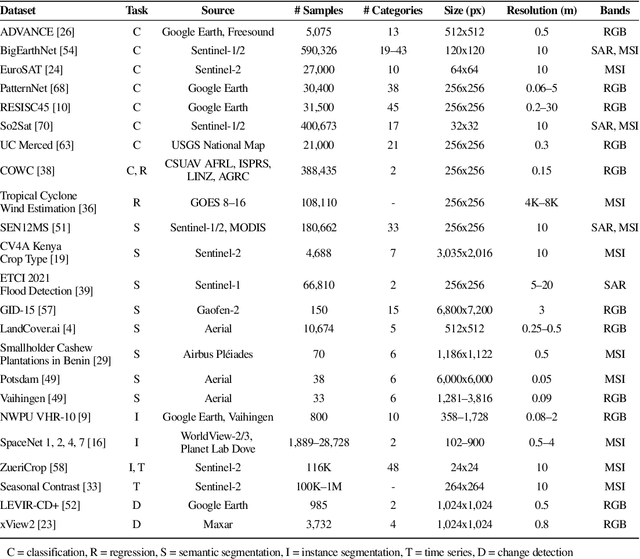
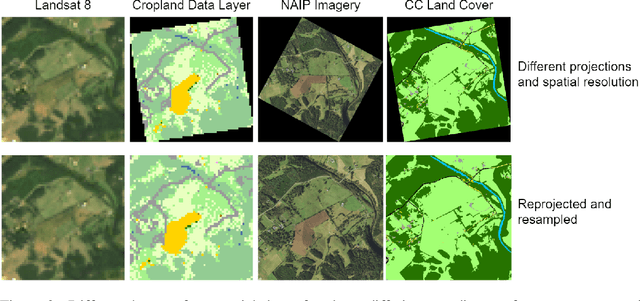
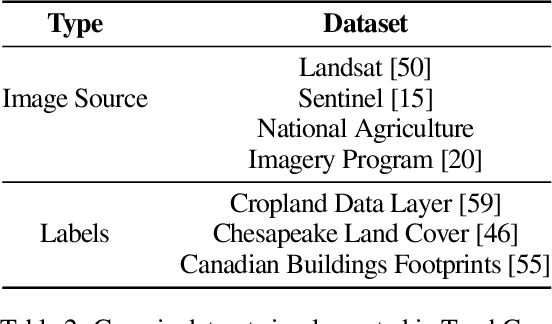
Remotely sensed geospatial data are critical for applications including precision agriculture, urban planning, disaster monitoring and response, and climate change research, among others. Deep learning methods are particularly promising for modeling many remote sensing tasks given the success of deep neural networks in similar computer vision tasks and the sheer volume of remotely sensed imagery available. However, the variance in data collection methods and handling of geospatial metadata make the application of deep learning methodology to remotely sensed data nontrivial. For example, satellite imagery often includes additional spectral bands beyond red, green, and blue and must be joined to other geospatial data sources that can have differing coordinate systems, bounds, and resolutions. To help realize the potential of deep learning for remote sensing applications, we introduce TorchGeo, a Python library for integrating geospatial data into the PyTorch deep learning ecosystem. TorchGeo provides data loaders for a variety of benchmark datasets, composable datasets for generic geospatial data sources, samplers for geospatial data, and transforms that work with multispectral imagery. TorchGeo is also the first library to provide pre-trained models for multispectral satellite imagery (e.g. models that use all bands from the Sentinel 2 satellites), allowing for advances in transfer learning on downstream remote sensing tasks with limited labeled data. We use TorchGeo to create reproducible benchmark results on existing datasets and benchmark our proposed method for preprocessing geospatial imagery on-the-fly. TorchGeo is open-source and available on GitHub: https://github.com/microsoft/torchgeo.

EE-Net: Exploitation-Exploration Neural Networks in Contextual Bandits

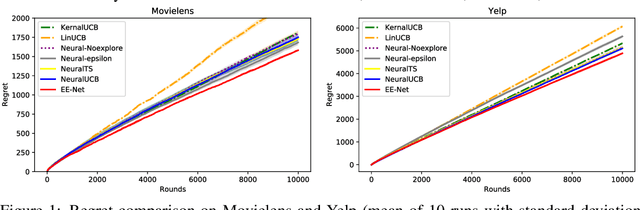
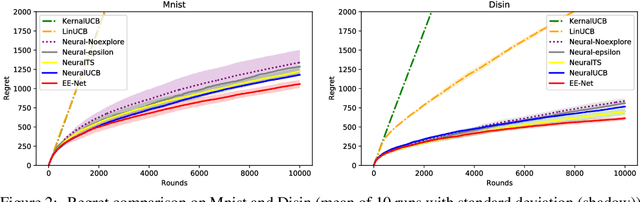
Contextual multi-armed bandits have been studied for decades and adapted to various applications such as online advertising and personalized recommendation. To solve the exploitation-exploration tradeoff in bandits, there are three main techniques: epsilon-greedy, Thompson Sampling (TS), and Upper Confidence Bound (UCB). In recent literature, linear contextual bandits have adopted ridge regression to estimate the reward function and combine it with TS or UCB strategies for exploration. However, this line of works explicitly assumes the reward is based on a linear function of arm vectors, which may not be true in real-world datasets. To overcome this challenge, a series of neural-based bandit algorithms have been proposed, where a neural network is assigned to learn the underlying reward function and TS or UCB are adapted for exploration. In this paper, we propose "EE-Net", a neural-based bandit approach with a novel exploration strategy. In addition to utilizing a neural network (Exploitation network) to learn the reward function, EE-Net adopts another neural network (Exploration network) to adaptively learn potential gains compared to currently estimated reward. Then, a decision-maker is constructed to combine the outputs from the Exploitation and Exploration networks. We prove that EE-Net achieves $\mathcal{O}(\sqrt{T\log T})$ regret, which is tighter than existing state-of-the-art neural bandit algorithms ($\mathcal{O}(\sqrt{T}\log T)$ for both UCB-based and TS-based). Through extensive experiments on four real-world datasets, we show that EE-Net outperforms existing linear and neural bandit approaches.

Learning and Dynamical Models for Sub-seasonal Climate Forecasting: Comparison and Collaboration

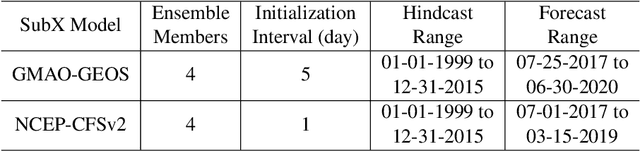
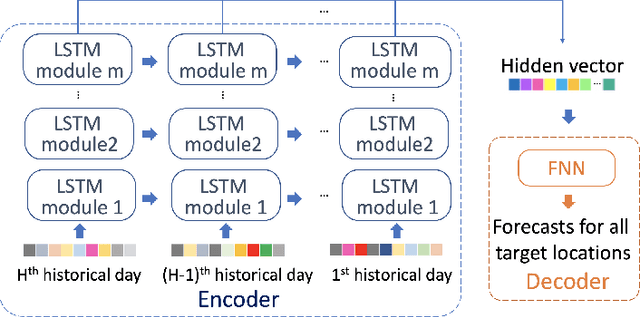
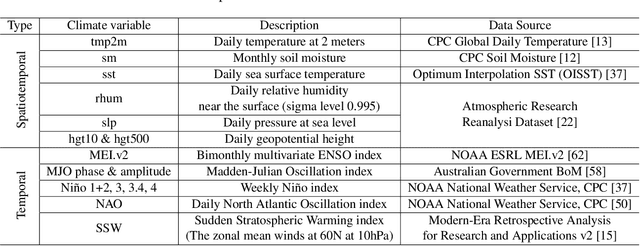
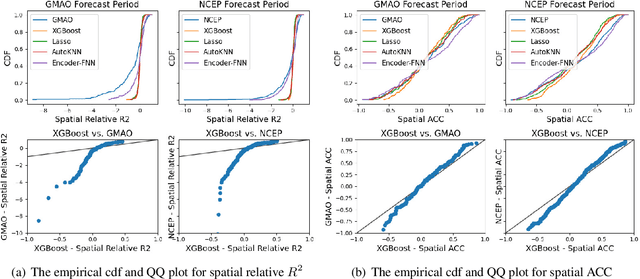
Sub-seasonal climate forecasting (SSF) is the prediction of key climate variables such as temperature and precipitation on the 2-week to 2-month time horizon. Skillful SSF would have substantial societal value in areas such as agricultural productivity, hydrology and water resource management, and emergency planning for extreme events such as droughts and wildfires. Despite its societal importance, SSF has stayed a challenging problem compared to both short-term weather forecasting and long-term seasonal forecasting. Recent studies have shown the potential of machine learning (ML) models to advance SSF. In this paper, for the first time, we perform a fine-grained comparison of a suite of modern ML models with start-of-the-art physics-based dynamical models from the Subseasonal Experiment (SubX) project for SSF in the western contiguous United States. Additionally, we explore mechanisms to enhance the ML models by using forecasts from dynamical models. Empirical results illustrate that, on average, ML models outperform dynamical models while the ML models tend to be conservatives in their forecasts compared to the SubX models. Further, we illustrate that ML models make forecasting errors under extreme weather conditions, e.g., cold waves due to the polar vortex, highlighting the need for separate models for extreme events. Finally, we show that suitably incorporating dynamical model forecasts as inputs to ML models can substantially improve the forecasting performance of the ML models. The SSF dataset constructed for the work, dynamical model predictions, and code for the ML models are released along with the paper for the benefit of the broader machine learning community.

Noisy Truncated SGD: Optimization and Generalization

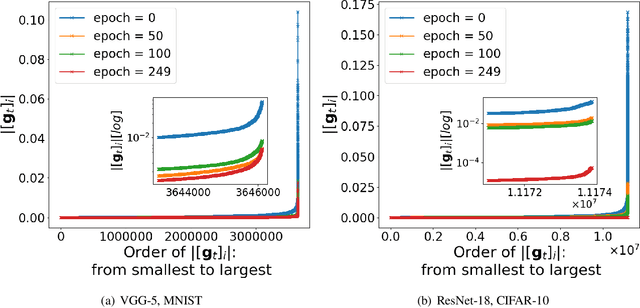
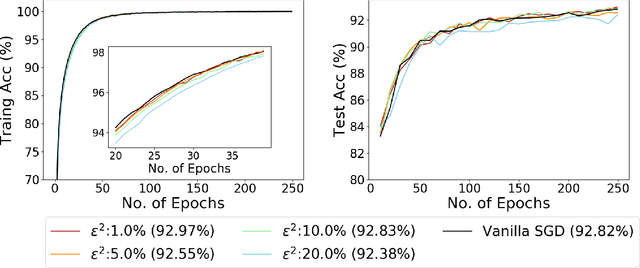
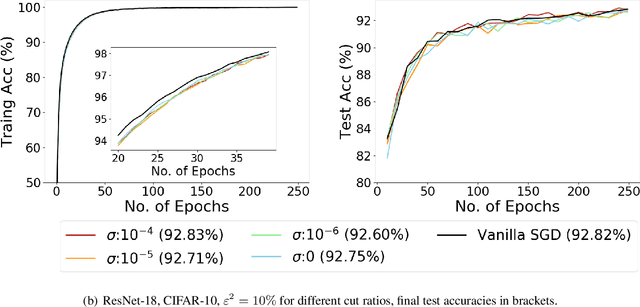
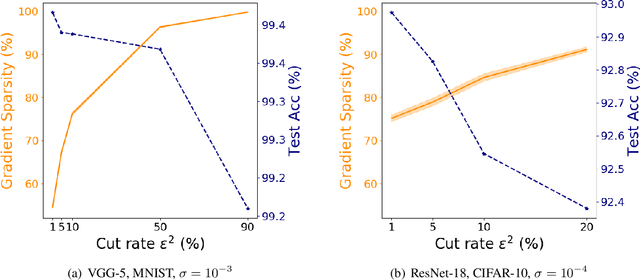
Recent empirical work on SGD applied to over-parameterized deep learning has shown that most gradient components over epochs are quite small. Inspired by such observations, we rigorously study properties of noisy truncated SGD (NT-SGD), a noisy gradient descent algorithm that truncates (hard thresholds) the majority of small gradient components to zeros and then adds Gaussian noise to all components. Considering non-convex smooth problems, we first establish the rate of convergence of NT-SGD in terms of empirical gradient norms, and show the rate to be of the same order as the vanilla SGD. Further, we prove that NT-SGD can provably escape from saddle points and requires less noise compared to previous related work. We also establish a generalization bound for NT-SGD using uniform stability based on discretized generalized Langevin dynamics. Our experiments on MNIST (VGG-5) and CIFAR-10 (ResNet-18) demonstrate that NT-SGD matches the speed and accuracy of vanilla SGD, and can successfully escape sharp minima while having better theoretical properties.

Experiments with Rich Regime Training for Deep Learning

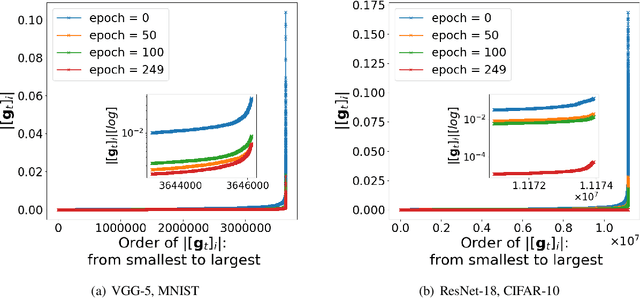
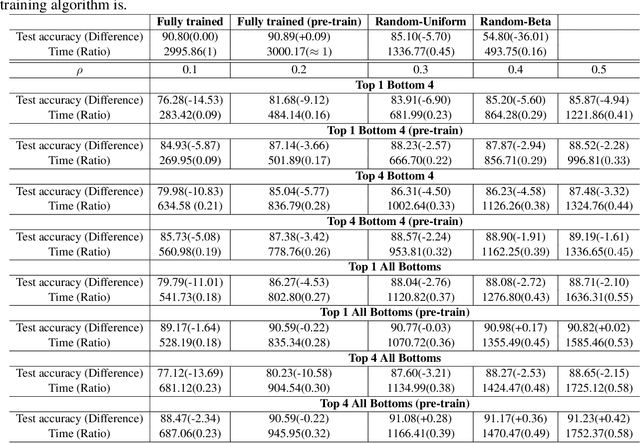
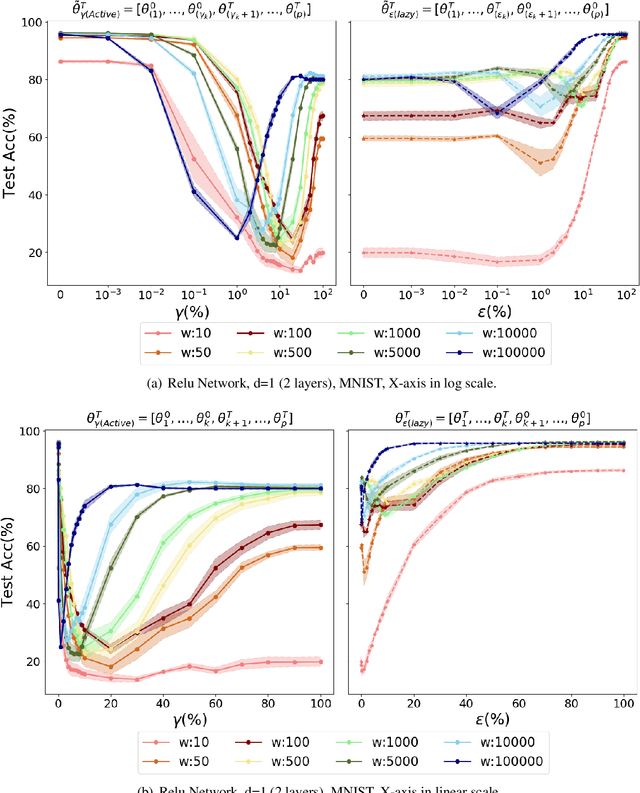
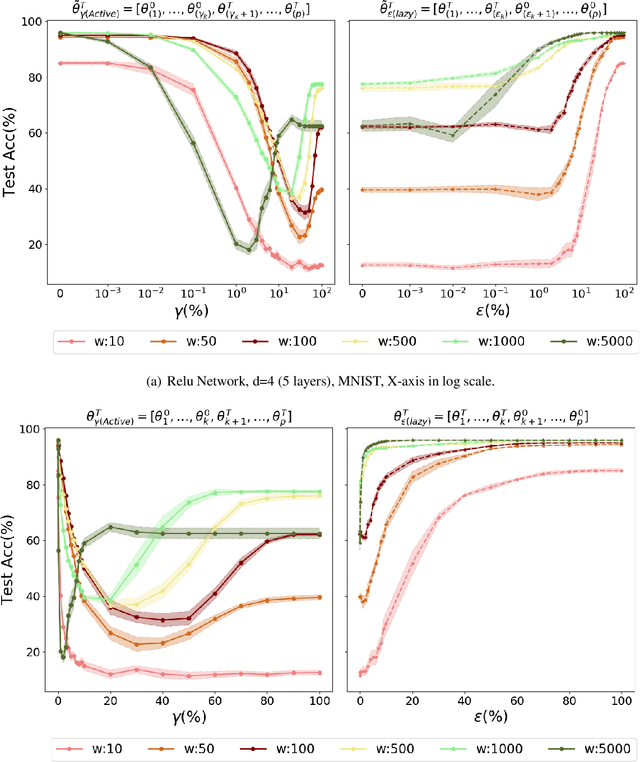
In spite of advances in understanding lazy training, recent work attributes the practical success of deep learning to the rich regime with complex inductive bias. In this paper, we study rich regime training empirically with benchmark datasets, and find that while most parameters are lazy, there is always a small number of active parameters which change quite a bit during training. We show that re-initializing (resetting to their initial random values) the active parameters leads to worse generalization. Further, we show that most of the active parameters are in the bottom layers, close to the input, especially as the networks become wider. Based on such observations, we study static Layer-Wise Sparse (LWS) SGD, which only updates some subsets of layers. We find that only updating the top and bottom layers have good generalization and, as expected, only updating the top layers yields a fast algorithm. Inspired by this, we investigate probabilistic LWS-SGD, which mostly updates the top layers and occasionally updates the full network. We show that probabilistic LWS-SGD matches the generalization performance of vanilla SGD and the back-propagation time can be 2-5 times more efficient.

Bypassing the Ambient Dimension: Private SGD with Gradient Subspace Identification

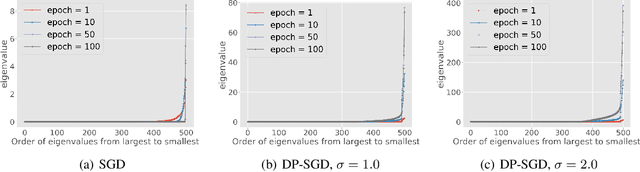
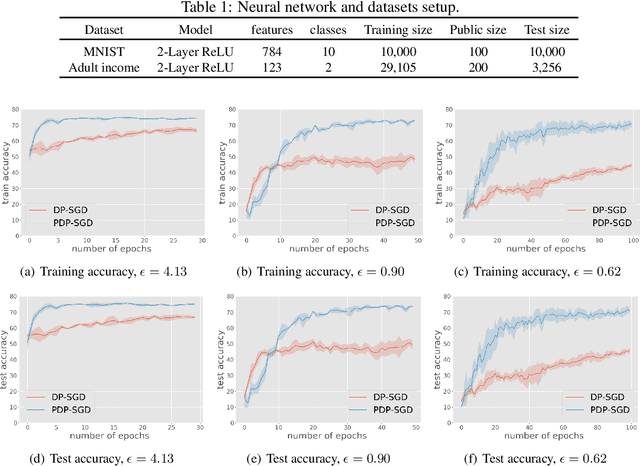
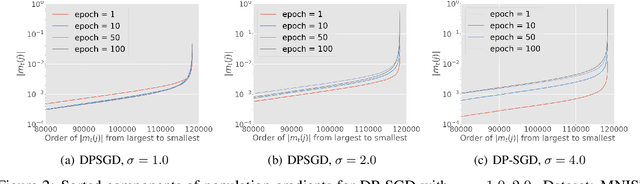
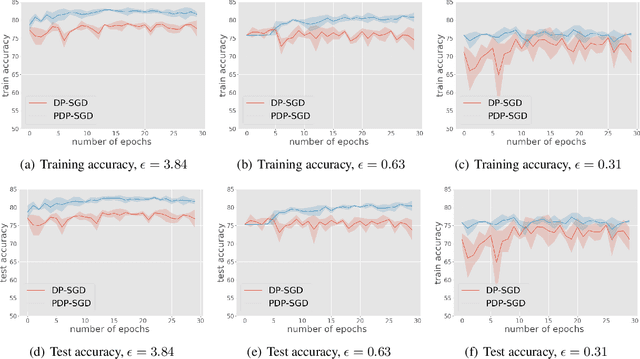
Differentially private SGD (DP-SGD) is one of the most popular methods for solving differentially private empirical risk minimization (ERM). Due to its noisy perturbation on each gradient update, the error rate of DP-SGD scales with the ambient dimension $p$, the number of parameters in the model. Such dependence can be problematic for over-parameterized models where $p \gg n$, the number of training samples. Existing lower bounds on private ERM show that such dependence on $p$ is inevitable in the worst case. In this paper, we circumvent the dependence on the ambient dimension by leveraging a low-dimensional structure of gradient space in deep networks---that is, the stochastic gradients for deep nets usually stay in a low dimensional subspace in the training process. We propose Projected DP-SGD that performs noise reduction by projecting the noisy gradients to a low-dimensional subspace, which is given by the top gradient eigenspace on a small public dataset. We provide a general sample complexity analysis on the public dataset for the gradient subspace identification problem and demonstrate that under certain low-dimensional assumptions the public sample complexity only grows logarithmically in $p$. Finally, we provide a theoretical analysis and empirical evaluations to show that our method can substantially improve the accuracy of DP-SGD.