High-Dimensional Covariance Decomposition into Sparse Markov and Independence Domains

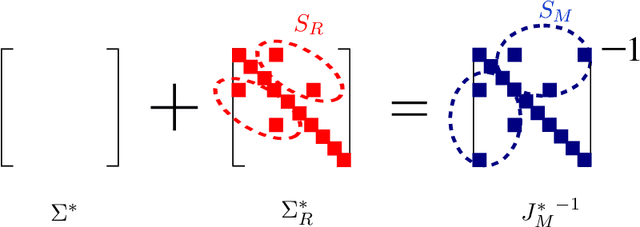
In this paper, we present a novel framework incorporating a combination of sparse models in different domains. We posit the observed data as generated from a linear combination of a sparse Gaussian Markov model (with a sparse precision matrix) and a sparse Gaussian independence model (with a sparse covariance matrix). We provide efficient methods for decomposition of the data into two domains, \viz Markov and independence domains. We characterize a set of sufficient conditions for identifiability and model consistency. Our decomposition method is based on a simple modification of the popular $\ell_1$-penalized maximum-likelihood estimator ($\ell_1$-MLE). We establish that our estimator is consistent in both the domains, i.e., it successfully recovers the supports of both Markov and independence models, when the number of samples $n$ scales as $n = \Omega(d^2 \log p)$, where $p$ is the number of variables and $d$ is the maximum node degree in the Markov model. Our conditions for recovery are comparable to those of $\ell_1$-MLE for consistent estimation of a sparse Markov model, and thus, we guarantee successful high-dimensional estimation of a richer class of models under comparable conditions. Our experiments validate these results and also demonstrate that our models have better inference accuracy under simple algorithms such as loopy belief propagation.

High-Dimensional Gaussian Graphical Model Selection: Walk Summability and Local Separation Criterion

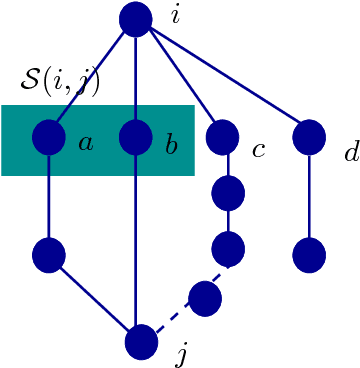
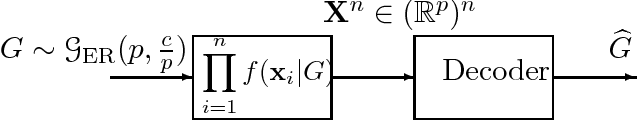
We consider the problem of high-dimensional Gaussian graphical model selection. We identify a set of graphs for which an efficient estimation algorithm exists, and this algorithm is based on thresholding of empirical conditional covariances. Under a set of transparent conditions, we establish structural consistency (or sparsistency) for the proposed algorithm, when the number of samples n=omega(J_{min}^{-2} log p), where p is the number of variables and J_{min} is the minimum (absolute) edge potential of the graphical model. The sufficient conditions for sparsistency are based on the notion of walk-summability of the model and the presence of sparse local vertex separators in the underlying graph. We also derive novel non-asymptotic necessary conditions on the number of samples required for sparsistency.

Spectral Methods for Learning Multivariate Latent Tree Structure

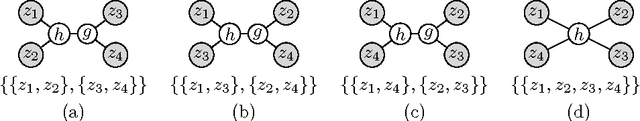
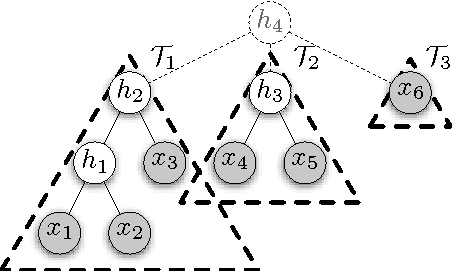
This work considers the problem of learning the structure of multivariate linear tree models, which include a variety of directed tree graphical models with continuous, discrete, and mixed latent variables such as linear-Gaussian models, hidden Markov models, Gaussian mixture models, and Markov evolutionary trees. The setting is one where we only have samples from certain observed variables in the tree, and our goal is to estimate the tree structure (i.e., the graph of how the underlying hidden variables are connected to each other and to the observed variables). We propose the Spectral Recursive Grouping algorithm, an efficient and simple bottom-up procedure for recovering the tree structure from independent samples of the observed variables. Our finite sample size bounds for exact recovery of the tree structure reveal certain natural dependencies on underlying statistical and structural properties of the underlying joint distribution. Furthermore, our sample complexity guarantees have no explicit dependence on the dimensionality of the observed variables, making the algorithm applicable to many high-dimensional settings. At the heart of our algorithm is a spectral quartet test for determining the relative topology of a quartet of variables from second-order statistics.

Feedback Message Passing for Inference in Gaussian Graphical Models

While loopy belief propagation (LBP) performs reasonably well for inference in some Gaussian graphical models with cycles, its performance is unsatisfactory for many others. In particular for some models LBP does not converge, and in general when it does converge, the computed variances are incorrect (except for cycle-free graphs for which belief propagation (BP) is non-iterative and exact). In this paper we propose {\em feedback message passing} (FMP), a message-passing algorithm that makes use of a special set of vertices (called a {\em feedback vertex set} or {\em FVS}) whose removal results in a cycle-free graph. In FMP, standard BP is employed several times on the cycle-free subgraph excluding the FVS while a special message-passing scheme is used for the nodes in the FVS. The computational complexity of exact inference is $O(k^2n)$, where $k$ is the number of feedback nodes, and $n$ is the total number of nodes. When the size of the FVS is very large, FMP is intractable. Hence we propose {\em approximate FMP}, where a pseudo-FVS is used instead of an FVS, and where inference in the non-cycle-free graph obtained by removing the pseudo-FVS is carried out approximately using LBP. We show that, when approximate FMP converges, it yields exact means and variances on the pseudo-FVS and exact means throughout the remainder of the graph. We also provide theoretical results on the convergence and accuracy of approximate FMP. In particular, we prove error bounds on variance computation. Based on these theoretical results, we design efficient algorithms to select a pseudo-FVS of bounded size. The choice of the pseudo-FVS allows us to explicitly trade off between efficiency and accuracy. Experimental results show that using a pseudo-FVS of size no larger than $\log(n)$, this procedure converges much more often, more quickly, and provides more accurate results than LBP on the entire graph.

Learning High-Dimensional Markov Forest Distributions: Analysis of Error Rates

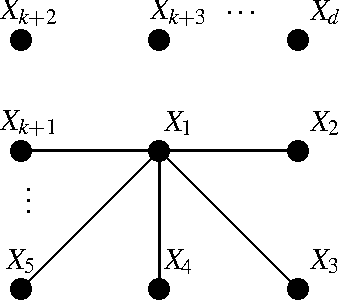
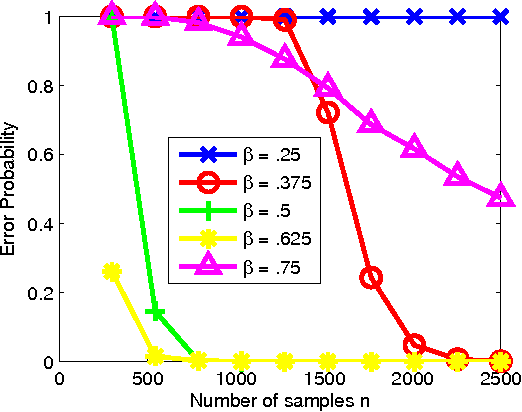
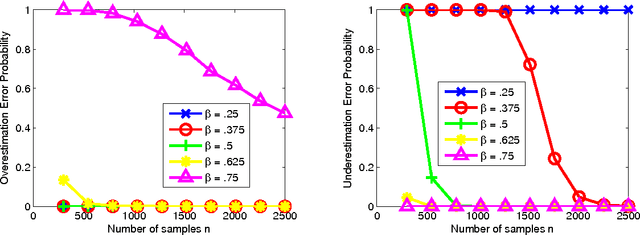
The problem of learning forest-structured discrete graphical models from i.i.d. samples is considered. An algorithm based on pruning of the Chow-Liu tree through adaptive thresholding is proposed. It is shown that this algorithm is both structurally consistent and risk consistent and the error probability of structure learning decays faster than any polynomial in the number of samples under fixed model size. For the high-dimensional scenario where the size of the model d and the number of edges k scale with the number of samples n, sufficient conditions on (n,d,k) are given for the algorithm to satisfy structural and risk consistencies. In addition, the extremal structures for learning are identified; we prove that the independent (resp. tree) model is the hardest (resp. easiest) to learn using the proposed algorithm in terms of error rates for structure learning.

A Large-Deviation Analysis of the Maximum-Likelihood Learning of Markov Tree Structures

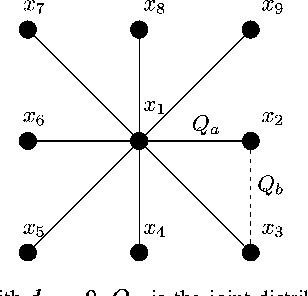
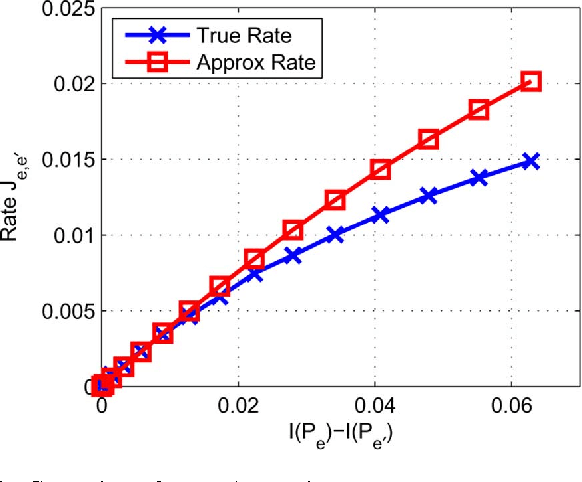
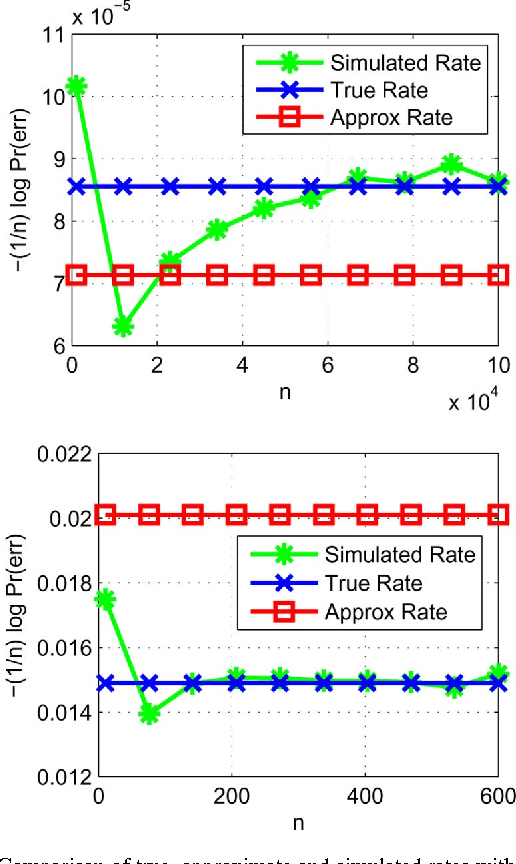
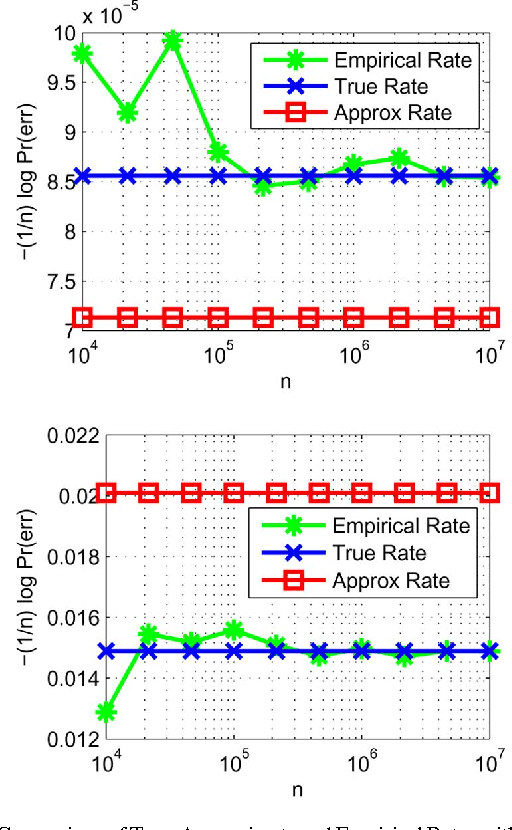
The problem of maximum-likelihood (ML) estimation of discrete tree-structured distributions is considered. Chow and Liu established that ML-estimation reduces to the construction of a maximum-weight spanning tree using the empirical mutual information quantities as the edge weights. Using the theory of large-deviations, we analyze the exponent associated with the error probability of the event that the ML-estimate of the Markov tree structure differs from the true tree structure, given a set of independently drawn samples. By exploiting the fact that the output of ML-estimation is a tree, we establish that the error exponent is equal to the exponential rate of decay of a single dominant crossover event. We prove that in this dominant crossover event, a non-neighbor node pair replaces a true edge of the distribution that is along the path of edges in the true tree graph connecting the nodes in the non-neighbor pair. Using ideas from Euclidean information theory, we then analyze the scenario of ML-estimation in the very noisy learning regime and show that the error exponent can be approximated as a ratio, which is interpreted as the signal-to-noise ratio (SNR) for learning tree distributions. We show via numerical experiments that in this regime, our SNR approximation is accurate.

Learning Latent Tree Graphical Models

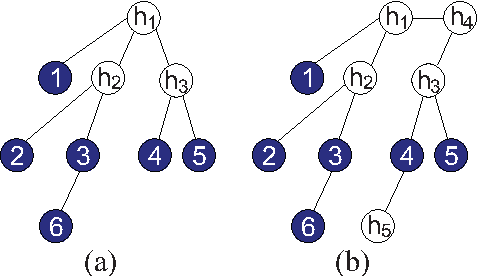
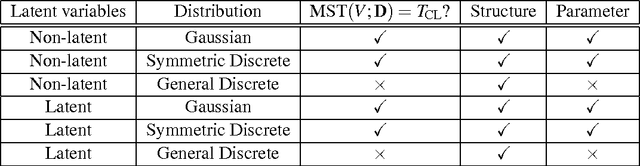
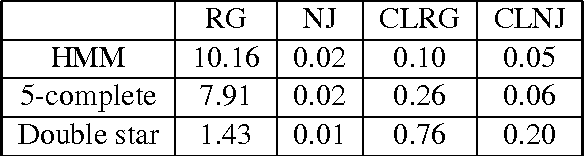
We study the problem of learning a latent tree graphical model where samples are available only from a subset of variables. We propose two consistent and computationally efficient algorithms for learning minimal latent trees, that is, trees without any redundant hidden nodes. Unlike many existing methods, the observed nodes (or variables) are not constrained to be leaf nodes. Our first algorithm, recursive grouping, builds the latent tree recursively by identifying sibling groups using so-called information distances. One of the main contributions of this work is our second algorithm, which we refer to as CLGrouping. CLGrouping starts with a pre-processing procedure in which a tree over the observed variables is constructed. This global step groups the observed nodes that are likely to be close to each other in the true latent tree, thereby guiding subsequent recursive grouping (or equivalent procedures) on much smaller subsets of variables. This results in more accurate and efficient learning of latent trees. We also present regularized versions of our algorithms that learn latent tree approximations of arbitrary distributions. We compare the proposed algorithms to other methods by performing extensive numerical experiments on various latent tree graphical models such as hidden Markov models and star graphs. In addition, we demonstrate the applicability of our methods on real-world datasets by modeling the dependency structure of monthly stock returns in the S&P index and of the words in the 20 newsgroups dataset.

Distributed Algorithms for Learning and Cognitive Medium Access with Logarithmic Regret

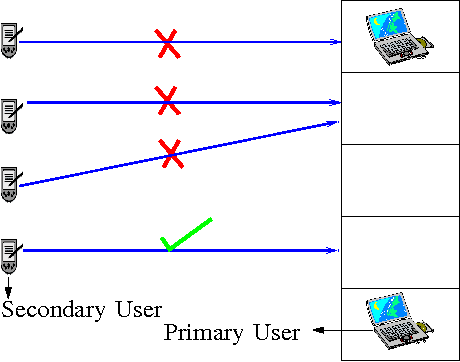
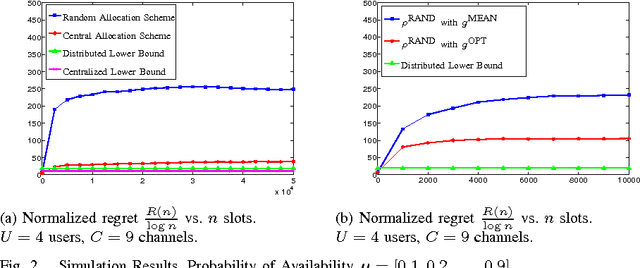
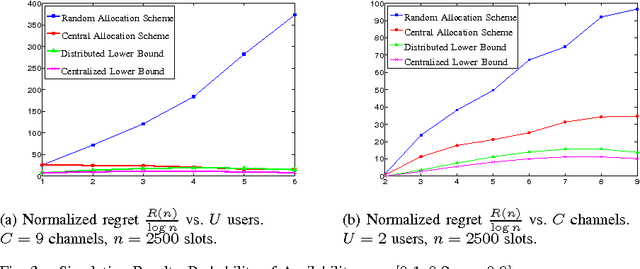
The problem of distributed learning and channel access is considered in a cognitive network with multiple secondary users. The availability statistics of the channels are initially unknown to the secondary users and are estimated using sensing decisions. There is no explicit information exchange or prior agreement among the secondary users. We propose policies for distributed learning and access which achieve order-optimal cognitive system throughput (number of successful secondary transmissions) under self play, i.e., when implemented at all the secondary users. Equivalently, our policies minimize the regret in distributed learning and access. We first consider the scenario when the number of secondary users is known to the policy, and prove that the total regret is logarithmic in the number of transmission slots. Our distributed learning and access policy achieves order-optimal regret by comparing to an asymptotic lower bound for regret under any uniformly-good learning and access policy. We then consider the case when the number of secondary users is fixed but unknown, and is estimated through feedback. We propose a policy in this scenario whose asymptotic sum regret which grows slightly faster than logarithmic in the number of transmission slots.

Learning Gaussian Tree Models: Analysis of Error Exponents and Extremal Structures

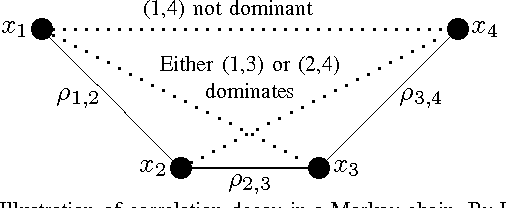
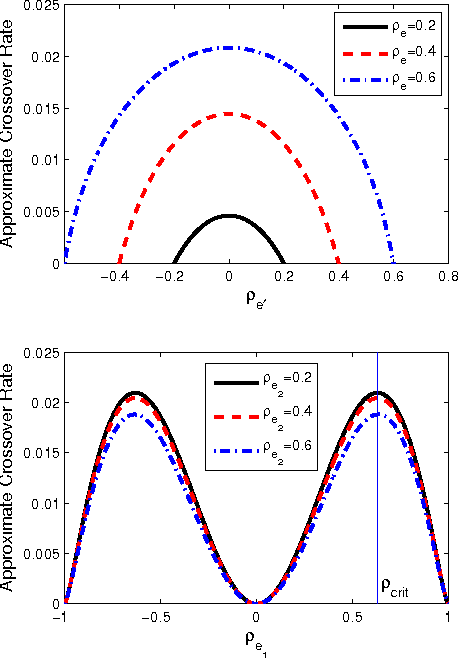
The problem of learning tree-structured Gaussian graphical models from independent and identically distributed (i.i.d.) samples is considered. The influence of the tree structure and the parameters of the Gaussian distribution on the learning rate as the number of samples increases is discussed. Specifically, the error exponent corresponding to the event that the estimated tree structure differs from the actual unknown tree structure of the distribution is analyzed. Finding the error exponent reduces to a least-squares problem in the very noisy learning regime. In this regime, it is shown that the extremal tree structure that minimizes the error exponent is the star for any fixed set of correlation coefficients on the edges of the tree. If the magnitudes of all the correlation coefficients are less than 0.63, it is also shown that the tree structure that maximizes the error exponent is the Markov chain. In other words, the star and the chain graphs represent the hardest and the easiest structures to learn in the class of tree-structured Gaussian graphical models. This result can also be intuitively explained by correlation decay: pairs of nodes which are far apart, in terms of graph distance, are unlikely to be mistaken as edges by the maximum-likelihood estimator in the asymptotic regime.