Universal Functional Regression with Neural Operator Flows

Regression on function spaces is typically limited to models with Gaussian process priors. We introduce the notion of universal functional regression, in which we aim to learn a prior distribution over non-Gaussian function spaces that remains mathematically tractable for functional regression. To do this, we develop Neural Operator Flows (OpFlow), an infinite-dimensional extension of normalizing flows. OpFlow is an invertible operator that maps the (potentially unknown) data function space into a Gaussian process, allowing for exact likelihood estimation of functional point evaluations. OpFlow enables robust and accurate uncertainty quantification via drawing posterior samples of the Gaussian process and subsequently mapping them into the data function space. We empirically study the performance of OpFlow on regression and generation tasks with data generated from Gaussian processes with known posterior forms and non-Gaussian processes, as well as real-world earthquake seismograms with an unknown closed-form distribution.

Ill-Posed Image Reconstruction Without an Image Prior

We consider solving ill-posed imaging inverse problems without access to an image prior or ground-truth examples. An overarching challenge in these inverse problems is that an infinite number of images, including many that are implausible, are consistent with the observed measurements. Thus, image priors are required to reduce the space of possible solutions to more desireable reconstructions. However, in many applications it is difficult or potentially impossible to obtain example images to construct an image prior. Hence inaccurate priors are often used, which inevitably result in biased solutions. Rather than solving an inverse problem using priors that encode the spatial structure of any one image, we propose to solve a set of inverse problems jointly by incorporating prior constraints on the collective structure of the underlying images. The key assumption of our work is that the underlying images we aim to reconstruct share common, low-dimensional structure. We show that such a set of inverse problems can be solved simultaneously without the use of a spatial image prior by instead inferring a shared image generator with a low-dimensional latent space. The parameters of the generator and latent embeddings are found by maximizing a proxy for the Evidence Lower Bound (ELBO). Once identified, the generator and latent embeddings can be combined to provide reconstructed images for each inverse problem. The framework we propose can handle general forward model corruptions, and we show that measurements derived from only a small number of ground-truth images ($\leqslant 150$) are sufficient for "prior-free" image reconstruction. We demonstrate our approach on a variety of convex and non-convex inverse problems, ranging from denoising, phase retrieval, and black hole video reconstruction.

Image Reconstruction without Explicit Priors

We consider solving ill-posed imaging inverse problems without access to an explicit image prior or ground-truth examples. An overarching challenge in inverse problems is that there are many undesired images that fit to the observed measurements, thus requiring image priors to constrain the space of possible solutions to more plausible reconstructions. However, in many applications it is difficult or potentially impossible to obtain ground-truth images to learn an image prior. Thus, inaccurate priors are often used, which inevitably result in biased solutions. Rather than solving an inverse problem using priors that encode the explicit structure of any one image, we propose to solve a set of inverse problems jointly by incorporating prior constraints on the collective structure of the underlying images.The key assumption of our work is that the ground-truth images we aim to reconstruct share common, low-dimensional structure. We show that such a set of inverse problems can be solved simultaneously by learning a shared image generator with a low-dimensional latent space. The parameters of the generator and latent embedding are learned by maximizing a proxy for the Evidence Lower Bound (ELBO). Once learned, the generator and latent embeddings can be combined to provide reconstructions for each inverse problem. The framework we propose can handle general forward model corruptions, and we show that measurements derived from only a few ground-truth images (O(10)) are sufficient for image reconstruction without explicit priors.

Seismic wave propagation and inversion with Neural Operators

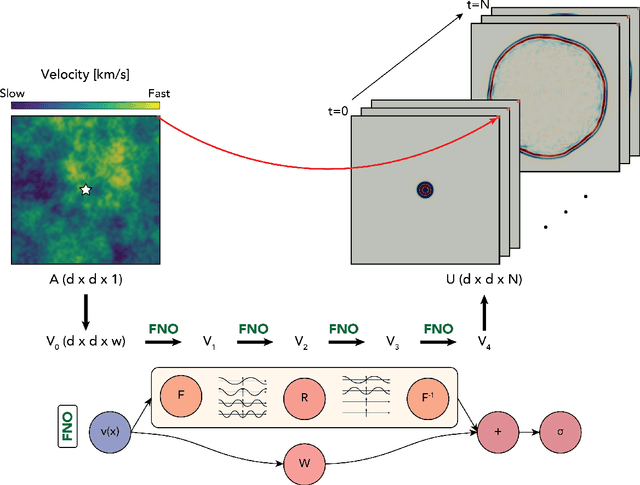
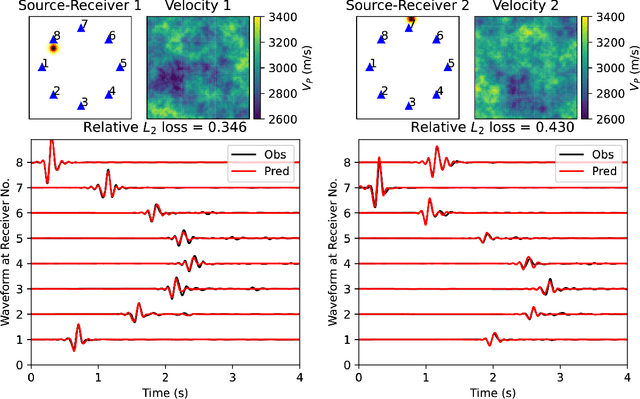
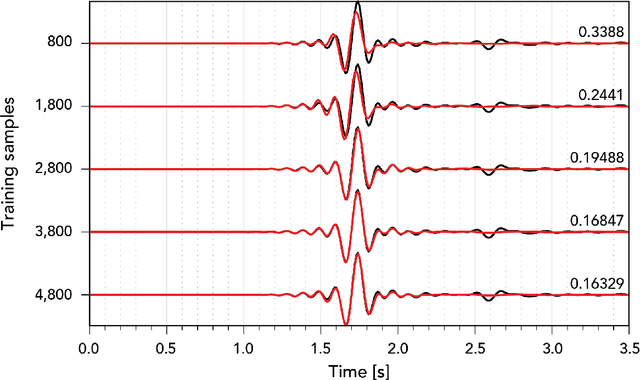
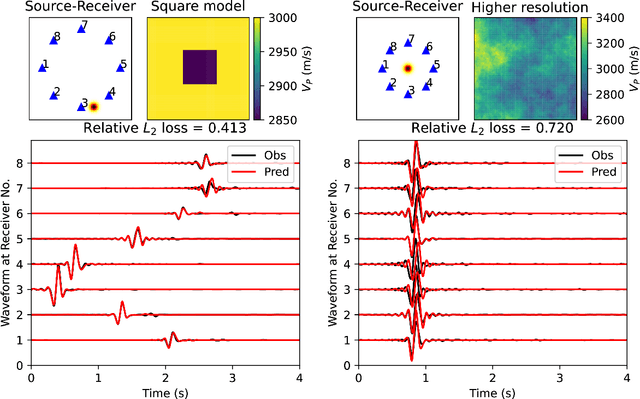
Seismic wave propagation forms the basis for most aspects of seismological research, yet solving the wave equation is a major computational burden that inhibits the progress of research. This is exaspirated by the fact that new simulations must be performed when the velocity structure or source location is perturbed. Here, we explore a prototype framework for learning general solutions using a recently developed machine learning paradigm called Neural Operator. A trained Neural Operator can compute a solution in negligible time for any velocity structure or source location. We develop a scheme to train Neural Operators on an ensemble of simulations performed with random velocity models and source locations. As Neural Operators are grid-free, it is possible to evaluate solutions on higher resolution velocity models than trained on, providing additional computational efficiency. We illustrate the method with the 2D acoustic wave equation and demonstrate the method's applicability to seismic tomography, using reverse mode automatic differentiation to compute gradients of the wavefield with respect to the velocity structure. The developed procedure is nearly an order of magnitude faster than using conventional numerical methods for full waveform inversion.

Generalized Unsupervised Clustering of Hyperspectral Images of Geological Targets in the Near Infrared

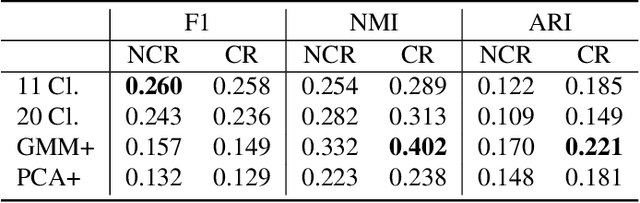
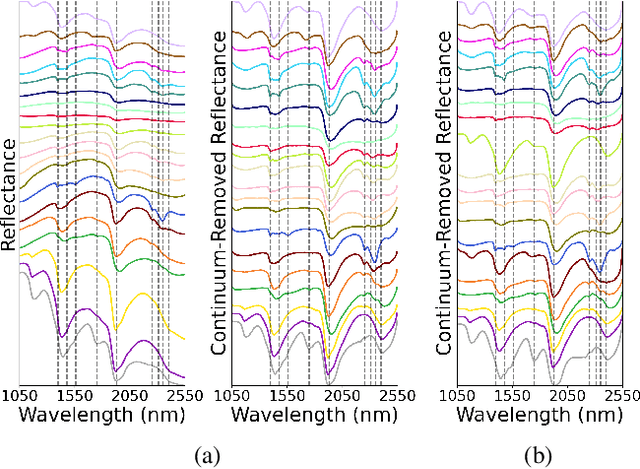
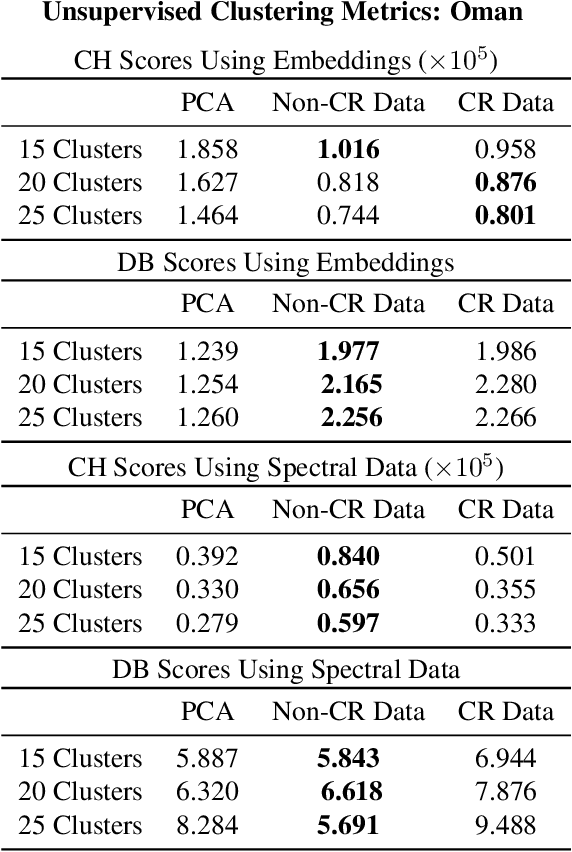
The application of infrared hyperspectral imagery to geological problems is becoming more popular as data become more accessible and cost-effective. Clustering and classifying spectrally similar materials is often a first step in applications ranging from economic mineral exploration on Earth to planetary exploration on Mars. Semi-manual classification guided by expertly developed spectral parameters can be time consuming and biased, while supervised methods require abundant labeled data and can be difficult to generalize. Here we develop a fully unsupervised workflow for feature extraction and clustering informed by both expert spectral geologist input and quantitative metrics. Our pipeline uses a lightweight autoencoder followed by Gaussian mixture modeling to map the spectral diversity within any image. We validate the performance of our pipeline at submillimeter-scale with expert-labelled data from the Oman ophiolite drill core and evaluate performance at meters-scale with partially classified orbital data of Jezero Crater on Mars (the landing site for the Perseverance rover). We additionally examine the effects of various preprocessing techniques used in traditional analysis of hyperspectral imagery. This pipeline provides a fast and accurate clustering map of similar geological materials and consistently identifies and separates major mineral classes in both laboratory imagery and remote sensing imagery. We refer to our pipeline as "Generalized Pipeline for Spectroscopic Unsupervised clustering of Minerals (GyPSUM)."