Accelerating Optimization and Reinforcement Learning with Quasi-Stochastic Approximation

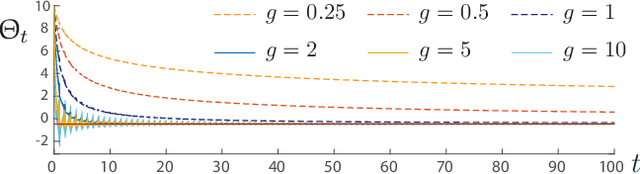
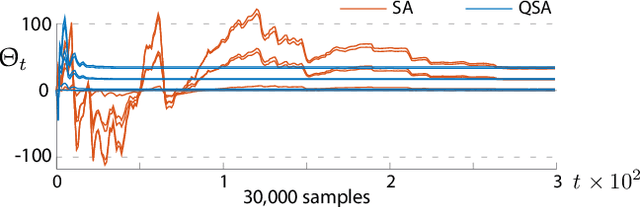
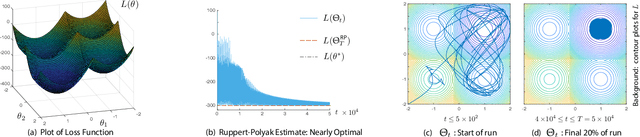
The ODE method has been a workhorse for algorithm design and analysis since the introduction of the stochastic approximation. It is now understood that convergence theory amounts to establishing robustness of Euler approximations for ODEs, while theory of rates of convergence requires finer analysis. This paper sets out to extend this theory to quasi-stochastic approximation, based on algorithms in which the "noise" is based on deterministic signals. The main results are obtained under minimal assumptions: the usual Lipschitz conditions for ODE vector fields, and it is assumed that there is a well defined linearization near the optimal parameter $\theta^*$, with Hurwitz linearization matrix $A^*$. The main contributions are summarized as follows: (i) If the algorithm gain is $a_t=g/(1+t)^\rho$ with $g>0$ and $\rho\in(0,1)$, then the rate of convergence of the algorithm is $1/t^\rho$. There is also a well defined "finite-$t$" approximation: \[ a_t^{-1}\{\Theta_t-\theta^*\}=\bar{Y}+\Xi^{\mathrm{I}}_t+o(1) \] where $\bar{Y}\in\mathbb{R}^d$ is a vector identified in the paper, and $\{\Xi^{\mathrm{I}}_t\}$ is bounded with zero temporal mean. (ii) With gain $a_t = g/(1+t)$ the results are not as sharp: the rate of convergence $1/t$ holds only if $I + g A^*$ is Hurwitz. (iii) Based on the Ruppert-Polyak averaging of stochastic approximation, one would expect that a convergence rate of $1/t$ can be obtained by averaging: \[ \Theta^{\text{RP}}_T=\frac{1}{T}\int_{0}^T \Theta_t\,dt \] where the estimates $\{\Theta_t\}$ are obtained using the gain in (i). The preceding sharp bounds imply that averaging results in $1/t$ convergence rate if and only if $\bar{Y}=\sf 0$. This condition holds if the noise is additive, but appears to fail in general. (iv) The theory is illustrated with applications to gradient-free optimization and policy gradient algorithms for reinforcement learning.

Model-Free State Estimation Using Low-Rank Canonical Polyadic Decomposition

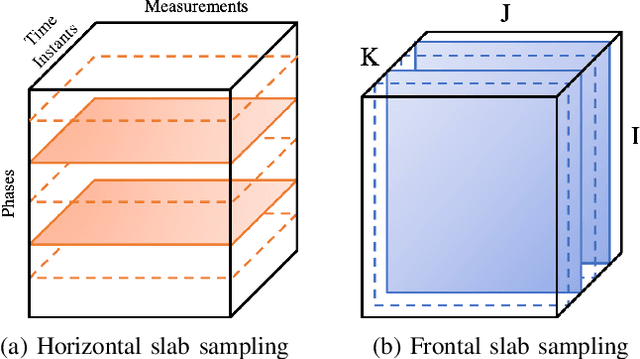
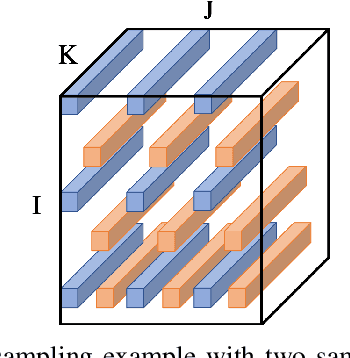
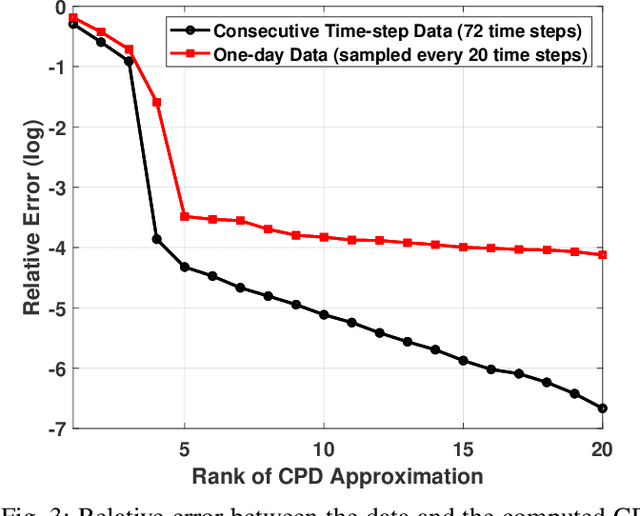
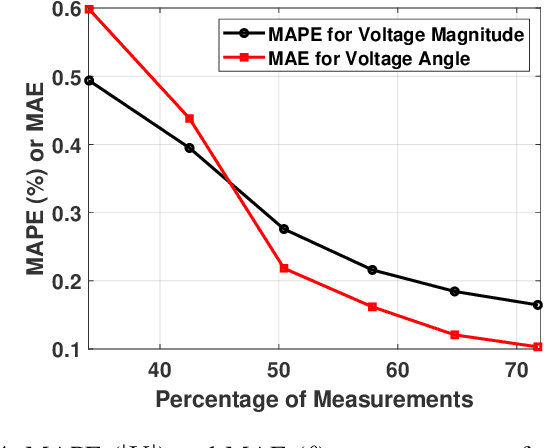
As electric grids experience high penetration levels of renewable generation, fundamental changes are required to address real-time situational awareness. This paper uses unique traits of tensors to devise a model-free situational awareness and energy forecasting framework for distribution networks. This work formulates the state of the network at multiple time instants as a three-way tensor; hence, recovering full state information of the network is tantamount to estimating all the values of the tensor. Given measurements received from $\mu$phasor measurement units and/or smart meters, the recovery of unobserved quantities is carried out using the low-rank canonical polyadic decomposition of the state tensor---that is, the state estimation task is posed as a tensor imputation problem utilizing observed patterns in measured quantities. Two structured sampling schemes are considered: slab sampling and fiber sampling. For both schemes, we present sufficient conditions on the number of sampled slabs and fibers that guarantee identifiability of the factors of the state tensor. Numerical results demonstrate the ability of the proposed framework to achieve high estimation accuracy in multiple sampling scenarios.

Physics-Informed Deep Neural Network Method for Limited Observability State Estimation

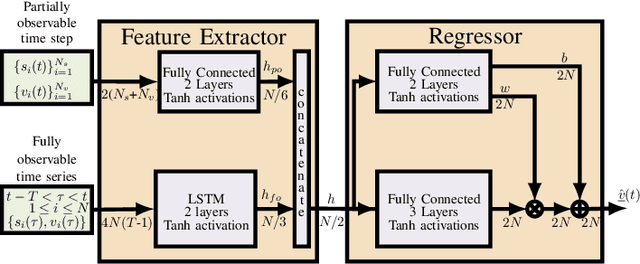
The precise knowledge regarding the state of the power grid is important in order to ensure optimal and reliable grid operation. Specifically, knowing the state of the distribution grid becomes increasingly important as more renewable energy sources are connected directly into the distribution network, increasing the fluctuations of the injected power. In this paper, we consider the case when the distribution grid becomes partially observable, and the state estimation problem is under-determined. We present a new methodology that leverages a deep neural network (DNN) to estimate the grid state. The standard DNN training method is modified to explicitly incorporate the physical information of the grid topology and line/shunt admittance. We show that our method leads to a superior accuracy of the estimation when compared to the case when no physical information is provided. Finally, we compare the performance of our method to the standard state estimation approach, which is based on the weighted least squares with pseudo-measurements, and show that our method performs significantly better with respect to the estimation accuracy.

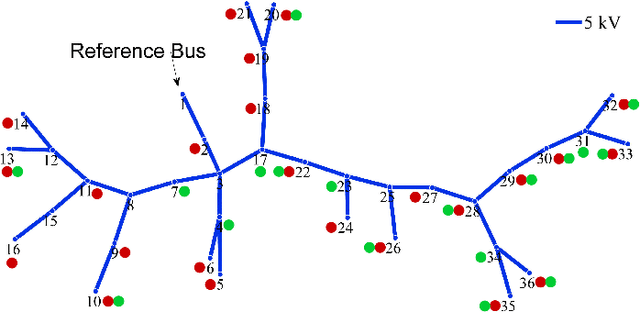
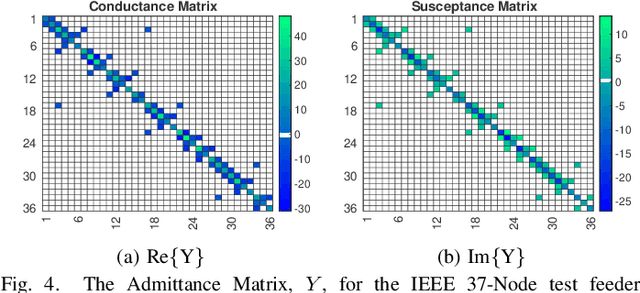
Robust Matrix Completion State Estimation in Distribution Systems

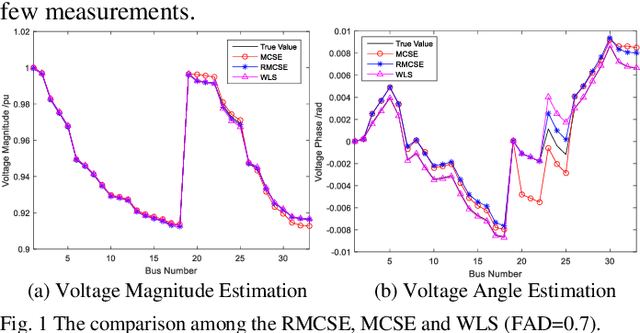
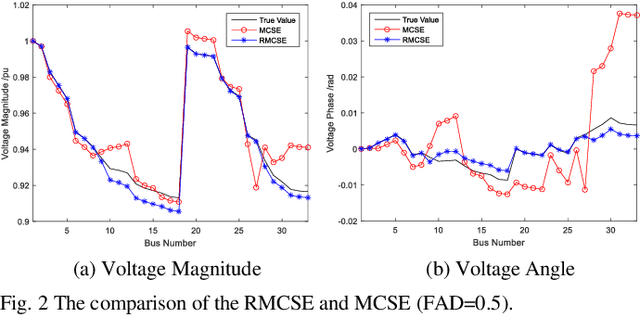
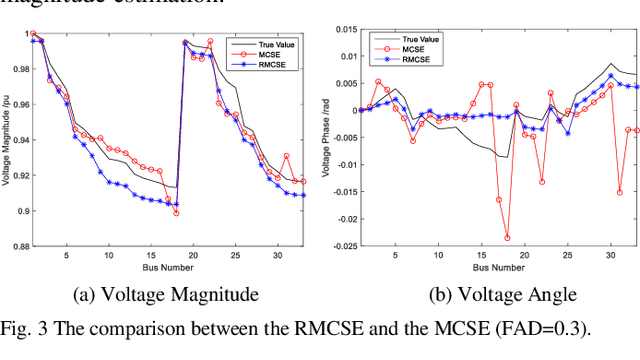
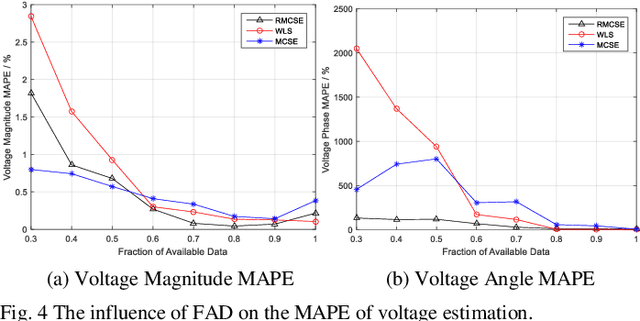
Due to the insufficient measurements in the distribution system state estimation (DSSE), full observability and redundant measurements are difficult to achieve without using the pseudo measurements. The matrix completion state estimation (MCSE) combines the matrix completion and power system model to estimate voltage by exploring the low-rank characteristics of the matrix. This paper proposes a robust matrix completion state estimation (RMCSE) to estimate the voltage in a distribution system under a low-observability condition. Tradition state estimation weighted least squares (WLS) method requires full observability to calculate the states and needs redundant measurements to proceed a bad data detection. The proposed method improves the robustness of the MCSE to bad data by minimizing the rank of the matrix and measurements residual with different weights. It can estimate the system state in a low-observability system and has robust estimates without the bad data detection process in the face of multiple bad data. The method is numerically evaluated on the IEEE 33-node radial distribution system. The estimation performance and robustness of RMCSE are compared with the WLS with the largest normalized residual bad data identification (WLS-LNR), and the MCSE.

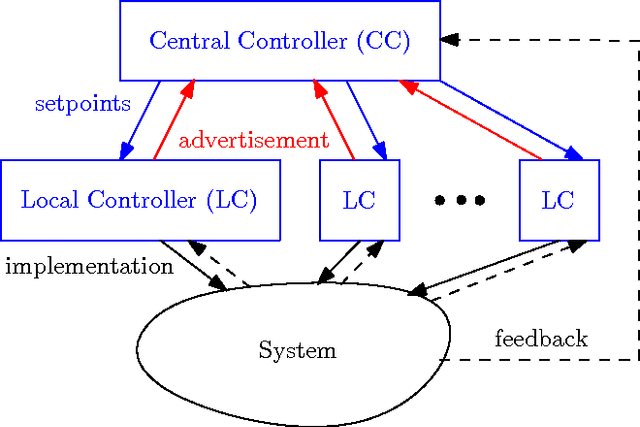
Bi-Level Online Control without Regret

This paper considers a bi-level discrete-time control framework with real-time constraints, consisting of several local controllers and a central controller. The objective is to bridge the gap between the online convex optimization and real-time control literature by proposing an online control algorithm with small dynamic regret, which is a natural performance criterion in nonstationary environments related to real-time control problems. We illustrate how the proposed algorithm can be applied to real-time control of power setpoints in an electrical grid.

Response-Based Approachability and its Application to Generalized No-Regret Algorithms

Approachability theory, introduced by Blackwell (1956), provides fundamental results on repeated games with vector-valued payoffs, and has been usefully applied since in the theory of learning in games and to learning algorithms in the online adversarial setup. Given a repeated game with vector payoffs, a target set $S$ is approachable by a certain player (the agent) if he can ensure that the average payoff vector converges to that set no matter what his adversary opponent does. Blackwell provided two equivalent sets of conditions for a convex set to be approachable. The first (primary) condition is a geometric separation condition, while the second (dual) condition requires that the set be {\em non-excludable}, namely that for every mixed action of the opponent there exists a mixed action of the agent (a {\em response}) such that the resulting payoff vector belongs to $S$. Existing approachability algorithms rely on the primal condition and essentially require to compute at each stage a projection direction from a given point to $S$. In this paper, we introduce an approachability algorithm that relies on Blackwell's {\em dual} condition. Thus, rather than projection, the algorithm relies on computation of the response to a certain action of the opponent at each stage. The utility of the proposed algorithm is demonstrated by applying it to certain generalizations of the classical regret minimization problem, which include regret minimization with side constraints and regret minimization for global cost functions. In these problems, computation of the required projections is generally complex but a response is readily obtainable.