Zero-shot Forecasting by Simulation Alone

Zero-shot time-series forecasting holds great promise, but is still in its infancy, hindered by limited and biased data corpora, leakage-prone evaluation, and privacy and licensing constraints. Motivated by these challenges, we propose the first practical univariate time series simulation pipeline which is simultaneously fast enough for on-the-fly data generation and enables notable zero-shot forecasting performance on M-Series and GiftEval benchmarks that capture trend/seasonality/intermittency patterns, typical of industrial forecasting applications across a variety of domains. Our simulator, which we call SarSim0 (SARIMA Simulator for Zero-Shot Forecasting), is based off of a seasonal autoregressive integrated moving average (SARIMA) model as its core data source. Due to instability in the autoregressive component, naive SARIMA simulation often leads to unusable paths. Instead, we follow a three-step procedure: (1) we sample well-behaved trajectories from its characteristic polynomial stability region; (2) we introduce a superposition scheme that combines multiple paths into rich multi-seasonality traces; and (3) we add rate-based heavy-tailed noise models to capture burstiness and intermittency alongside seasonalities and trends. SarSim0 is orders of magnitude faster than kernel-based generators, and it enables training on circa 1B unique purely simulated series, generated on the fly; after which well-established neural network backbones exhibit strong zero-shot generalization, surpassing strong statistical forecasters and recent foundation baselines, while operating under strict zero-shot protocol. Notably, on GiftEval we observe a "student-beats-teacher" effect: models trained on our simulations exceed the forecasting accuracy of the AutoARIMA generating processes.

Bayesian Nonparametric Kernel-Learning

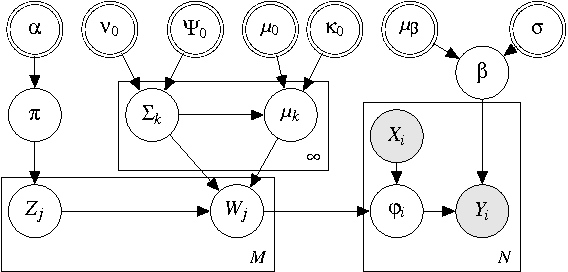
Kernel methods are ubiquitous tools in machine learning. However, there is often little reason for the common practice of selecting a kernel a priori. Even if a universal approximating kernel is selected, the quality of the finite sample estimator may be greatly affected by the choice of kernel. Furthermore, when directly applying kernel methods, one typically needs to compute a $N \times N$ Gram matrix of pairwise kernel evaluations to work with a dataset of $N$ instances. The computation of this Gram matrix precludes the direct application of kernel methods on large datasets, and makes kernel learning especially difficult. In this paper we introduce Bayesian nonparmetric kernel-learning (BaNK), a generic, data-driven framework for scalable learning of kernels. BaNK places a nonparametric prior on the spectral distribution of random frequencies allowing it to both learn kernels and scale to large datasets. We show that this framework can be used for large scale regression and classification tasks. Furthermore, we show that BaNK outperforms several other scalable approaches for kernel learning on a variety of real world datasets.