Distributed Adaptive Learning Under Communication Constraints

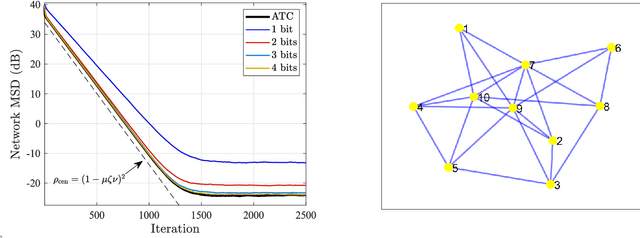
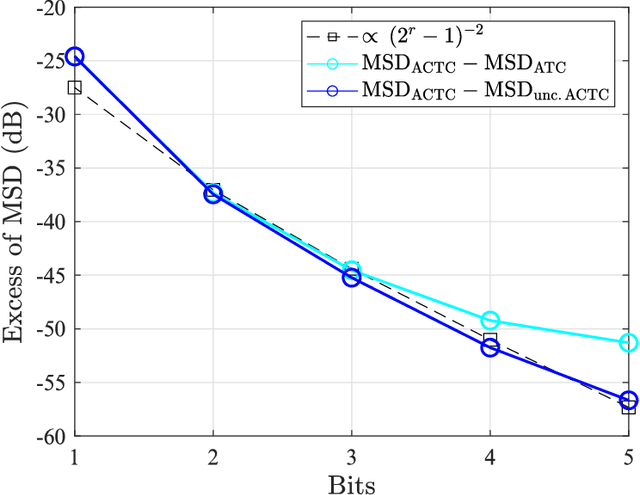
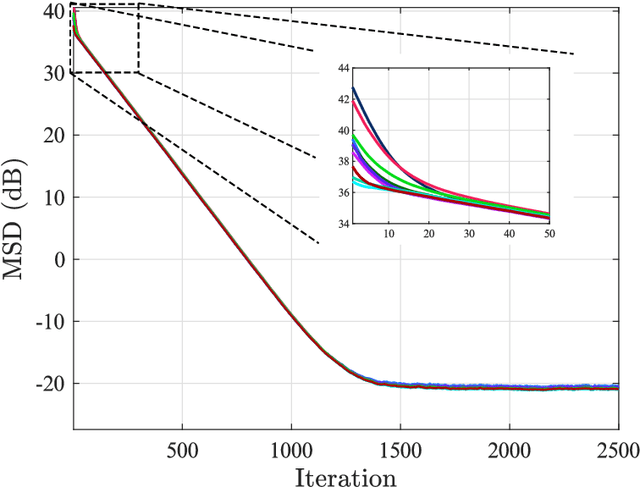
This work examines adaptive distributed learning strategies designed to operate under communication constraints. We consider a network of agents that must solve an online optimization problem from continual observation of streaming data. The agents implement a distributed cooperative strategy where each agent is allowed to perform local exchange of information with its neighbors. In order to cope with communication constraints, the exchanged information must be unavoidably compressed. We propose a diffusion strategy nicknamed as ACTC (Adapt-Compress-Then-Combine), which relies on the following steps: i) an adaptation step where each agent performs an individual stochastic-gradient update with constant step-size; ii) a compression step that leverages a recently introduced class of stochastic compression operators; and iii) a combination step where each agent combines the compressed updates received from its neighbors. The distinguishing elements of this work are as follows. First, we focus on adaptive strategies, where constant (as opposed to diminishing) step-sizes are critical to respond in real time to nonstationary variations. Second, we consider the general class of directed graphs and left-stochastic combination policies, which allow us to enhance the interplay between topology and learning. Third, in contrast with related works that assume strong convexity for all individual agents' cost functions, we require strong convexity only at a network level, a condition satisfied even if a single agent has a strongly-convex cost and the remaining agents have non-convex costs. Fourth, we focus on a diffusion (as opposed to consensus) strategy. Under the demanding setting of compressed information, we establish that the ACTC iterates fluctuate around the desired optimizer, achieving remarkable savings in terms of bits exchanged between neighboring agents.

Hidden Markov Modeling over Graphs

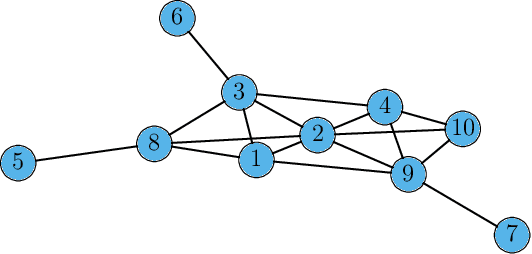
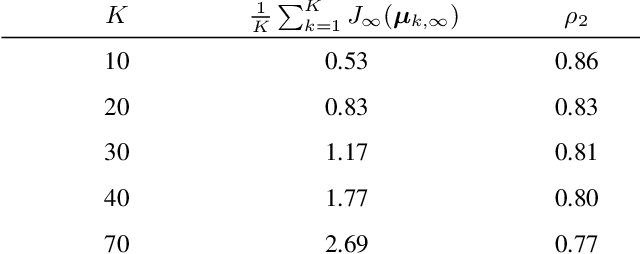
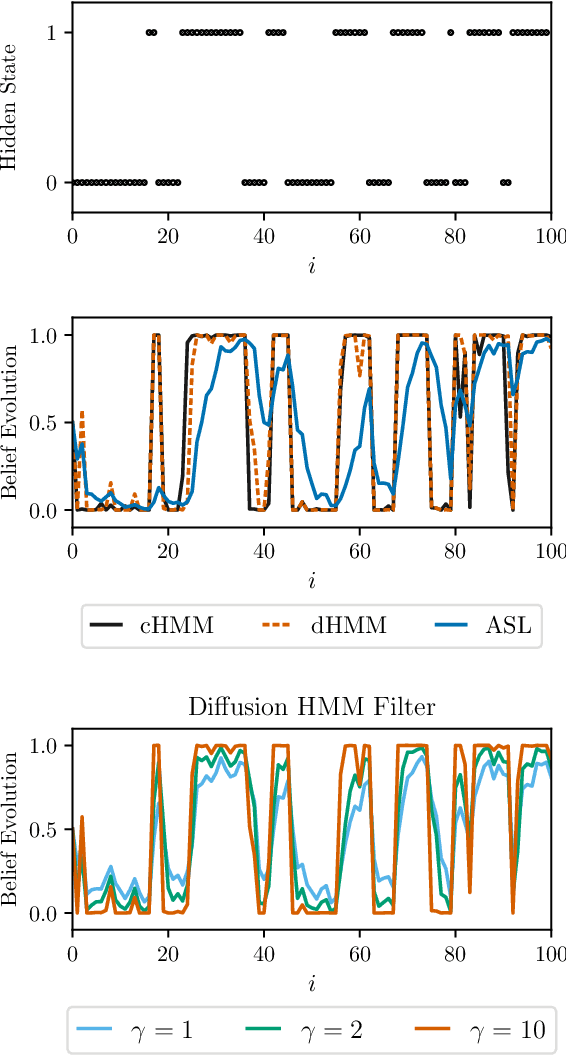
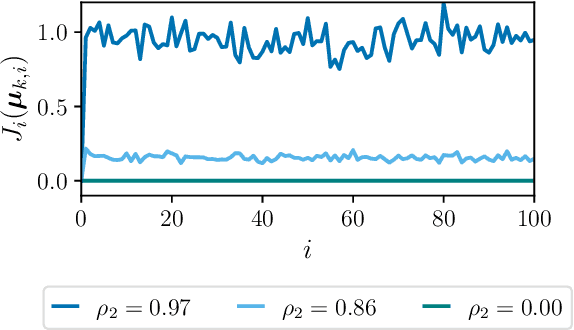
This work proposes a multi-agent filtering algorithm over graphs for finite-state hidden Markov models (HMMs), which can be used for sequential state estimation or for tracking opinion formation over dynamic social networks. We show that the difference from the optimal centralized Bayesian solution is asymptotically bounded for geometrically ergodic transition models. Experiments illustrate the theoretical findings and in particular, demonstrate the superior performance of the proposed algorithm compared to a state-of-the-art social learning algorithm.

A Graph Federated Architecture with Privacy Preserving Learning

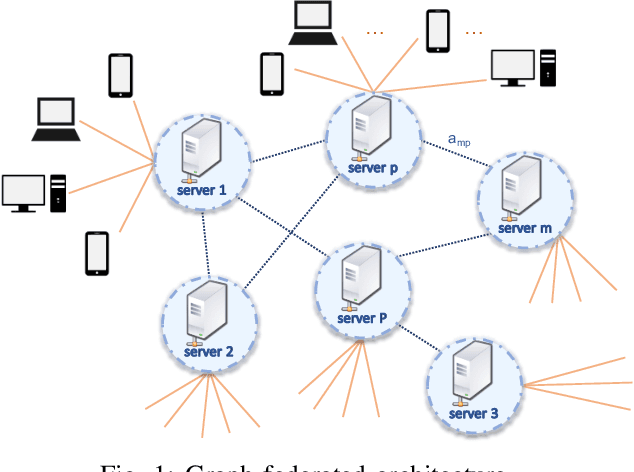
Federated learning involves a central processor that works with multiple agents to find a global model. The process consists of repeatedly exchanging estimates, which results in the diffusion of information pertaining to the local private data. Such a scheme can be inconvenient when dealing with sensitive data, and therefore, there is a need for the privatization of the algorithms. Furthermore, the current architecture of a server connected to multiple clients is highly sensitive to communication failures and computational overloads at the server. Thus in this work, we develop a private multi-server federated learning scheme, which we call graph federated learning. We use cryptographic and differential privacy concepts to privatize the federated learning algorithm that we extend to the graph structure. We study the effect of privatization on the performance of the learning algorithm for general private schemes that can be modeled as additive noise. We show under convexity and Lipschitz conditions, that the privatized process matches the performance of the non-private algorithm, even when we increase the noise variance.

Competing Adaptive Networks

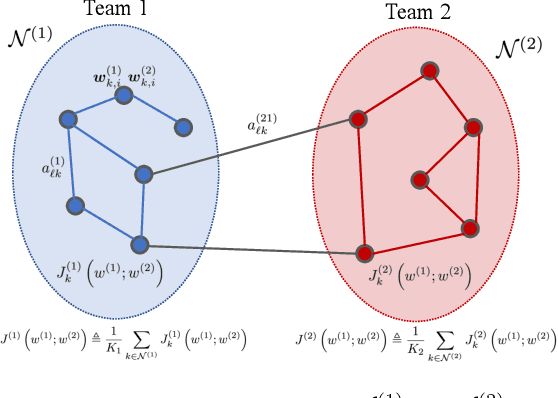
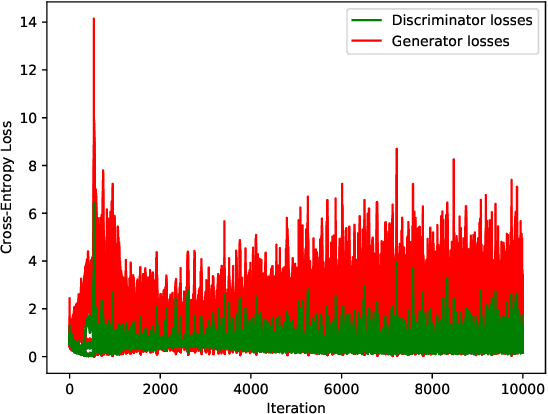
Adaptive networks have the capability to pursue solutions of global stochastic optimization problems by relying only on local interactions within neighborhoods. The diffusion of information through repeated interactions allows for globally optimal behavior, without the need for central coordination. Most existing strategies are developed for cooperative learning settings, where the objective of the network is common to all agents. We consider in this work a team setting, where a subset of the agents form a team with a common goal while competing with the remainder of the network. We develop an algorithm for decentralized competition among teams of adaptive agents, analyze its dynamics and present an application in the decentralized training of generative adversarial neural networks.

Decision-Making Algorithms for Learning and Adaptation with Application to COVID-19 Data

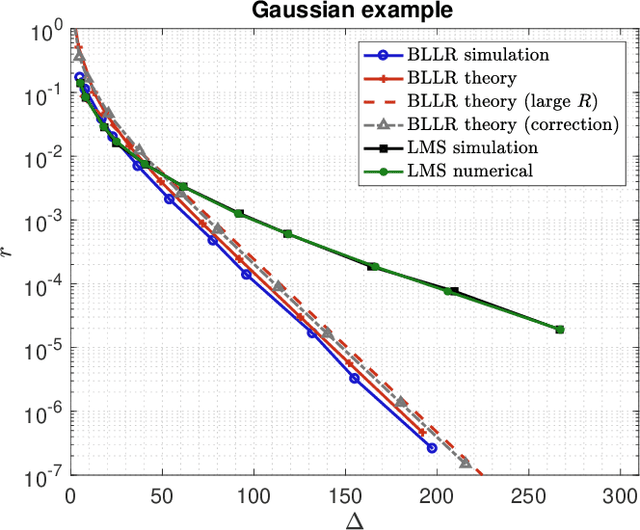
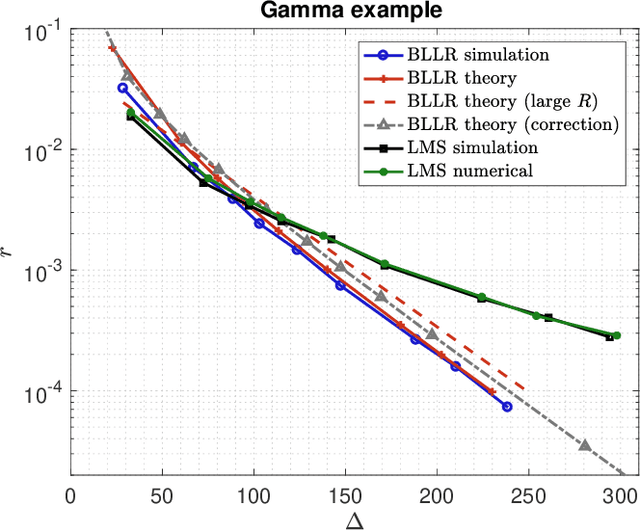
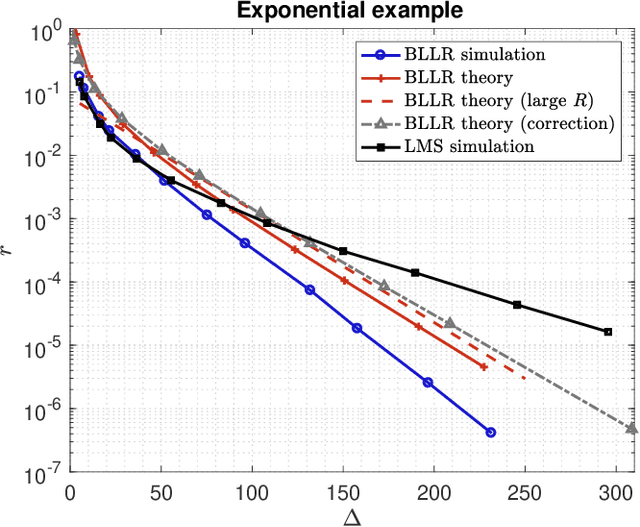
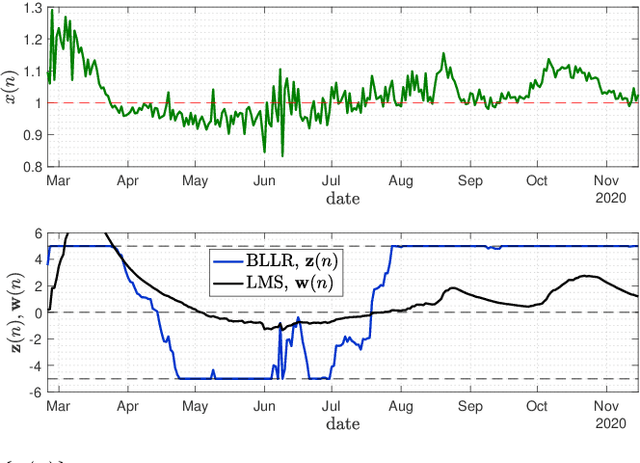
This work focuses on the development of a new family of decision-making algorithms for adaptation and learning, which are specifically tailored to decision problems and are constructed by building up on first principles from decision theory. A key observation is that estimation and decision problems are structurally different and, therefore, algorithms that have proven successful for the former need not perform well when adjusted for decision problems. We propose a new scheme, referred to as BLLR (barrier log-likelihood ratio algorithm) and demonstrate its applicability to real-data from the COVID-19 pandemic in Italy. The results illustrate the ability of the design tool to track the different phases of the outbreak.

Federated Learning under Importance Sampling

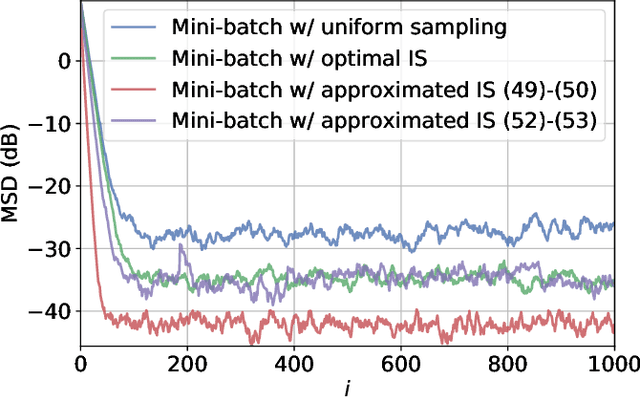
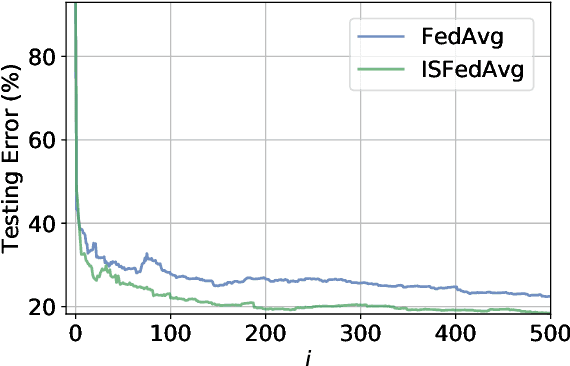
Federated learning encapsulates distributed learning strategies that are managed by a central unit. Since it relies on using a selected number of agents at each iteration, and since each agent, in turn, taps into its local data, it is only natural to study optimal sampling policies for selecting agents and their data in federated learning implementations. Usually, only uniform sampling schemes are used. However, in this work, we examine the effect of importance sampling and devise schemes for sampling agents and data non-uniformly guided by a performance measure. We find that in schemes involving sampling without replacement, the performance of the resulting architecture is controlled by two factors related to data variability at each agent, and model variability across agents. We illustrate the theoretical findings with experiments on simulated and real data and show the improvement in performance that results from the proposed strategies.

Second-Order Guarantees in Federated Learning

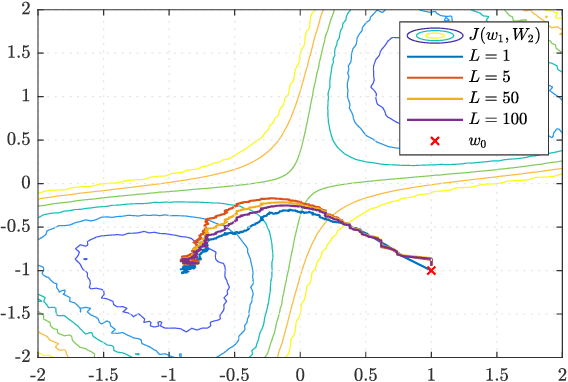
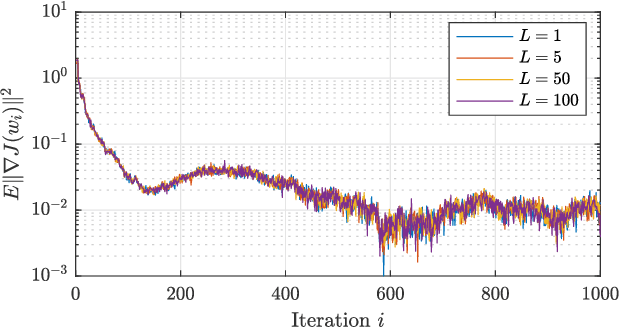
Federated learning is a useful framework for centralized learning from distributed data under practical considerations of heterogeneity, asynchrony, and privacy. Federated architectures are frequently deployed in deep learning settings, which generally give rise to non-convex optimization problems. Nevertheless, most existing analysis are either limited to convex loss functions, or only establish first-order stationarity, despite the fact that saddle-points, which are first-order stationary, are known to pose bottlenecks in deep learning. We draw on recent results on the second-order optimality of stochastic gradient algorithms in centralized and decentralized settings, and establish second-order guarantees for a class of federated learning algorithms.

Optimal Importance Sampling for Federated Learning

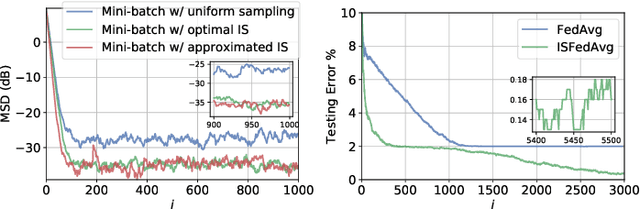
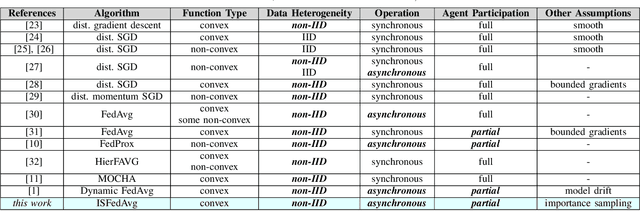
Federated learning involves a mixture of centralized and decentralized processing tasks, where a server regularly selects a sample of the agents and these in turn sample their local data to compute stochastic gradients for their learning updates. This process runs continually. The sampling of both agents and data is generally uniform; however, in this work we consider non-uniform sampling. We derive optimal importance sampling strategies for both agent and data selection and show that non-uniform sampling without replacement improves the performance of the original FedAvg algorithm. We run experiments on a regression and classification problem to illustrate the theoretical results.

Network Classifiers Based on Social Learning

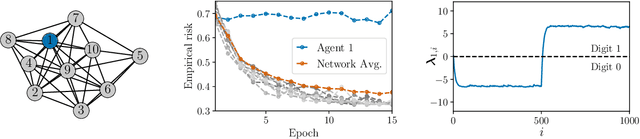
This work proposes a new way of combining independently trained classifiers over space and time. Combination over space means that the outputs of spatially distributed classifiers are aggregated. Combination over time means that the classifiers respond to streaming data during testing and continue to improve their performance even during this phase. By doing so, the proposed architecture is able to improve prediction performance over time with unlabeled data. Inspired by social learning algorithms, which require prior knowledge of the observations distribution, we propose a Social Machine Learning (SML) paradigm that is able to exploit the imperfect models generated during the learning phase. We show that this strategy results in consistent learning with high probability, and it yields a robust structure against poorly trained classifiers. Simulations with an ensemble of feedforward neural networks are provided to illustrate the theoretical results.

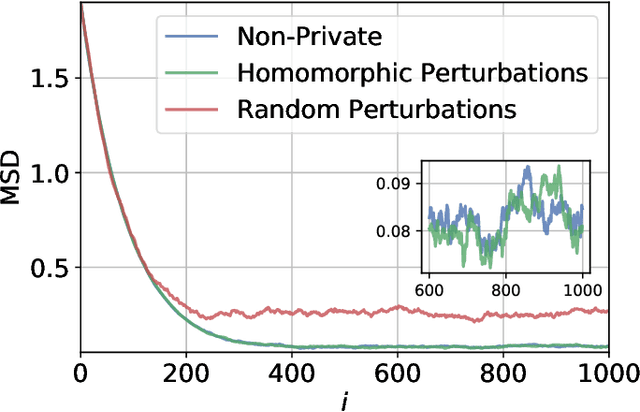
Graph-Homomorphic Perturbations for Private Decentralized Learning

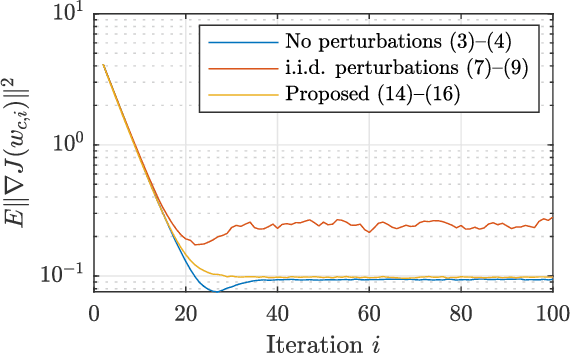
Decentralized algorithms for stochastic optimization and learning rely on the diffusion of information as a result of repeated local exchanges of intermediate estimates. Such structures are particularly appealing in situations where agents may be hesitant to share raw data due to privacy concerns. Nevertheless, in the absence of additional privacy-preserving mechanisms, the exchange of local estimates, which are generated based on private data can allow for the inference of the data itself. The most common mechanism for guaranteeing privacy is the addition of perturbations to local estimates before broadcasting. These perturbations are generally chosen independently at every agent, resulting in a significant performance loss. We propose an alternative scheme, which constructs perturbations according to a particular nullspace condition, allowing them to be invisible (to first order in the step-size) to the network centroid, while preserving privacy guarantees. The analysis allows for general nonconvex loss functions, and is hence applicable to a large number of machine learning and signal processing problems, including deep learning.