Statistical Hypothesis Testing Based on Machine Learning: Large Deviations Analysis

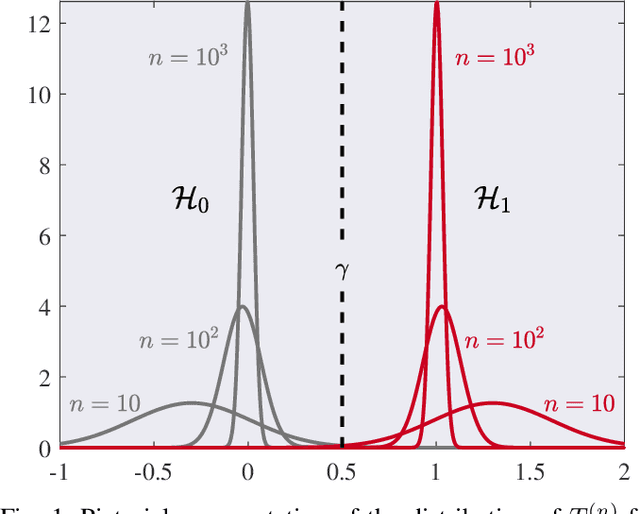
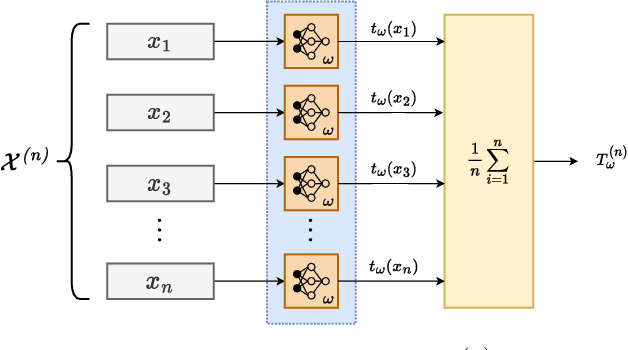
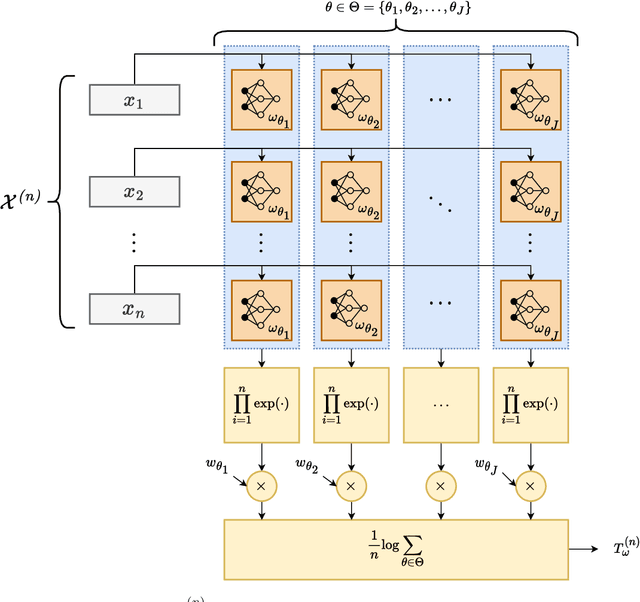
We study the performance -- and specifically the rate at which the error probability converges to zero -- of Machine Learning (ML) classification techniques. Leveraging the theory of large deviations, we provide the mathematical conditions for a ML classifier to exhibit error probabilities that vanish exponentially, say $\sim \exp\left(-n\,I + o(n) \right)$, where $n$ is the number of informative observations available for testing (or another relevant parameter, such as the size of the target in an image) and $I$ is the error rate. Such conditions depend on the Fenchel-Legendre transform of the cumulant-generating function of the Data-Driven Decision Function (D3F, i.e., what is thresholded before the final binary decision is made) learned in the training phase. As such, the D3F and, consequently, the related error rate $I$, depend on the given training set, which is assumed of finite size. Interestingly, these conditions can be verified and tested numerically exploiting the available dataset, or a synthetic dataset, generated according to the available information on the underlying statistical model. In other words, the classification error probability convergence to zero and its rate can be computed on a portion of the dataset available for training. Coherently with the large deviations theory, we can also establish the convergence, for $n$ large enough, of the normalized D3F statistic to a Gaussian distribution. This property is exploited to set a desired asymptotic false alarm probability, which empirically turns out to be accurate even for quite realistic values of $n$. Furthermore, approximate error probability curves $\sim \zeta_n \exp\left(-n\,I \right)$ are provided, thanks to the refined asymptotic derivation (often referred to as exact asymptotics), where $\zeta_n$ represents the most representative sub-exponential terms of the error probabilities.

Structured Covariance Matrix Estimation with Missing-Data for Radar Applications via Expectation-Maximization

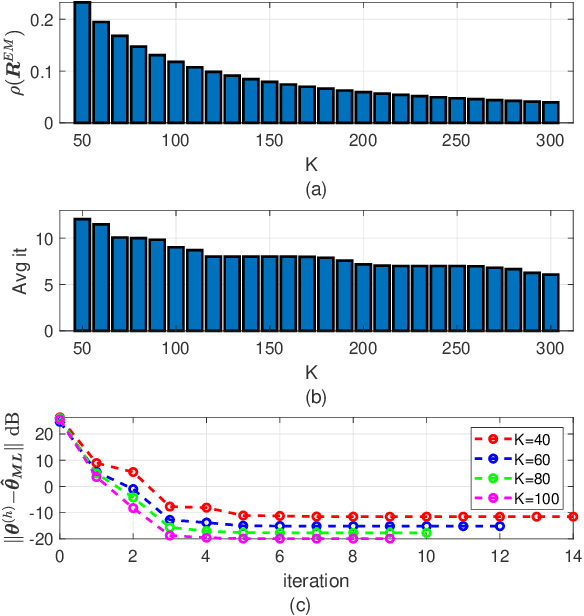
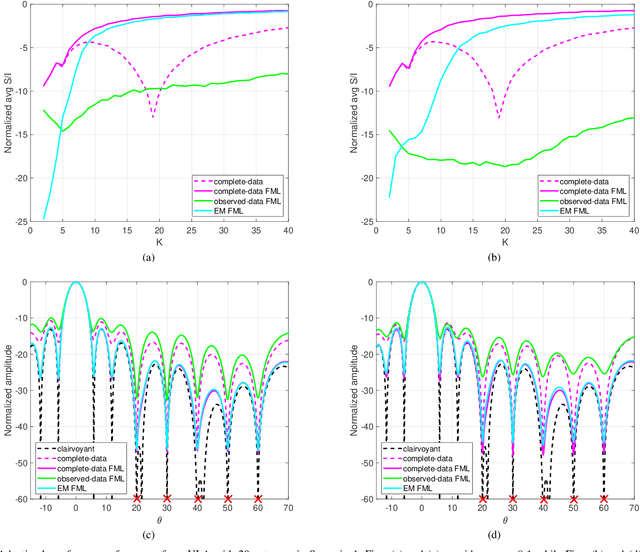
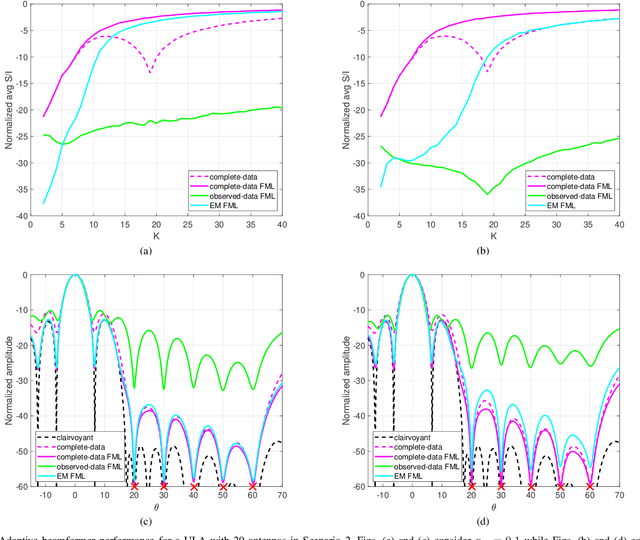
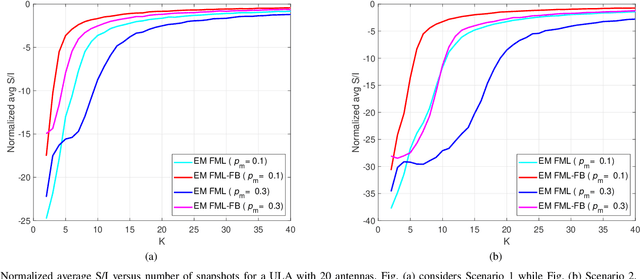
Structured covariance matrix estimation in the presence of missing data is addressed in this paper with emphasis on radar signal processing applications. After a motivation of the study, the array model is specified and the problem of computing the maximum likelihood estimate of a structured covariance matrix is formulated. A general procedure to optimize the observed-data likelihood function is developed resorting to the expectation-maximization algorithm. The corresponding convergence properties are thoroughly established and the rate of convergence is analyzed. The estimation technique is contextualized for two practically relevant radar problems: beamforming and detection of the number of sources. In the former case an adaptive beamformer leveraging the EM-based estimator is presented; in the latter, detection techniques generalizing the classic Akaike information criterion, minimum description length, and Hannan-Quinn information criterion, are introduced. Numerical results are finally presented to corroborate the theoretical study.

Quickest Detection and Forecast of Pandemic Outbreaks: Analysis of COVID-19 Waves

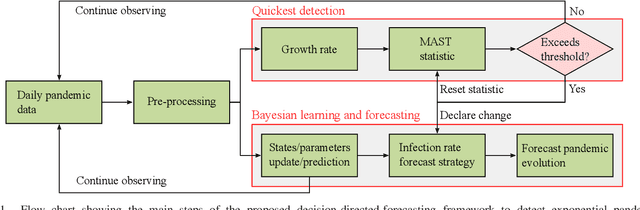
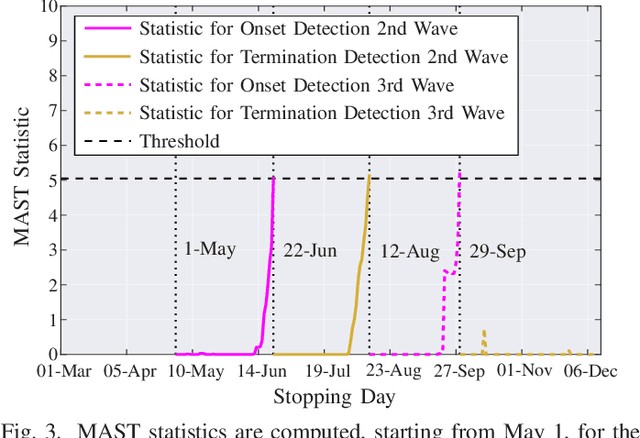
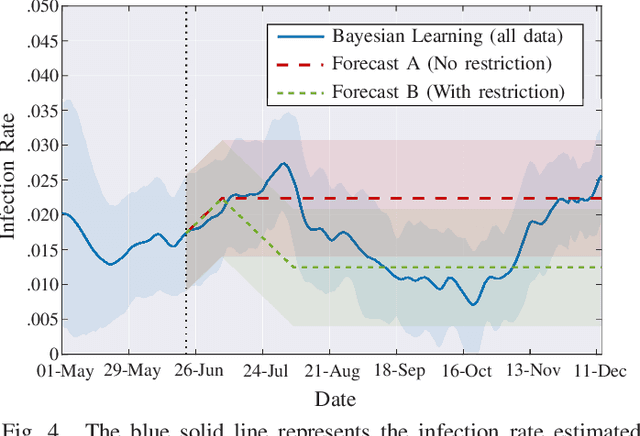
The COVID-19 pandemic has, worldwide and up to December 2020, caused over 1.7 million deaths, and put the world's most advanced healthcare systems under heavy stress. In many countries, drastic restriction measures adopted by political authorities, such as national lockdowns, have not prevented the outbreak of new pandemic's waves. In this article, we propose an integrated detection-estimation-forecasting framework that, using publicly available data published by the national authorities, is designed to: (i) learn relevant features of the epidemic (e.g., the infection rate); (ii) detect as quickly as possible the onset (or the termination) of an exponential growth of the contagion; and (iii) reliably forecast the epidemic evolution. The proposed solution is validated by analyzing the COVID-19 second and third waves in the USA.

Decision-Making Algorithms for Learning and Adaptation with Application to COVID-19 Data

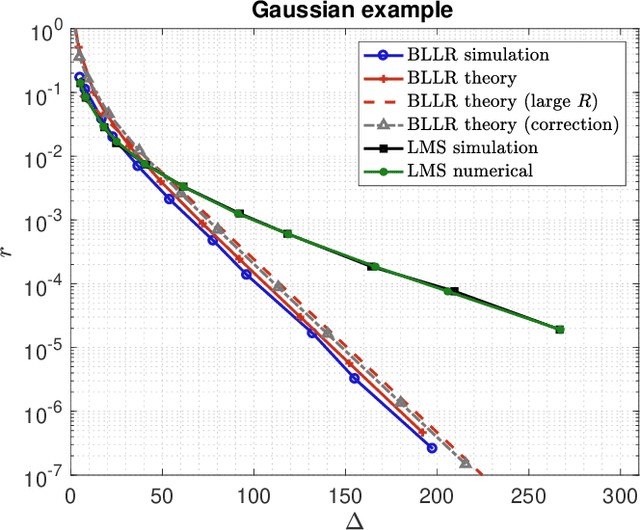
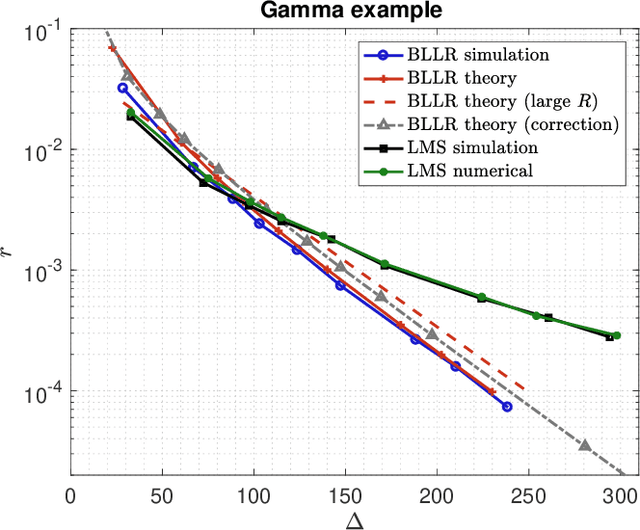
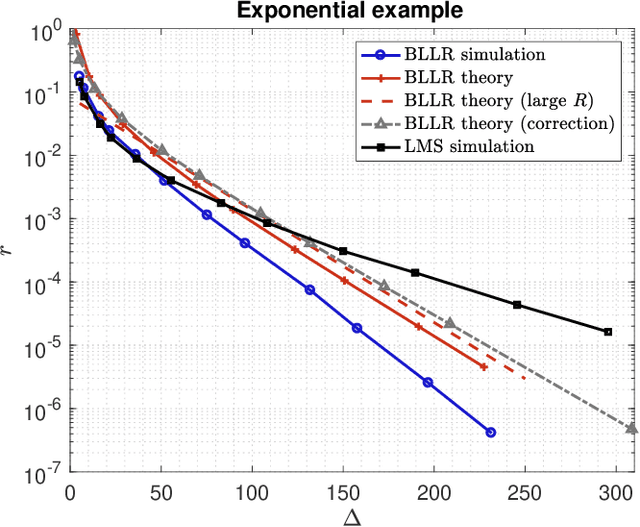
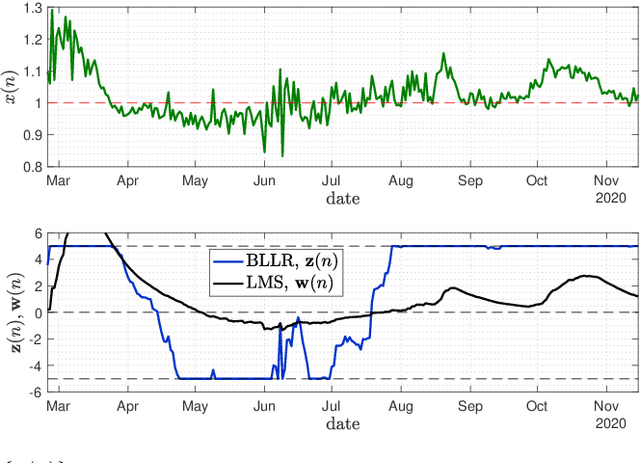
This work focuses on the development of a new family of decision-making algorithms for adaptation and learning, which are specifically tailored to decision problems and are constructed by building up on first principles from decision theory. A key observation is that estimation and decision problems are structurally different and, therefore, algorithms that have proven successful for the former need not perform well when adjusted for decision problems. We propose a new scheme, referred to as BLLR (barrier log-likelihood ratio algorithm) and demonstrate its applicability to real-data from the COVID-19 pandemic in Italy. The results illustrate the ability of the design tool to track the different phases of the outbreak.

Distributed Chernoff Test: Optimal decision systems over networks

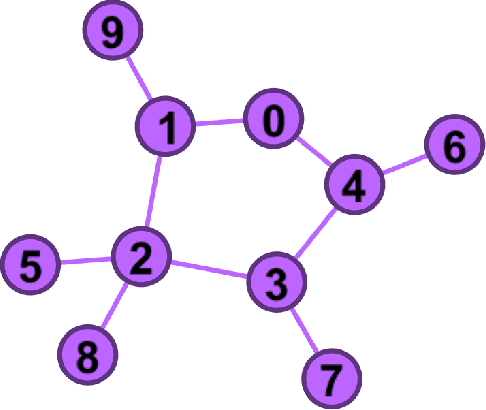
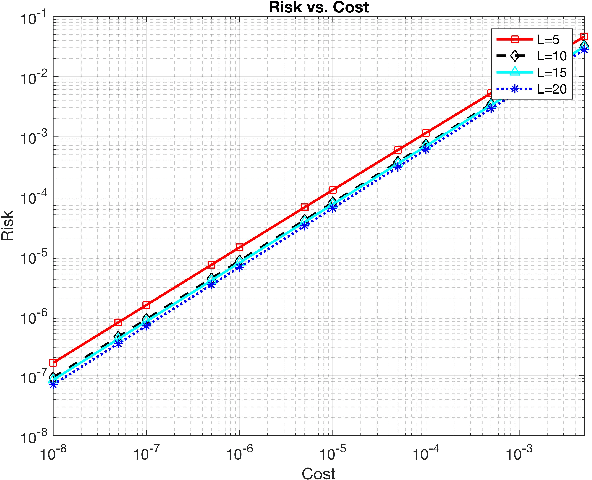
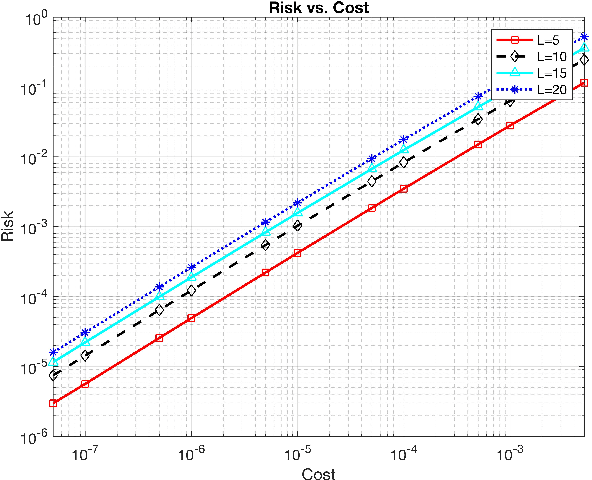
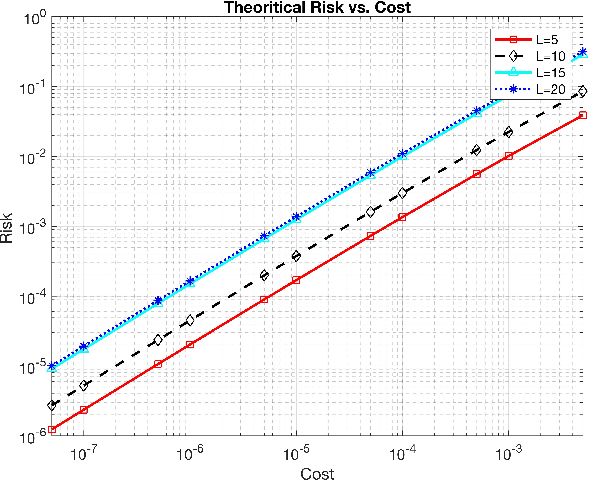
In this work, we propose two different sequential and adaptive hypothesis tests, motivated from classic Chernoff's test, for both decentralized and distributed setup of sensor networks. In the former setup, the sensors can communicate via central entity i.e. fusion center. On the other hand, in the latter setup, sensors are connected via communication link, and no central entity is present to facilitate the communication. We compare the performance of these tests with the optimal consistent sequential test in the sensor network. In decentralized setup, the proposed test achieves the same asymptotic optimality of the classic one, minimizing the expected cost required to reach a decision plus the expected cost of making a wrong decision, when the observation cost per unit time tends to zero. This test is also asymptotic optimal in the higher moments of decision time. The proposed test is parsimonious in terms of communications as the expected number of channel uses required by each sensor, in the regime of vanishing observation cost per unit time, to complete the test converges to four.In distributed setup, the proposed test is evaluated on the same performance measures as the test in decentralized setup. We also provide sufficient conditions for which the proposed test in distributed setup also achieves the same asymptotic optimality as the classic one. Like the proposed test in decentralized setup, under these sufficient conditions, the proposed test in distributed setup is also asymptotic optimal in the higher moments of time required to reach a decision in the sensor network. This test is parsimonious is terms of communications in comparison to the state of art schemes proposed in the literature for distributed hypothesis testing.