Optimizing Deep Learning Recommender Systems' Training On CPU Cluster Architectures

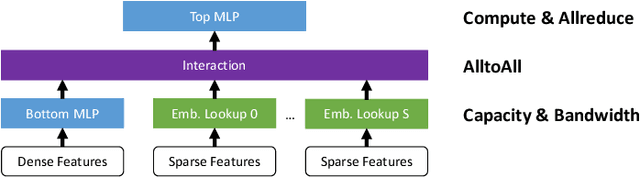
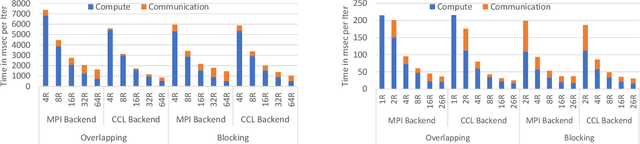
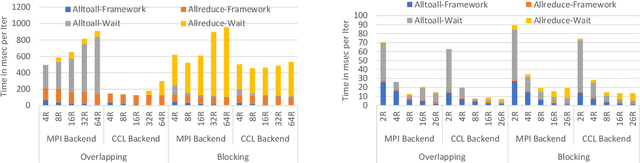
During the last two years, the goal of many researchers has been to squeeze the last bit of performance out of HPC system for AI tasks. Often this discussion is held in the context of how fast ResNet50 can be trained. Unfortunately, ResNet50 is no longer a representative workload in 2020. Thus, we focus on Recommender Systems which account for most of the AI cycles in cloud computing centers. More specifically, we focus on Facebook's DLRM benchmark. By enabling it to run on latest CPU hardware and software tailored for HPC, we are able to achieve more than two-orders of magnitude improvement in performance (110x) on a single socket compared to the reference CPU implementation, and high scaling efficiency up to 64 sockets, while fitting ultra-large datasets. This paper discusses the optimization techniques for the various operators in DLRM and which component of the systems are stressed by these different operators. The presented techniques are applicable to a broader set of DL workloads that pose the same scaling challenges/characteristics as DLRM.

PolyScientist: Automatic Loop Transformations Combined with Microkernels for Optimization of Deep Learning Primitives

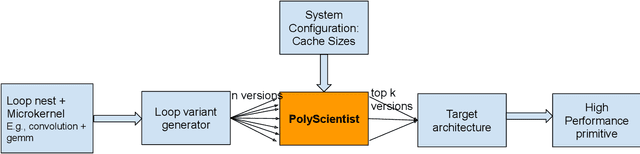
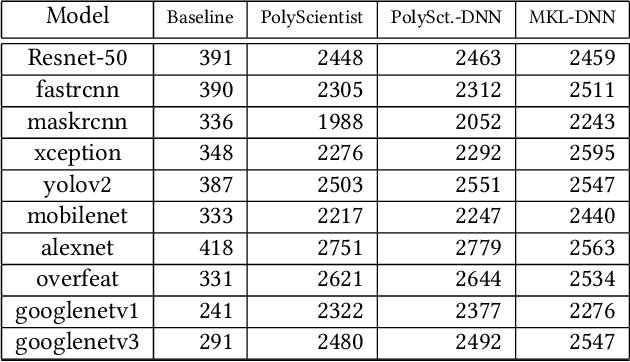
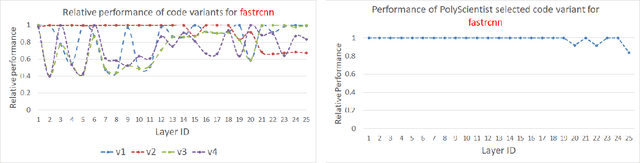
At the heart of deep learning training and inferencing are computationally intensive primitives such as convolutions which form the building blocks of deep neural networks. Researchers have taken two distinct approaches to creating high performance implementations of deep learning kernels, namely, 1) library development exemplified by Intel MKL-DNN for CPUs, 2) automatic compilation represented by the TensorFlow XLA compiler. The two approaches have their drawbacks: even though a custom built library can deliver very good performance, the cost and time of development of the library can be high. Automatic compilation of kernels is attractive but in practice, till date, automatically generated implementations lag expert coded kernels in performance by orders of magnitude. In this paper, we develop a hybrid solution to the development of deep learning kernels that achieves the best of both worlds: the expert coded microkernels are utilized for the innermost loops of kernels and we use the advanced polyhedral technology to automatically tune the outer loops for performance. We design a novel polyhedral model based data reuse algorithm to optimize the outer loops of the kernel. Through experimental evaluation on an important class of deep learning primitives namely convolutions, we demonstrate that the approach we develop attains the same levels of performance as Intel MKL-DNN, a hand coded deep learning library.

Training Neural Machine Translation (NMT) Models using Tensor Train Decomposition on TensorFlow (T3F)

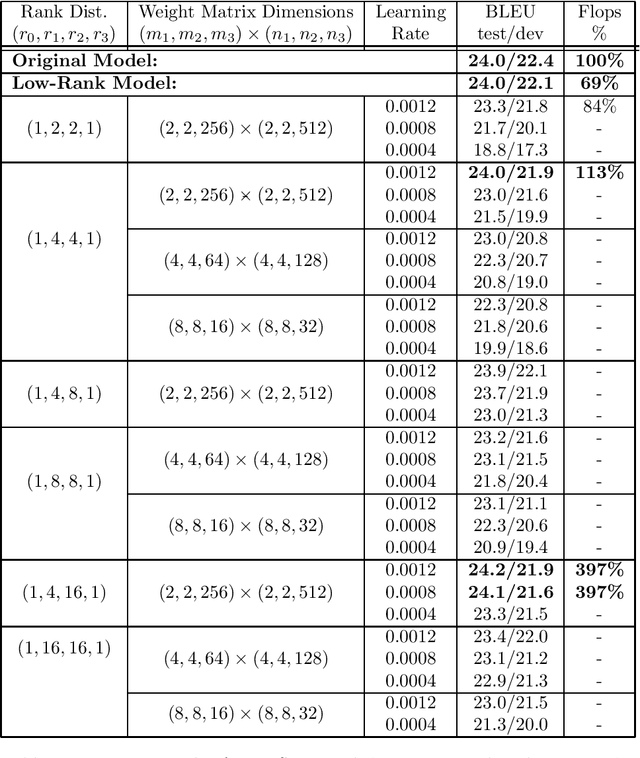
We implement a Tensor Train layer in the TensorFlow Neural Machine Translation (NMT) model using the t3f library. We perform training runs on the IWSLT English-Vietnamese '15 and WMT German-English '16 datasets with learning rates $\in \{0.0004,0.0008,0.0012\}$, maximum ranks $\in \{2,4,8,16\}$ and a range of core dimensions. We compare against a target BLEU test score of 24.0, obtained by our benchmark run. For the IWSLT English-Vietnamese training, we obtain BLEU test/dev scores of 24.0/21.9 and 24.2/21.9 using core dimensions $(2, 2, 256) \times (2, 2, 512)$ with learning rate 0.0012 and rank distributions $(1,4,4,1)$ and $(1,4,16,1)$ respectively. These runs use 113\% and 397\% of the flops of the benchmark run respectively. We find that, of the parameters surveyed, a higher learning rate and more `rectangular' core dimensions generally produce higher BLEU scores. For the WMT German-English dataset, we obtain BLEU scores of 24.0/23.8 using core dimensions $(4, 4, 128) \times (4, 4, 256)$ with learning rate 0.0012 and rank distribution $(1,2,2,1)$. We discuss the potential for future optimization and application of Tensor Train decomposition to other NMT models.

High-Performance Deep Learning via a Single Building Block

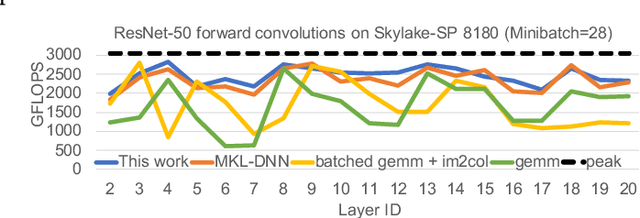
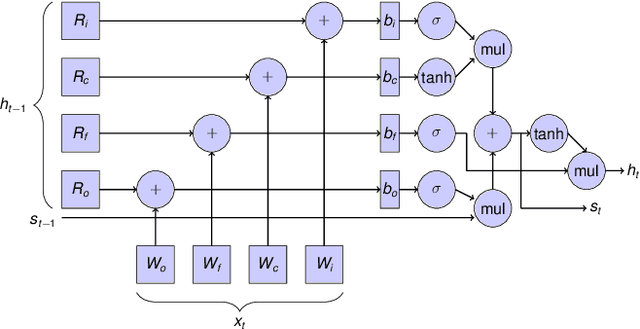
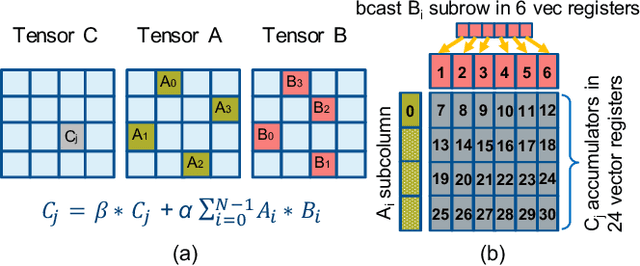
Deep learning (DL) is one of the most prominent branches of machine learning. Due to the immense computational cost of DL workloads, industry and academia have developed DL libraries with highly-specialized kernels for each workload/architecture, leading to numerous, complex code-bases that strive for performance, yet they are hard to maintain and do not generalize. In this work, we introduce the batch-reduce GEMM kernel and show how the most popular DL algorithms can be formulated with this kernel as the basic building-block. Consequently, the DL library-development degenerates to mere (potentially automatic) tuning of loops around this sole optimized kernel. By exploiting our new kernel we implement Recurrent Neural Networks, Convolution Neural Networks and Multilayer Perceptron training and inference primitives in just 3K lines of high-level code. Our primitives outperform vendor-optimized libraries on multi-node CPU clusters, and we also provide proof-of-concept CNN kernels targeting GPUs. Finally, we demonstrate that the batch-reduce GEMM kernel within a tensor compiler yields high-performance CNN primitives, further amplifying the viability of our approach.

A Study of BFLOAT16 for Deep Learning Training

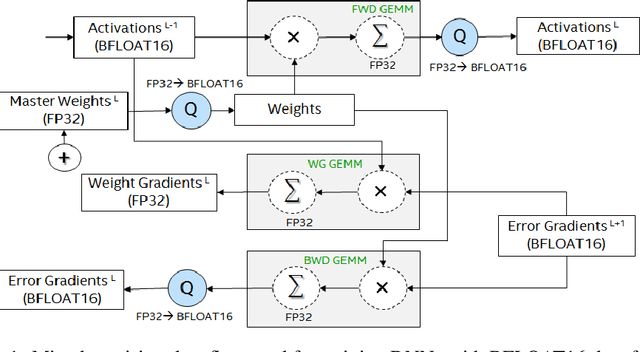
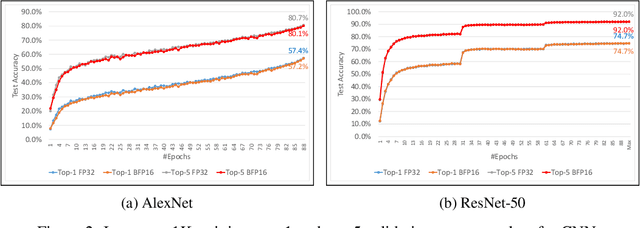
This paper presents the first comprehensive empirical study demonstrating the efficacy of the Brain Floating Point (BFLOAT16) half-precision format for Deep Learning training across image classification, speech recognition, language modeling, generative networks and industrial recommendation systems. BFLOAT16 is attractive for Deep Learning training for two reasons: the range of values it can represent is the same as that of IEEE 754 floating-point format (FP32) and conversion to/from FP32 is simple. Maintaining the same range as FP32 is important to ensure that no hyper-parameter tuning is required for convergence; e.g., IEEE 754 compliant half-precision floating point (FP16) requires hyper-parameter tuning. In this paper, we discuss the flow of tensors and various key operations in mixed precision training, and delve into details of operations, such as the rounding modes for converting FP32 tensors to BFLOAT16. We have implemented a method to emulate BFLOAT16 operations in Tensorflow, Caffe2, IntelCaffe, and Neon for our experiments. Our results show that deep learning training using BFLOAT16 tensors achieves the same state-of-the-art (SOTA) results across domains as FP32 tensors in the same number of iterations and with no changes to hyper-parameters.

ISA Mapper: A Compute and Hardware Agnostic Deep Learning Compiler

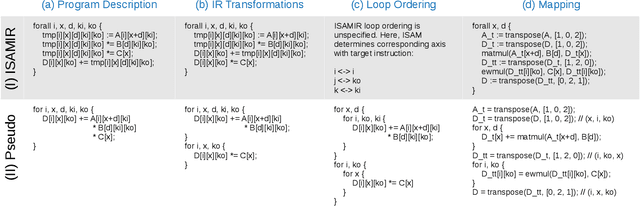
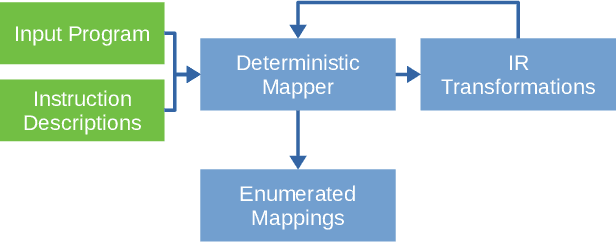
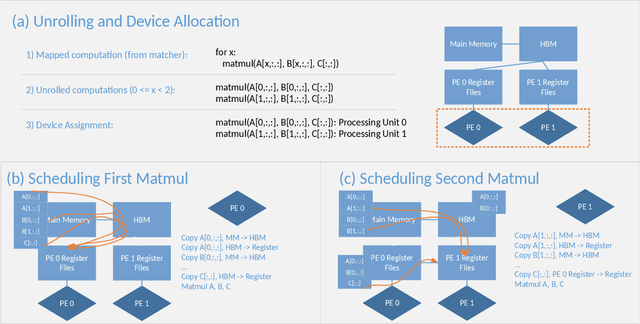
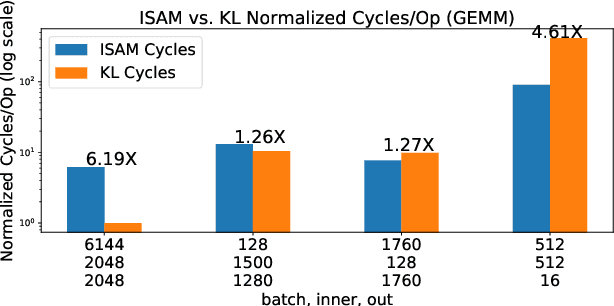
Domain specific accelerators present new challenges and opportunities for code generation onto novel instruction sets, communication fabrics, and memory architectures. In this paper we introduce an intermediate representation (IR) which enables both deep learning computational kernels and hardware capabilities to be described in the same IR. We then formulate and apply instruction mapping to determine the possible ways a computation can be performed on a hardware system. Next, our scheduler chooses a specific mapping and determines the data movement and computation order. In order to manage the large search space of mappings and schedules, we developed a flexible framework that allows heuristics, cost models, and potentially machine learning to facilitate this search problem. With this system, we demonstrate the automated extraction of matrix multiplication kernels out of recent deep learning kernels such as depthwise-separable convolution. In addition, we demonstrate two to five times better performance on DeepBench sized GEMMs and GRU RNN execution when compared to state-of-the-art (SOTA) implementations on new hardware and up to 85% of the performance for SOTA implementations on existing hardware.

Mixed Precision Training of Convolutional Neural Networks using Integer Operations

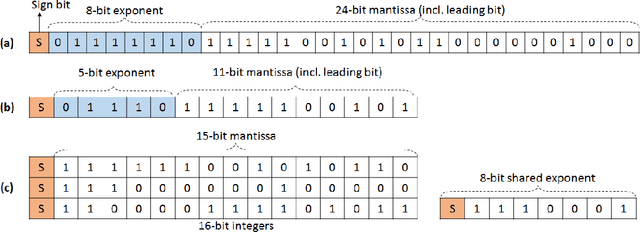
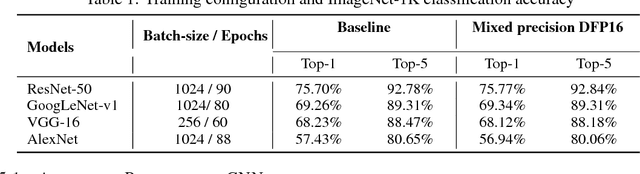
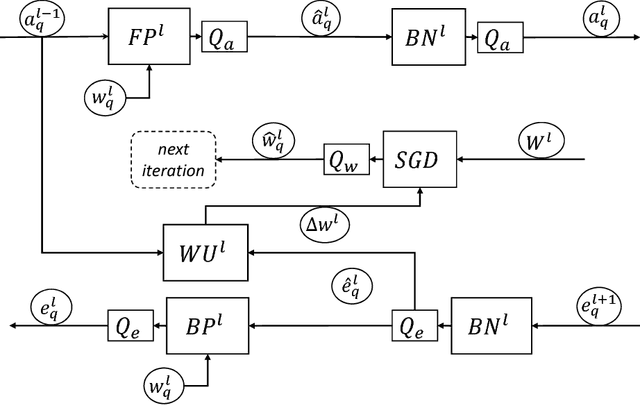
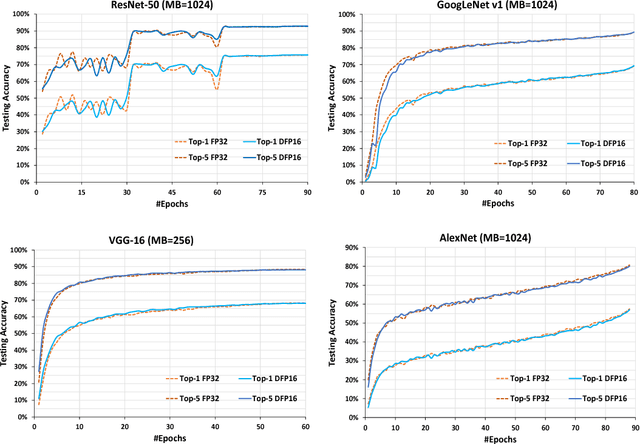
The state-of-the-art (SOTA) for mixed precision training is dominated by variants of low precision floating point operations, and in particular, FP16 accumulating into FP32 Micikevicius et al. (2017). On the other hand, while a lot of research has also happened in the domain of low and mixed-precision Integer training, these works either present results for non-SOTA networks (for instance only AlexNet for ImageNet-1K), or relatively small datasets (like CIFAR-10). In this work, we train state-of-the-art visual understanding neural networks on the ImageNet-1K dataset, with Integer operations on General Purpose (GP) hardware. In particular, we focus on Integer Fused-Multiply-and-Accumulate (FMA) operations which take two pairs of INT16 operands and accumulate results into an INT32 output.We propose a shared exponent representation of tensors and develop a Dynamic Fixed Point (DFP) scheme suitable for common neural network operations. The nuances of developing an efficient integer convolution kernel is examined, including methods to handle overflow of the INT32 accumulator. We implement CNN training for ResNet-50, GoogLeNet-v1, VGG-16 and AlexNet; and these networks achieve or exceed SOTA accuracy within the same number of iterations as their FP32 counterparts without any change in hyper-parameters and with a 1.8X improvement in end-to-end training throughput. To the best of our knowledge these results represent the first INT16 training results on GP hardware for ImageNet-1K dataset using SOTA CNNs and achieve highest reported accuracy using half-precision