Jennifer Gillenwater
Better Private Linear Regression Through Better Private Feature Selection
Jun 01, 2023



Abstract:Existing work on differentially private linear regression typically assumes that end users can precisely set data bounds or algorithmic hyperparameters. End users often struggle to meet these requirements without directly examining the data (and violating privacy). Recent work has attempted to develop solutions that shift these burdens from users to algorithms, but they struggle to provide utility as the feature dimension grows. This work extends these algorithms to higher-dimensional problems by introducing a differentially private feature selection method based on Kendall rank correlation. We prove a utility guarantee for the setting where features are normally distributed and conduct experiments across 25 datasets. We find that adding this private feature selection step before regression significantly broadens the applicability of ``plug-and-play'' private linear regression algorithms at little additional cost to privacy, computation, or decision-making by the end user.
Scalable Sampling for Nonsymmetric Determinantal Point Processes
Jan 20, 2022
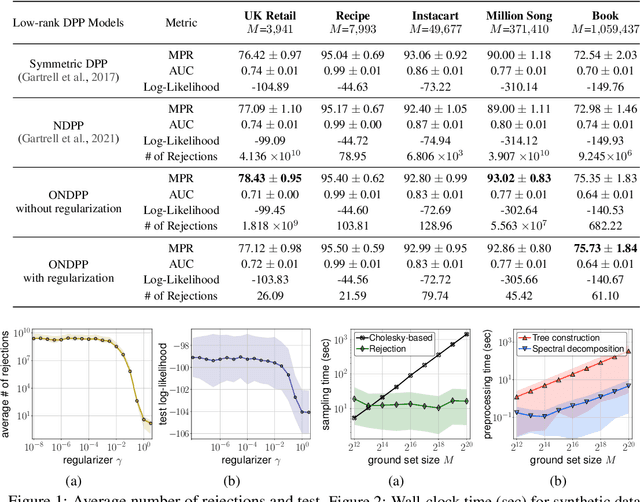
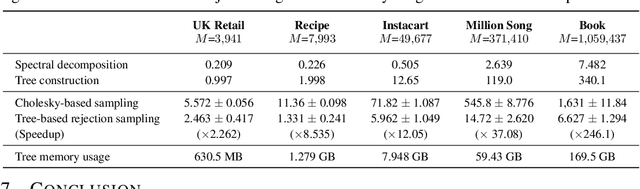
Abstract:A determinantal point process (DPP) on a collection of $M$ items is a model, parameterized by a symmetric kernel matrix, that assigns a probability to every subset of those items. Recent work shows that removing the kernel symmetry constraint, yielding nonsymmetric DPPs (NDPPs), can lead to significant predictive performance gains for machine learning applications. However, existing work leaves open the question of scalable NDPP sampling. There is only one known DPP sampling algorithm, based on Cholesky decomposition, that can directly apply to NDPPs as well. Unfortunately, its runtime is cubic in $M$, and thus does not scale to large item collections. In this work, we first note that this algorithm can be transformed into a linear-time one for kernels with low-rank structure. Furthermore, we develop a scalable sublinear-time rejection sampling algorithm by constructing a novel proposal distribution. Additionally, we show that imposing certain structural constraints on the NDPP kernel enables us to bound the rejection rate in a way that depends only on the kernel rank. In our experiments we compare the speed of all of these samplers for a variety of real-world tasks.
Combining Public and Private Data
Oct 29, 2021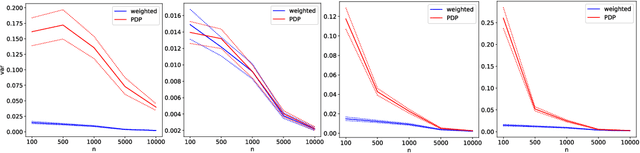
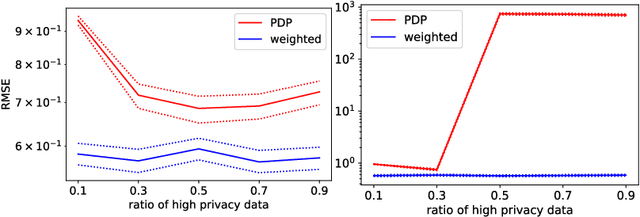
Abstract:Differential privacy is widely adopted to provide provable privacy guarantees in data analysis. We consider the problem of combining public and private data (and, more generally, data with heterogeneous privacy needs) for estimating aggregate statistics. We introduce a mixed estimator of the mean optimized to minimize the variance. We argue that our mechanism is preferable to techniques that preserve the privacy of individuals by subsampling data proportionally to the privacy needs of users. Similarly, we present a mixed median estimator based on the exponential mechanism. We compare our mechanisms to the methods proposed in Jorgensen et al. [2015]. Our experiments provide empirical evidence that our mechanisms often outperform the baseline methods.
Differentially Private Quantiles
Feb 16, 2021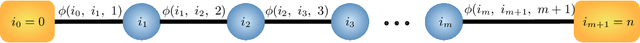

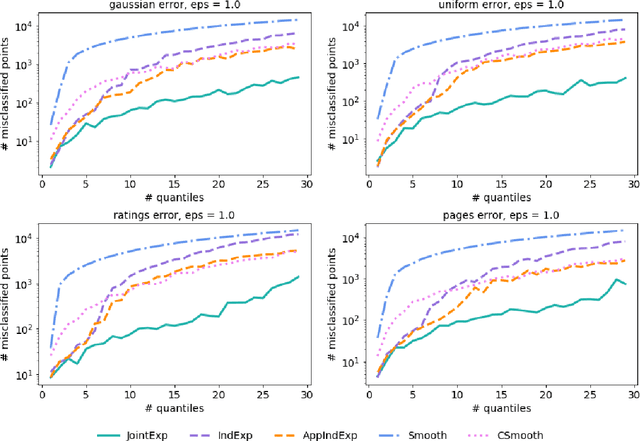
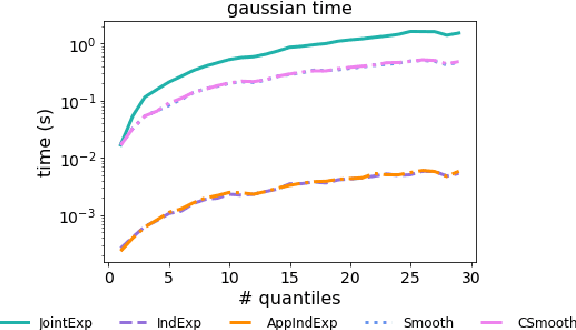
Abstract:Quantiles are often used for summarizing and understanding data. If that data is sensitive, it may be necessary to compute quantiles in a way that is differentially private, providing theoretical guarantees that the result does not reveal private information. However, in the common case where multiple quantiles are needed, existing differentially private algorithms scale poorly: they compute each quantile individually, splitting their privacy budget and thus decreasing accuracy. In this work we propose an instance of the exponential mechanism that simultaneously estimates $m$ quantiles from $n$ data points while guaranteeing differential privacy. The utility function is carefully structured to allow for an efficient implementation that avoids exponential dependence on $m$ and returns estimates of all $m$ quantiles in time $O(mn^2 + m^2n)$. Experiments show that our method significantly outperforms the current state of the art on both real and synthetic data while remaining efficient enough to be practical.
Federated Learning via Posterior Averaging: A New Perspective and Practical Algorithms
Oct 11, 2020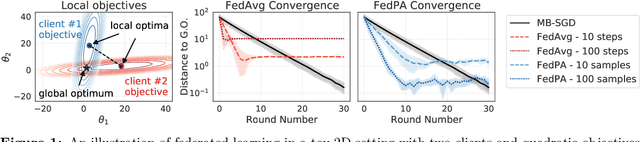

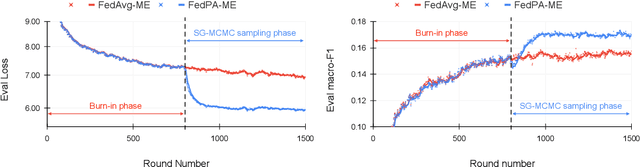
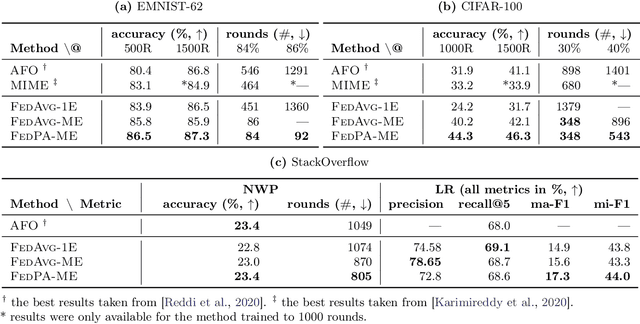
Abstract:Federated learning is typically approached as an optimization problem, where the goal is to minimize a global loss function by distributing computation across client devices that possess local data and specify different parts of the global objective. We present an alternative perspective and formulate federated learning as a posterior inference problem, where the goal is to infer a global posterior distribution by having client devices each infer the posterior of their local data. While exact inference is often intractable, this perspective provides a principled way to search for global optima in federated settings. Further, starting with the analysis of federated quadratic objectives, we develop a computation- and communication-efficient approximate posterior inference algorithm -- federated posterior averaging (FedPA). Our algorithm uses MCMC for approximate inference of local posteriors on the clients and efficiently communicates their statistics to the server, where the latter uses them to refine a global estimate of the posterior mode. Finally, we show that FedPA generalizes federated averaging (FedAvg), can similarly benefit from adaptive optimizers, and yields state-of-the-art results on four realistic and challenging benchmarks, converging faster, to better optima.
Scalable Learning and MAP Inference for Nonsymmetric Determinantal Point Processes
Jun 17, 2020
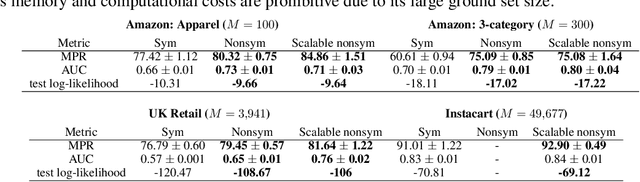
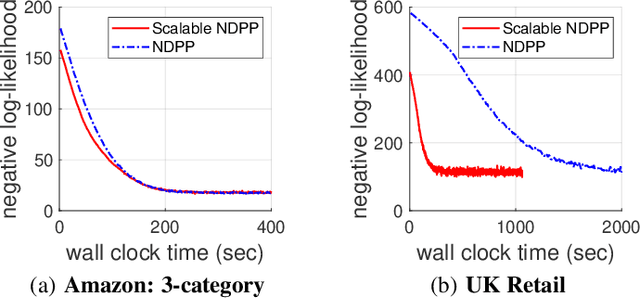
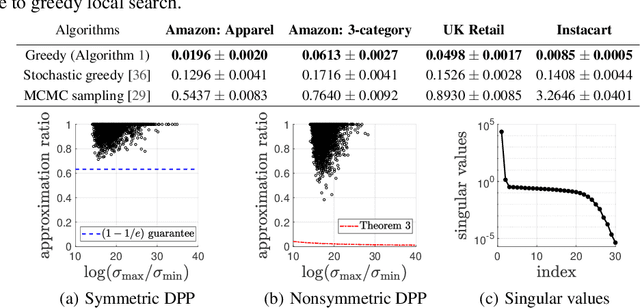
Abstract:Determinantal point processes (DPPs) have attracted significant attention from the machine learning community for their ability to model subsets drawn from a large collection of items. Recent work shows that nonsymmetric DPP kernels have significant advantages over symmetric kernels in terms of modeling power and predictive performance. However, the nonsymmetric kernel learning algorithm from prior work has computational complexity that is cubic in the size of the DPP ground set, from which subsets are drawn, making it impractical to use at large scales. In this work, we propose a new decomposition for nonsymmetric DPP kernels that induces linear-time complexity for learning and approximate maximum a posteriori (MAP) inference. We also prove a lower bound on the quality of this MAP approximation. Through evaluation on real-world datasets, we show that our new decomposition not only scales better, but also matches or exceeds the predictive performance of prior work.
Submodular Hamming Metrics
Nov 06, 2015


Abstract:We show that there is a largely unexplored class of functions (positive polymatroids) that can define proper discrete metrics over pairs of binary vectors and that are fairly tractable to optimize over. By exploiting submodularity, we are able to give hardness results and approximation algorithms for optimizing over such metrics. Additionally, we demonstrate empirically the effectiveness of these metrics and associated algorithms on both a metric minimization task (a form of clustering) and also a metric maximization task (generating diverse k-best lists).
Expectation-Maximization for Learning Determinantal Point Processes
Nov 04, 2014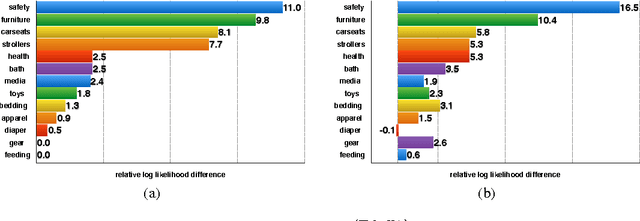

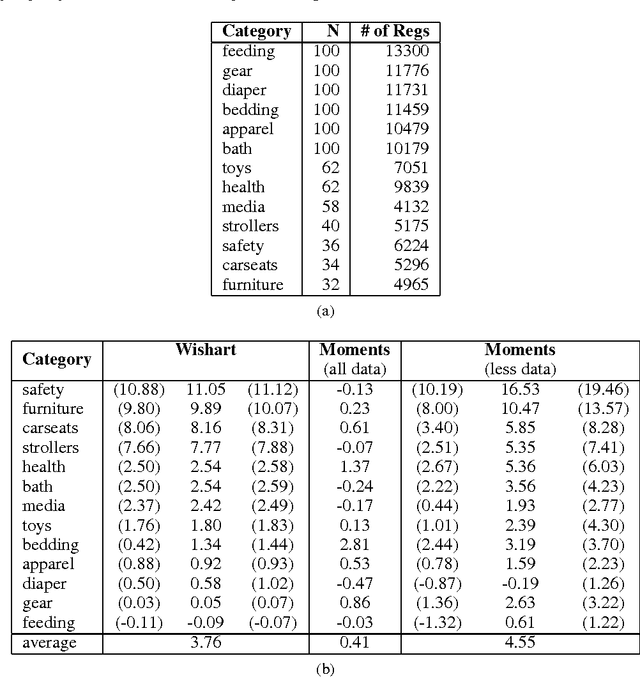
Abstract:A determinantal point process (DPP) is a probabilistic model of set diversity compactly parameterized by a positive semi-definite kernel matrix. To fit a DPP to a given task, we would like to learn the entries of its kernel matrix by maximizing the log-likelihood of the available data. However, log-likelihood is non-convex in the entries of the kernel matrix, and this learning problem is conjectured to be NP-hard. Thus, previous work has instead focused on more restricted convex learning settings: learning only a single weight for each row of the kernel matrix, or learning weights for a linear combination of DPPs with fixed kernel matrices. In this work we propose a novel algorithm for learning the full kernel matrix. By changing the kernel parameterization from matrix entries to eigenvalues and eigenvectors, and then lower-bounding the likelihood in the manner of expectation-maximization algorithms, we obtain an effective optimization procedure. We test our method on a real-world product recommendation task, and achieve relative gains of up to 16.5% in test log-likelihood compared to the naive approach of maximizing likelihood by projected gradient ascent on the entries of the kernel matrix.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge