Boosting CNN-based Handwriting Recognition Systems with Learnable Relaxation Labeling

The primary challenge for handwriting recognition systems lies in managing long-range contextual dependencies, an issue that traditional models often struggle with. To mitigate it, attention mechanisms have recently been employed to enhance context-aware labelling, thereby achieving state-of-the-art performance. In the field of pattern recognition and image analysis, however, the use of contextual information in labelling problems has a long history and goes back at least to the early 1970's. Among the various approaches developed in those years, Relaxation Labelling (RL) processes have played a prominent role and have been the method of choice in the field for more than a decade. Contrary to recent transformer-based architectures, RL processes offer a principled approach to the use of contextual constraints, having a solid theoretic foundation grounded on variational inequality and game theory, as well as effective algorithms with convergence guarantees. In this paper, we propose a novel approach to handwriting recognition that integrates the strengths of two distinct methodologies. In particular, we propose integrating (trainable) RL processes with various well-established neural architectures and we introduce a sparsification technique that accelerates the convergence of the algorithm and enhances the overall system's performance. Experiments over several benchmark datasets show that RL processes can improve the generalisation ability, even surpassing in some cases transformer-based architectures.

Measuring Orthogonality in Representations of Generative Models

In unsupervised representation learning, models aim to distill essential features from high-dimensional data into lower-dimensional learned representations, guided by inductive biases. Understanding the characteristics that make a good representation remains a topic of ongoing research. Disentanglement of independent generative processes has long been credited with producing high-quality representations. However, focusing solely on representations that adhere to the stringent requirements of most disentanglement metrics, may result in overlooking many high-quality representations, well suited for various downstream tasks. These metrics often demand that generative factors be encoded in distinct, single dimensions aligned with the canonical basis of the representation space. Motivated by these observations, we propose two novel metrics: Importance-Weighted Orthogonality (IWO) and Importance-Weighted Rank (IWR). These metrics evaluate the mutual orthogonality and rank of generative factor subspaces. Throughout extensive experiments on common downstream tasks, over several benchmark datasets and models, IWO and IWR consistently show stronger correlations with downstream task performance than traditional disentanglement metrics. Our findings suggest that representation quality is closer related to the orthogonality of independent generative processes rather than their disentanglement, offering a new direction for evaluating and improving unsupervised learning models.

Multi-Phase Relaxation Labeling for Square Jigsaw Puzzle Solving

We present a novel method for solving square jigsaw puzzles based on global optimization. The method is fully automatic, assumes no prior information, and can handle puzzles with known or unknown piece orientation. At the core of the optimization process is nonlinear relaxation labeling, a well-founded approach for deducing global solutions from local constraints, but unlike the classical scheme here we propose a multi-phase approach that guarantees convergence to feasible puzzle solutions. Next to the algorithmic novelty, we also present a new compatibility function for the quantification of the affinity between adjacent puzzle pieces. Competitive results and the advantage of the multi-phase approach are demonstrated on standard datasets.

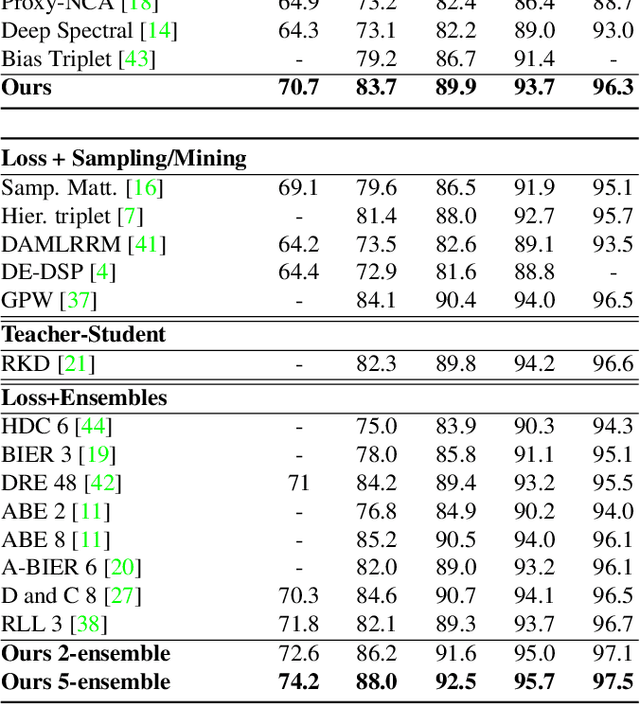
The Group Loss++: A deeper look into group loss for deep metric learning

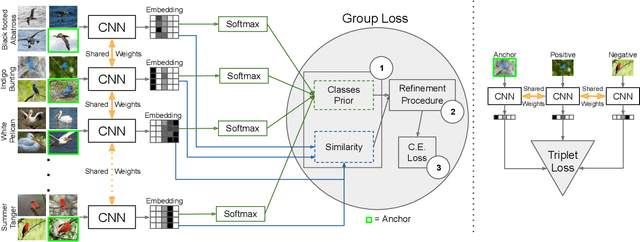
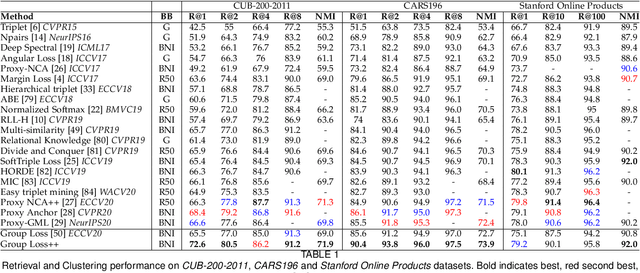
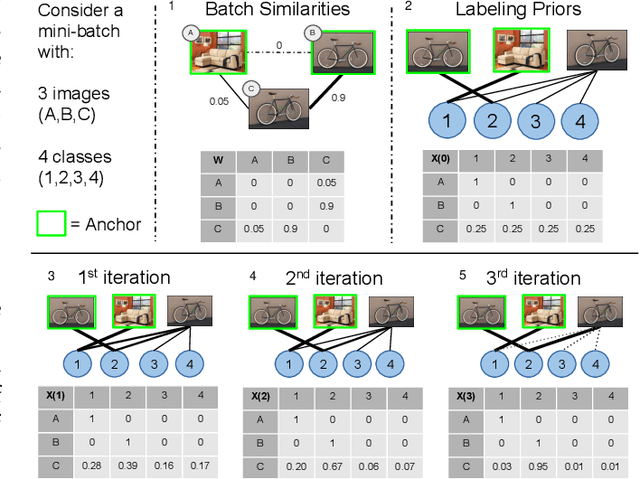
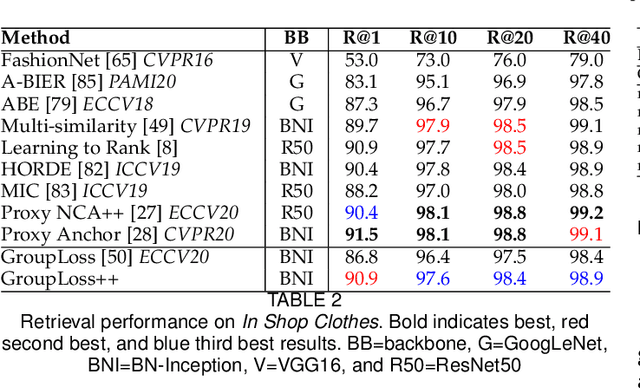
Deep metric learning has yielded impressive results in tasks such as clustering and image retrieval by leveraging neural networks to obtain highly discriminative feature embeddings, which can be used to group samples into different classes. Much research has been devoted to the design of smart loss functions or data mining strategies for training such networks. Most methods consider only pairs or triplets of samples within a mini-batch to compute the loss function, which is commonly based on the distance between embeddings. We propose Group Loss, a loss function based on a differentiable label-propagation method that enforces embedding similarity across all samples of a group while promoting, at the same time, low-density regions amongst data points belonging to different groups. Guided by the smoothness assumption that "similar objects should belong to the same group", the proposed loss trains the neural network for a classification task, enforcing a consistent labelling amongst samples within a class. We design a set of inference strategies tailored towards our algorithm, named Group Loss++ that further improve the results of our model. We show state-of-the-art results on clustering and image retrieval on four retrieval datasets, and present competitive results on two person re-identification datasets, providing a unified framework for retrieval and re-identification.

A Black-box Adversarial Attack for Poisoning Clustering

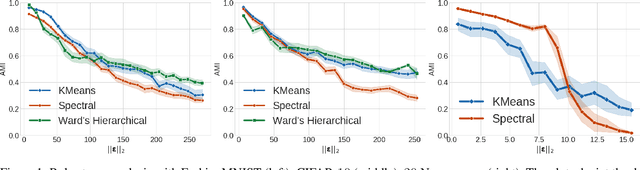
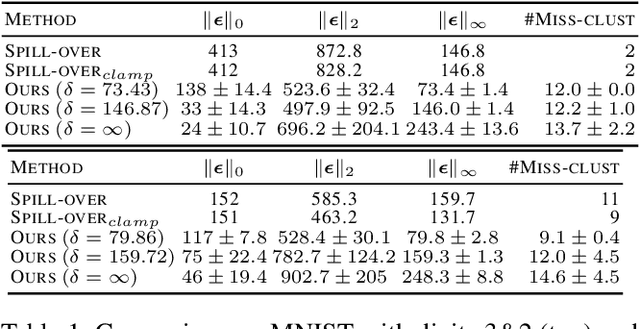
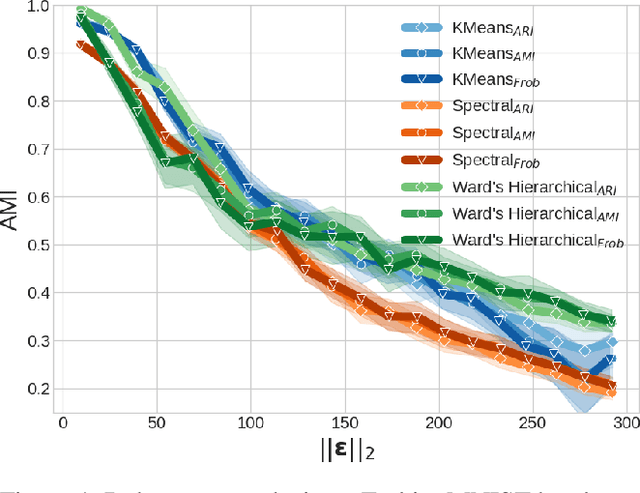
Clustering algorithms play a fundamental role as tools in decision-making and sensible automation processes. Due to the widespread use of these applications, a robustness analysis of this family of algorithms against adversarial noise has become imperative. To the best of our knowledge, however, only a few works have currently addressed this problem. In an attempt to fill this gap, in this work, we propose a black-box adversarial attack for crafting adversarial samples to test the robustness of clustering algorithms. We formulate the problem as a constrained minimization program, general in its structure and customizable by the attacker according to her capability constraints. We do not assume any information about the internal structure of the victim clustering algorithm, and we allow the attacker to query it as a service only. In the absence of any derivative information, we perform the optimization with a custom approach inspired by the Abstract Genetic Algorithm (AGA). In the experimental part, we demonstrate the sensibility of different single and ensemble clustering algorithms against our crafted adversarial samples on different scenarios. Furthermore, we perform a comparison of our algorithm with a state-of-the-art approach showing that we are able to reach or even outperform its performance. Finally, to highlight the general nature of the generated noise, we show that our attacks are transferable even against supervised algorithms such as SVMs, random forests and neural networks.

The Group Loss for Deep Metric Learning

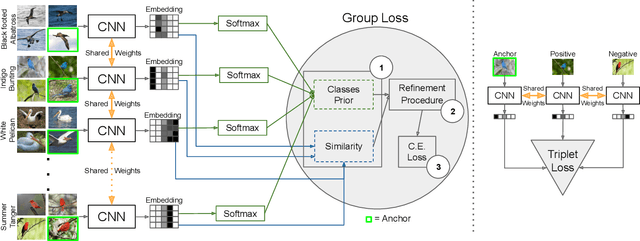
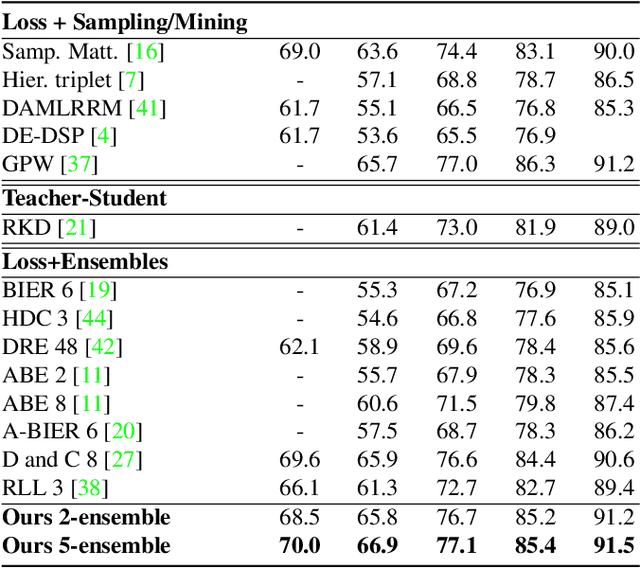
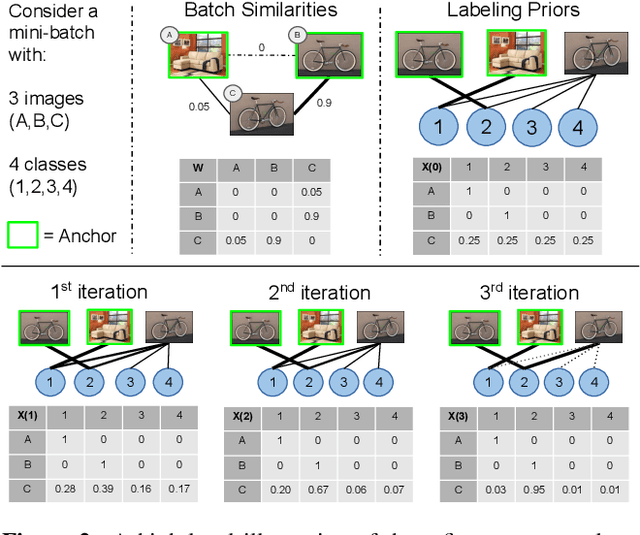
Deep metric learning has yielded impressive results in tasks such as clustering and image retrieval by leveraging neural networks to obtain highly discriminative feature embeddings, which can be used to group samples into different classes. Much research has been devoted to the design of smart loss functions or data mining strategies for training such networks. Most methods consider only pairs or triplets of samples within a mini-batch to compute the loss function, which is commonly based on the distance between embeddings. We propose Group Loss, a loss function based on a differentiable label-propagation method that enforces embedding similarity across all samples of a group while promoting, at the same time, low-density regions amongst data points belonging to different groups. Guided by the smoothness assumption that "similar objects should belong to the same group", the proposed loss trains the neural network for a classification task, enforcing a consistent labelling amongst samples within a class. We show state-of-the-art results on clustering and image retrieval on several datasets, and show the potential of our method when combined with other techniques such as ensembles

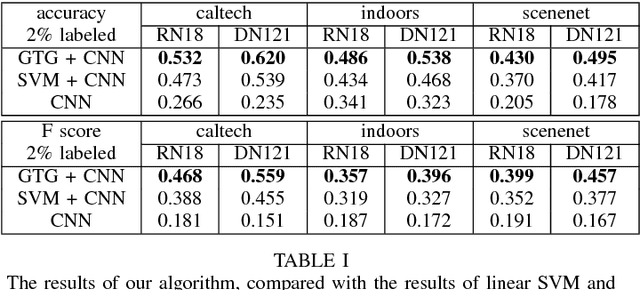
Unsupervised Domain Adaptation using Graph Transduction Games

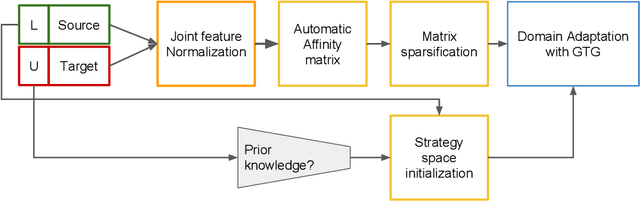
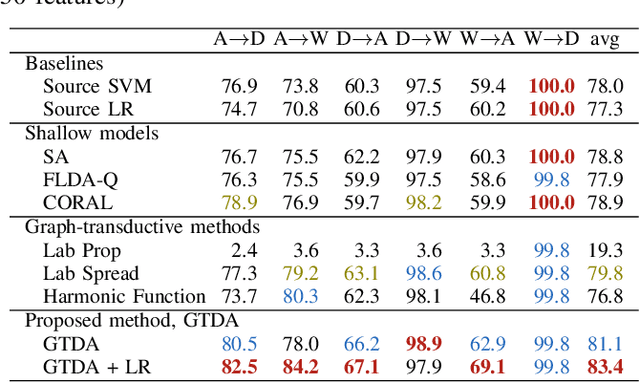
Unsupervised domain adaptation (UDA) amounts to assigning class labels to the unlabeled instances of a dataset from a target domain, using labeled instances of a dataset from a related source domain. In this paper, we propose to cast this problem in a game-theoretic setting as a non-cooperative game and introduce a fully automatized iterative algorithm for UDA based on graph transduction games (GTG). The main advantages of this approach are its principled foundation, guaranteed termination of the iterative algorithms to a Nash equilibrium (which corresponds to a consistent labeling condition) and soft labels quantifying the uncertainty of the label assignment process. We also investigate the beneficial effect of using pseudo-labels from linear classifiers to initialize the iterative process. The performance of the resulting methods is assessed on publicly available object recognition benchmark datasets involving both shallow and deep features. Results of experiments demonstrate the suitability of the proposed game-theoretic approach for solving UDA tasks.

Transductive Label Augmentation for Improved Deep Network Learning

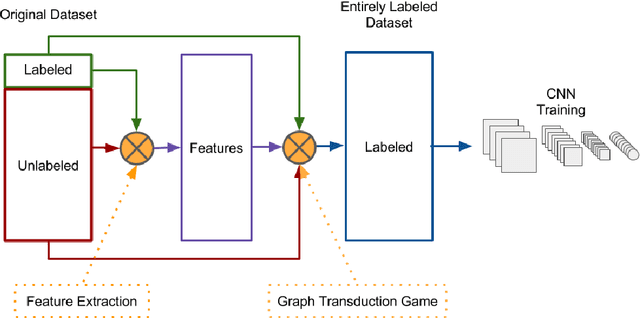
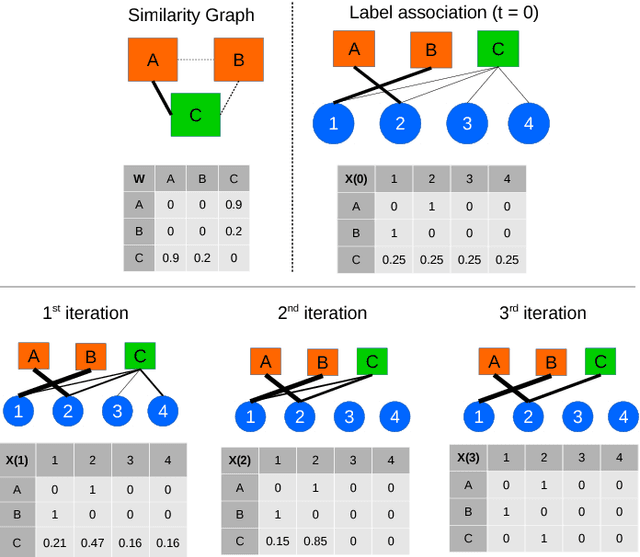
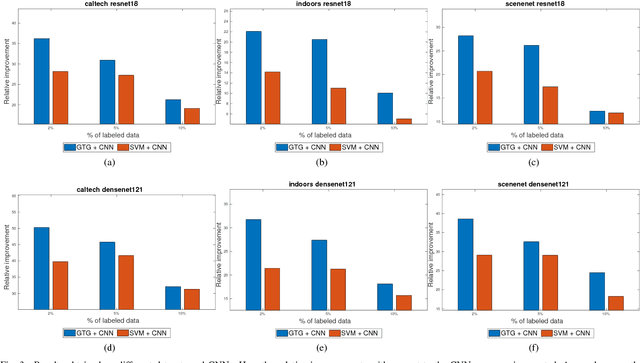
A major impediment to the application of deep learning to real-world problems is the scarcity of labeled data. Small training sets are in fact of no use to deep networks as, due to the large number of trainable parameters, they will very likely be subject to overfitting phenomena. On the other hand, the increment of the training set size through further manual or semi-automatic labellings can be costly, if not possible at times. Thus, the standard techniques to address this issue are transfer learning and data augmentation, which consists of applying some sort of "transformation" to existing labeled instances to let the training set grow in size. Although this approach works well in applications such as image classification, where it is relatively simple to design suitable transformation operators, it is not obvious how to apply it in more structured scenarios. Motivated by the observation that in virtually all application domains it is easy to obtain unlabeled data, in this paper we take a different perspective and propose a \emph{label augmentation} approach. We start from a small, curated labeled dataset and let the labels propagate through a larger set of unlabeled data using graph transduction techniques. This allows us to naturally use (second-order) similarity information which resides in the data, a source of information which is typically neglected by standard augmentation techniques. In particular, we show that by using known game theoretic transductive processes we can create larger and accurate enough labeled datasets which use results in better trained neural networks. Preliminary experiments are reported which demonstrate a consistent improvement over standard image classification datasets.

On the Interplay between Strong Regularity and Graph Densification

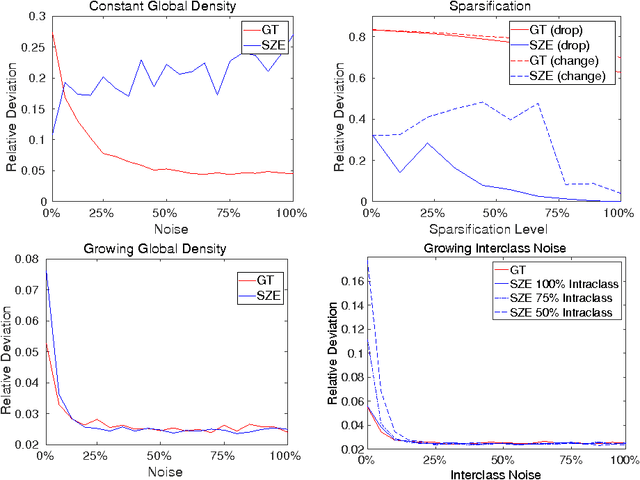
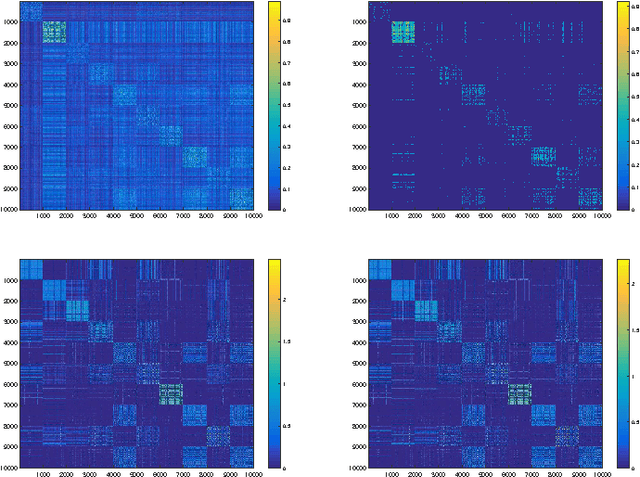
In this paper we analyze the practical implications of Szemer\'edi's regularity lemma in the preservation of metric information contained in large graphs. To this end, we present a heuristic algorithm to find regular partitions. Our experiments show that this method is quite robust to the natural sparsification of proximity graphs. In addition, this robustness can be enforced by graph densification.