Exploration--Exploitation in MDPs with Options

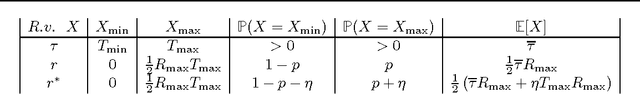
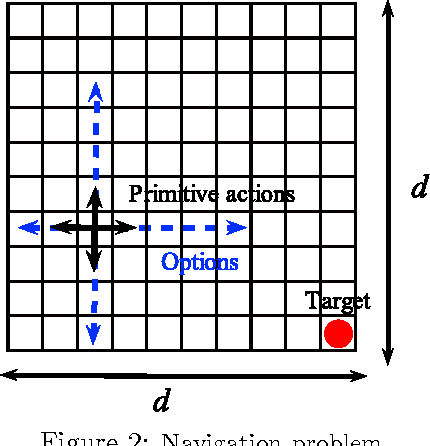
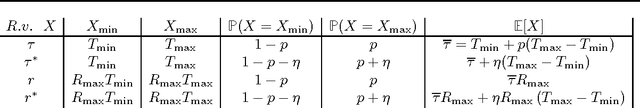
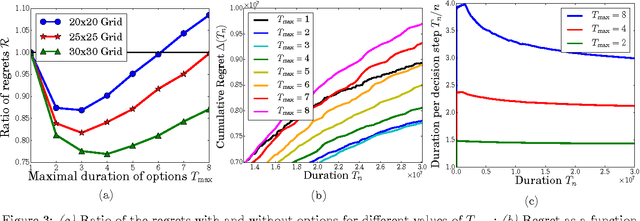
While a large body of empirical results show that temporally-extended actions and options may significantly affect the learning performance of an agent, the theoretical understanding of how and when options can be beneficial in online reinforcement learning is relatively limited. In this paper, we derive an upper and lower bound on the regret of a variant of UCRL using options. While we first analyze the algorithm in the general case of semi-Markov decision processes (SMDPs), we show how these results can be translated to the specific case of MDPs with options and we illustrate simple scenarios in which the regret of learning with options can be \textit{provably} much smaller than the regret suffered when learning with primitive actions.

Linear Thompson Sampling Revisited

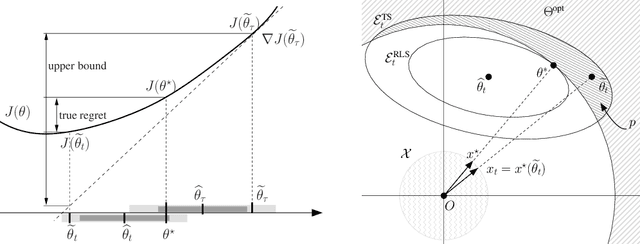
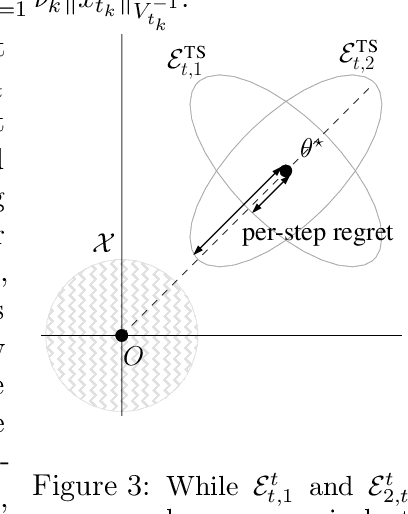
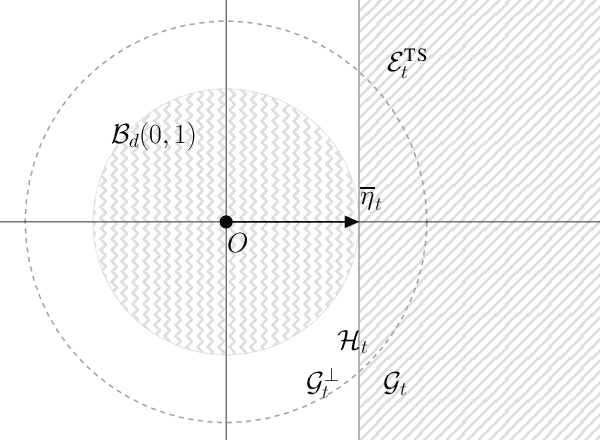
We derive an alternative proof for the regret of Thompson sampling (\ts) in the stochastic linear bandit setting. While we obtain a regret bound of order $\widetilde{O}(d^{3/2}\sqrt{T})$ as in previous results, the proof sheds new light on the functioning of the \ts. We leverage on the structure of the problem to show how the regret is related to the sensitivity (i.e., the gradient) of the objective function and how selecting optimal arms associated to \textit{optimistic} parameters does control it. Thus we show that \ts can be seen as a generic randomized algorithm where the sampling distribution is designed to have a fixed probability of being optimistic, at the cost of an additional $\sqrt{d}$ regret factor compared to a UCB-like approach. Furthermore, we show that our proof can be readily applied to regularized linear optimization and generalized linear model problems.

Thompson Sampling for Linear-Quadratic Control Problems

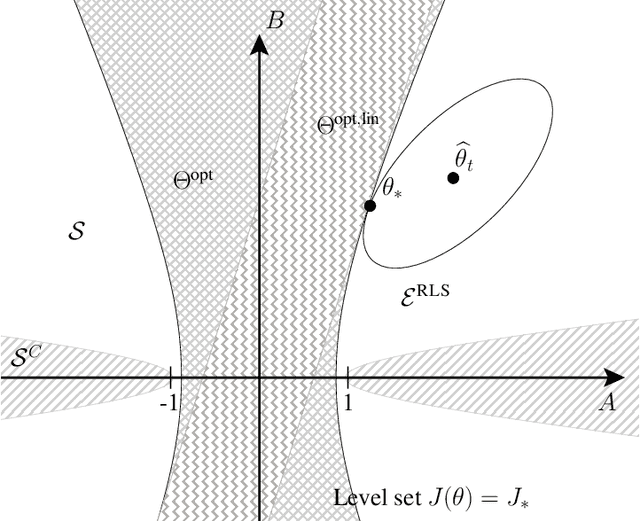
We consider the exploration-exploitation tradeoff in linear quadratic (LQ) control problems, where the state dynamics is linear and the cost function is quadratic in states and controls. We analyze the regret of Thompson sampling (TS) (a.k.a. posterior-sampling for reinforcement learning) in the frequentist setting, i.e., when the parameters characterizing the LQ dynamics are fixed. Despite the empirical and theoretical success in a wide range of problems from multi-armed bandit to linear bandit, we show that when studying the frequentist regret TS in control problems, we need to trade-off the frequency of sampling optimistic parameters and the frequency of switches in the control policy. This results in an overall regret of $O(T^{2/3})$, which is significantly worse than the regret $O(\sqrt{T})$ achieved by the optimism-in-face-of-uncertainty algorithm in LQ control problems.

Analysis of Kelner and Levin graph sparsification algorithm for a streaming setting

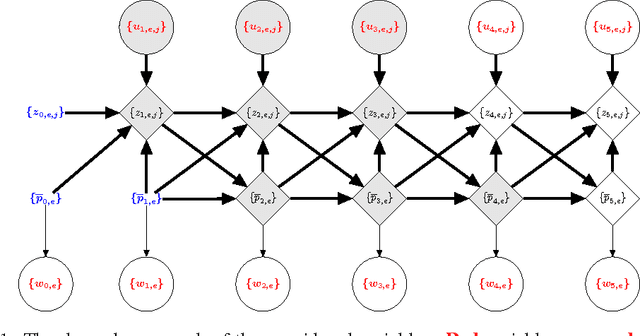
We derive a new proof to show that the incremental resparsification algorithm proposed by Kelner and Levin (2013) produces a spectral sparsifier in high probability. We rigorously take into account the dependencies across subsequent resparsifications using martingale inequalities, fixing a flaw in the original analysis.

Open Problem: Approximate Planning of POMDPs in the class of Memoryless Policies

Planning plays an important role in the broad class of decision theory. Planning has drawn much attention in recent work in the robotics and sequential decision making areas. Recently, Reinforcement Learning (RL), as an agent-environment interaction problem, has brought further attention to planning methods. Generally in RL, one can assume a generative model, e.g. graphical models, for the environment, and then the task for the RL agent is to learn the model parameters and find the optimal strategy based on these learnt parameters. Based on environment behavior, the agent can assume various types of generative models, e.g. Multi Armed Bandit for a static environment, or Markov Decision Process (MDP) for a dynamic environment. The advantage of these popular models is their simplicity, which results in tractable methods of learning the parameters and finding the optimal policy. The drawback of these models is again their simplicity: these models usually underfit and underestimate the actual environment behavior. For example, in robotics, the agent usually has noisy observations of the environment inner state and MDP is not a suitable model. More complex models like Partially Observable Markov Decision Process (POMDP) can compensate for this drawback. Fitting this model to the environment, where the partial observation is given to the agent, generally gives dramatic performance improvement, sometimes unbounded improvement, compared to MDP. In general, finding the optimal policy for the POMDP model is computationally intractable and fully non convex, even for the class of memoryless policies. The open problem is to come up with a method to find an exact or an approximate optimal stochastic memoryless policy for POMDP models.

Reinforcement Learning of POMDPs using Spectral Methods

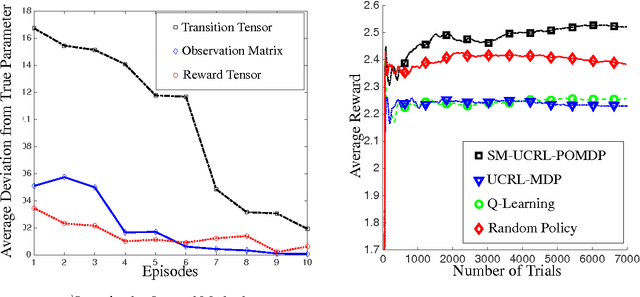
We propose a new reinforcement learning algorithm for partially observable Markov decision processes (POMDP) based on spectral decomposition methods. While spectral methods have been previously employed for consistent learning of (passive) latent variable models such as hidden Markov models, POMDPs are more challenging since the learner interacts with the environment and possibly changes the future observations in the process. We devise a learning algorithm running through episodes, in each episode we employ spectral techniques to learn the POMDP parameters from a trajectory generated by a fixed policy. At the end of the episode, an optimization oracle returns the optimal memoryless planning policy which maximizes the expected reward based on the estimated POMDP model. We prove an order-optimal regret bound with respect to the optimal memoryless policy and efficient scaling with respect to the dimensionality of observation and action spaces.

Incremental Spectral Sparsification for Large-Scale Graph-Based Semi-Supervised Learning

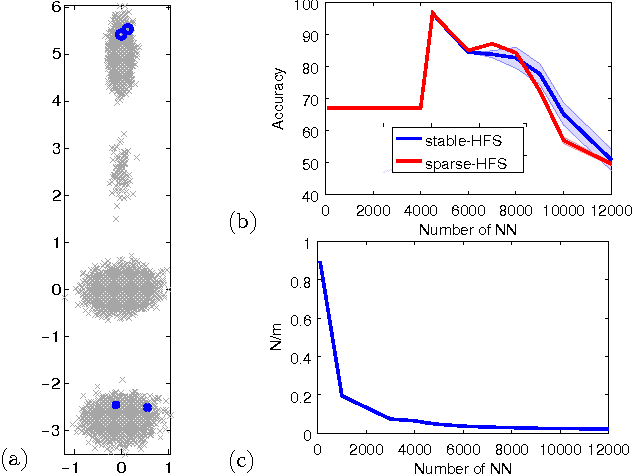
While the harmonic function solution performs well in many semi-supervised learning (SSL) tasks, it is known to scale poorly with the number of samples. Recent successful and scalable methods, such as the eigenfunction method focus on efficiently approximating the whole spectrum of the graph Laplacian constructed from the data. This is in contrast to various subsampling and quantization methods proposed in the past, which may fail in preserving the graph spectra. However, the impact of the approximation of the spectrum on the final generalization error is either unknown, or requires strong assumptions on the data. In this paper, we introduce Sparse-HFS, an efficient edge-sparsification algorithm for SSL. By constructing an edge-sparse and spectrally similar graph, we are able to leverage the approximation guarantees of spectral sparsification methods to bound the generalization error of Sparse-HFS. As a result, we obtain a theoretically-grounded approximation scheme for graph-based SSL that also empirically matches the performance of known large-scale methods.

Upper-Confidence-Bound Algorithms for Active Learning in Multi-Armed Bandits

In this paper, we study the problem of estimating uniformly well the mean values of several distributions given a finite budget of samples. If the variance of the distributions were known, one could design an optimal sampling strategy by collecting a number of independent samples per distribution that is proportional to their variance. However, in the more realistic case where the distributions are not known in advance, one needs to design adaptive sampling strategies in order to select which distribution to sample from according to the previously observed samples. We describe two strategies based on pulling the distributions a number of times that is proportional to a high-probability upper-confidence-bound on their variance (built from previous observed samples) and report a finite-sample performance analysis on the excess estimation error compared to the optimal allocation. We show that the performance of these allocation strategies depends not only on the variances but also on the full shape of the distributions.

Best-Arm Identification in Linear Bandits

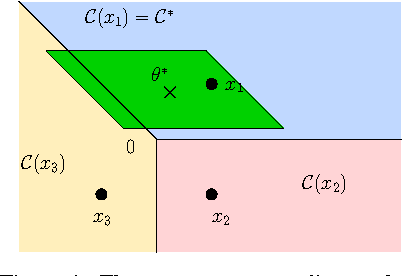
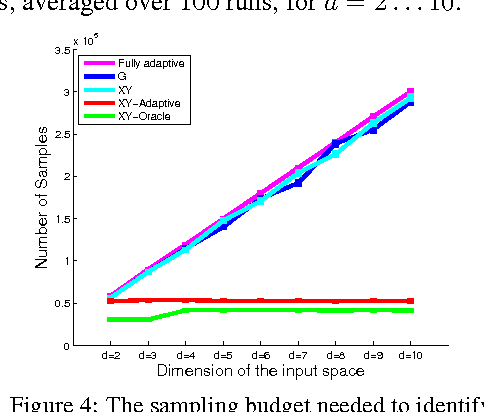
We study the best-arm identification problem in linear bandit, where the rewards of the arms depend linearly on an unknown parameter $\theta^*$ and the objective is to return the arm with the largest reward. We characterize the complexity of the problem and introduce sample allocation strategies that pull arms to identify the best arm with a fixed confidence, while minimizing the sample budget. In particular, we show the importance of exploiting the global linear structure to improve the estimate of the reward of near-optimal arms. We analyze the proposed strategies and compare their empirical performance. Finally, as a by-product of our analysis, we point out the connection to the $G$-optimality criterion used in optimal experimental design.

Online Stochastic Optimization under Correlated Bandit Feedback

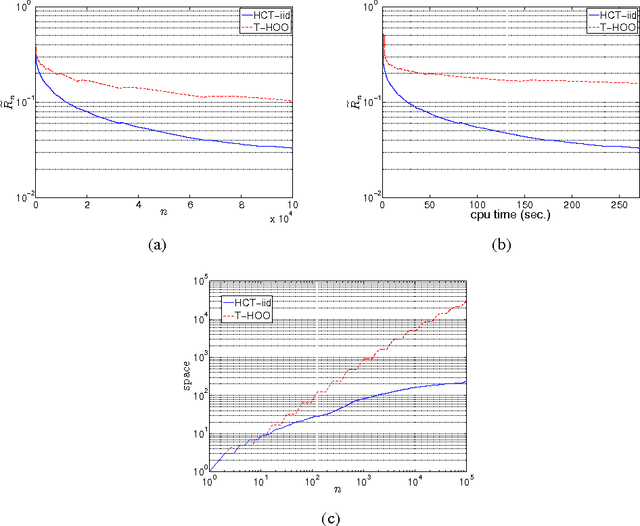
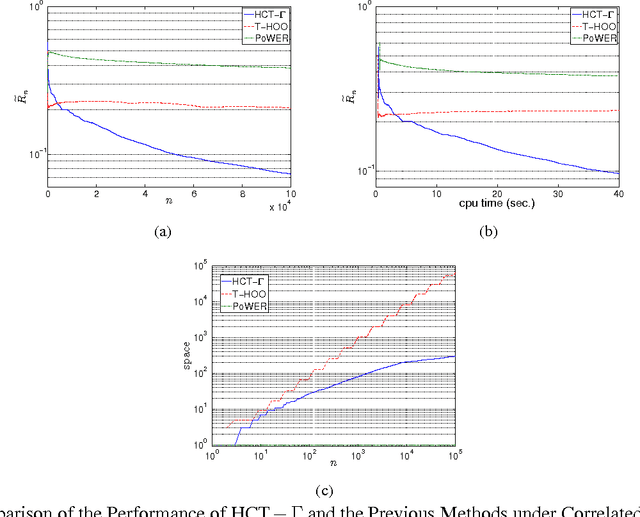
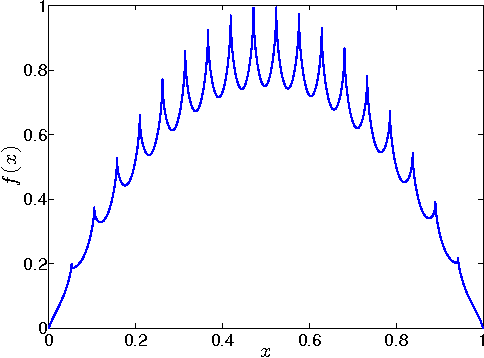
In this paper we consider the problem of online stochastic optimization of a locally smooth function under bandit feedback. We introduce the high-confidence tree (HCT) algorithm, a novel any-time $\mathcal{X}$-armed bandit algorithm, and derive regret bounds matching the performance of existing state-of-the-art in terms of dependency on number of steps and smoothness factor. The main advantage of HCT is that it handles the challenging case of correlated rewards, whereas existing methods require that the reward-generating process of each arm is an identically and independent distributed (iid) random process. HCT also improves on the state-of-the-art in terms of its memory requirement as well as requiring a weaker smoothness assumption on the mean-reward function in compare to the previous anytime algorithms. Finally, we discuss how HCT can be applied to the problem of policy search in reinforcement learning and we report preliminary empirical results.