ResearchRubrics: A Benchmark of Prompts and Rubrics For Evaluating Deep Research Agents

Deep Research (DR) is an emerging agent application that leverages large language models (LLMs) to address open-ended queries. It requires the integration of several capabilities, including multi-step reasoning, cross-document synthesis, and the generation of evidence-backed, long-form answers. Evaluating DR remains challenging because responses are lengthy and diverse, admit many valid solutions, and often depend on dynamic information sources. We introduce ResearchRubrics, a standardized benchmark for DR built with over 2,800+ hours of human labor that pairs realistic, domain-diverse prompts with 2,500+ expert-written, fine-grained rubrics to assess factual grounding, reasoning soundness, and clarity. We also propose a new complexity framework for categorizing DR tasks along three axes: conceptual breadth, logical nesting, and exploration. In addition, we develop human and model-based evaluation protocols that measure rubric adherence for DR agents. We evaluate several state-of-the-art DR systems and find that even leading agents like Gemini's DR and OpenAI's DR achieve under 68% average compliance with our rubrics, primarily due to missed implicit context and inadequate reasoning about retrieved information. Our results highlight the need for robust, scalable assessment of deep research capabilities, to which end we release ResearchRubrics(including all prompts, rubrics, and evaluation code) to facilitate progress toward well-justified research assistants.

Zeroth-Order Topological Insights into Iterative Magnitude Pruning

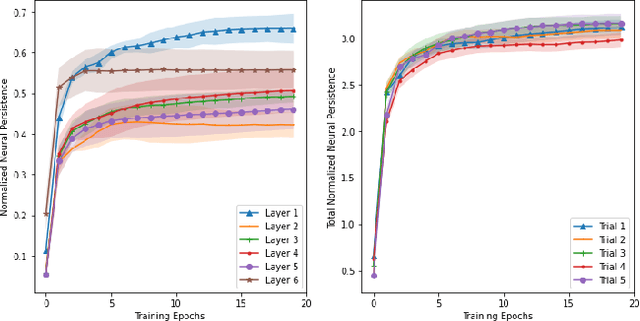
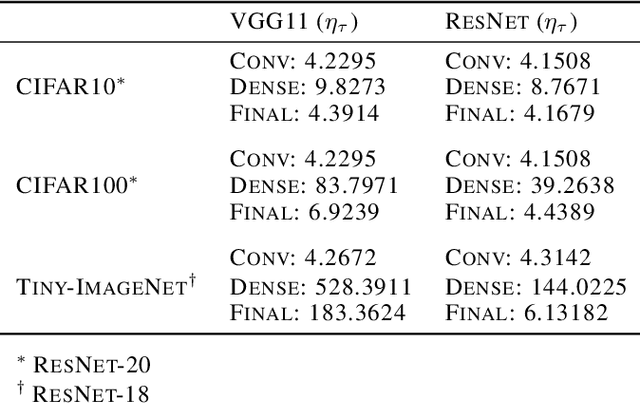
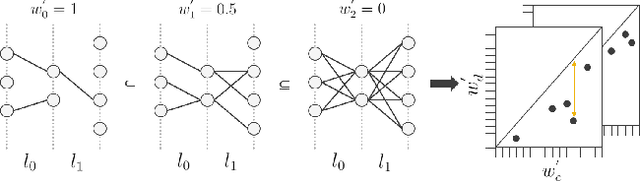
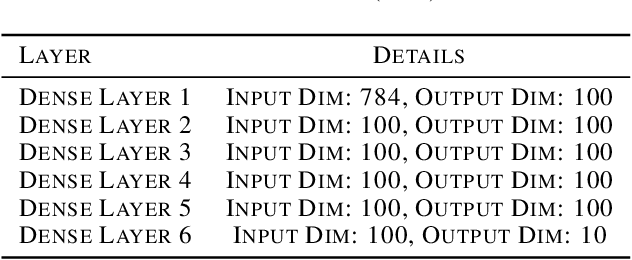
Modern-day neural networks are famously large, yet also highly redundant and compressible; there exist numerous pruning strategies in the deep learning literature that yield over 90% sparser sub-networks of fully-trained, dense architectures while still maintaining their original accuracies. Amongst these many methods though -- thanks to its conceptual simplicity, ease of implementation, and efficacy -- Iterative Magnitude Pruning (IMP) dominates in practice and is the de facto baseline to beat in the pruning community. However, theoretical explanations as to why a simplistic method such as IMP works at all are few and limited. In this work, we leverage the notion of persistent homology to gain insights into the workings of IMP and show that it inherently encourages retention of those weights which preserve topological information in a trained network. Subsequently, we also provide bounds on how much different networks can be pruned while perfectly preserving their zeroth order topological features, and present a modified version of IMP to do the same.