Ahmadreza Marandi
Efficient Sensitivity Analysis for Parametric Robust Markov Chains
May 01, 2023Abstract:We provide a novel method for sensitivity analysis of parametric robust Markov chains. These models incorporate parameters and sets of probability distributions to alleviate the often unrealistic assumption that precise probabilities are available. We measure sensitivity in terms of partial derivatives with respect to the uncertain transition probabilities regarding measures such as the expected reward. As our main contribution, we present an efficient method to compute these partial derivatives. To scale our approach to models with thousands of parameters, we present an extension of this method that selects the subset of $k$ parameters with the highest partial derivative. Our methods are based on linear programming and differentiating these programs around a given value for the parameters. The experiments show the applicability of our approach on models with over a million states and thousands of parameters. Moreover, we embed the results within an iterative learning scheme that profits from having access to a dedicated sensitivity analysis.
Robust Finite-State Controllers for Uncertain POMDPs
Sep 24, 2020
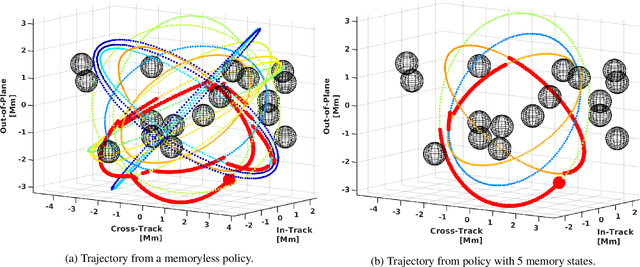
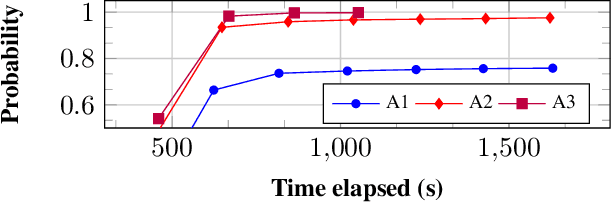
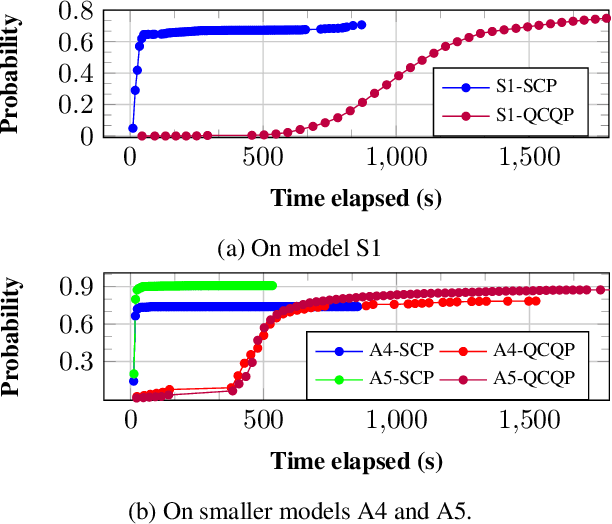
Abstract:Uncertain partially observable Markov decision processes (uPOMDPs) allow the probabilistic transition and observation functions of standard POMDPs to belong to a so-called uncertainty set. Such uncertainty sets capture uncountable sets of probability distributions. We develop an algorithm to compute finite-memory policies for uPOMDPs that robustly satisfy given specifications against any admissible distribution. In general, computing such policies is both theoretically and practically intractable. We provide an efficient solution to this problem in four steps. (1) We state the underlying problem as a nonconvex optimization problem with infinitely many constraints. (2) A dedicated dualization scheme yields a dual problem that is still nonconvex but has finitely many constraints. (3) We linearize this dual problem and (4) solve the resulting finite linear program to obtain locally optimal solutions to the original problem. The resulting problem formulation is exponentially smaller than those resulting from existing methods. We demonstrate the applicability of our algorithm using large instances of an aircraft collision-avoidance scenario and a novel spacecraft motion planning case study.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge