Robust Finite-State Controllers for Uncertain POMDPs
Paper and Code
Sep 24, 2020
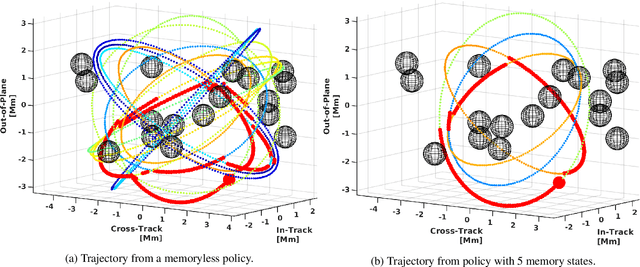
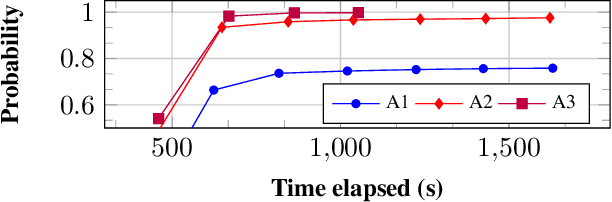
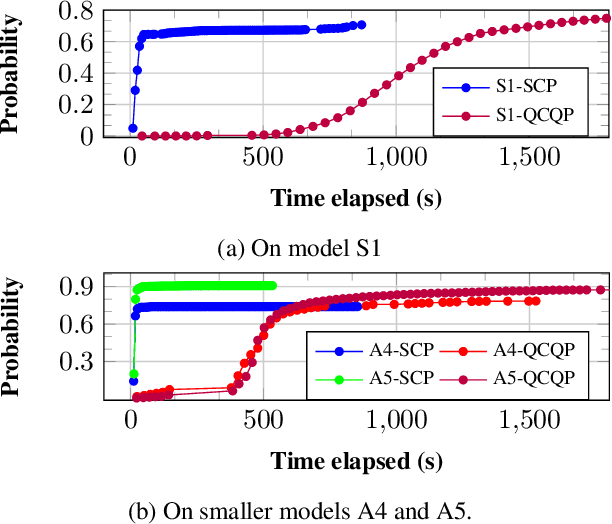
Uncertain partially observable Markov decision processes (uPOMDPs) allow the probabilistic transition and observation functions of standard POMDPs to belong to a so-called uncertainty set. Such uncertainty sets capture uncountable sets of probability distributions. We develop an algorithm to compute finite-memory policies for uPOMDPs that robustly satisfy given specifications against any admissible distribution. In general, computing such policies is both theoretically and practically intractable. We provide an efficient solution to this problem in four steps. (1) We state the underlying problem as a nonconvex optimization problem with infinitely many constraints. (2) A dedicated dualization scheme yields a dual problem that is still nonconvex but has finitely many constraints. (3) We linearize this dual problem and (4) solve the resulting finite linear program to obtain locally optimal solutions to the original problem. The resulting problem formulation is exponentially smaller than those resulting from existing methods. We demonstrate the applicability of our algorithm using large instances of an aircraft collision-avoidance scenario and a novel spacecraft motion planning case study.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge