AG-CVG: Coverage Planning with a Mobile Recharging UGV and an Energy-Constrained UAV

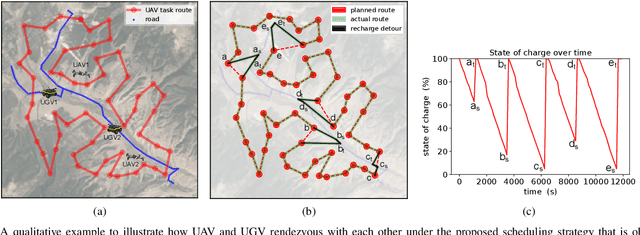
In this paper, we present an approach for coverage path planning for a team of an energy-constrained Unmanned Aerial Vehicle (UAV) and an Unmanned Ground Vehicle (UGV). Both the UAV and the UGV have predefined areas that they have to cover. The goal is to perform complete coverage by both robots while minimizing the coverage time. The UGV can also serve as a mobile recharging station. The UAV and UGV need to occasionally rendezvous for recharging. We propose a heuristic method to address this NP-Hard planning problem. Our approach involves initially determining coverage paths without factoring in energy constraints. Subsequently, we cluster segments of these paths and employ graph matching to assign UAV clusters to UGV clusters for efficient recharging management. We perform numerical analysis on real-world coverage applications and show that compared with a greedy approach our method reduces rendezvous overhead on average by 11.33\%. We demonstrate proof-of-concept with a team of a VOXL m500 drone and a Clearpath Jackal ground vehicle, providing a complete system from the offline algorithm to the field execution.

Energy-Aware Route Planning for a Battery-Constrained Robot with Multiple Charging Depots

This paper considers energy-aware route planning for a battery-constrained robot operating in environments with multiple recharging depots. The robot has a battery discharge time $D$, and it should visit the recharging depots at most every $D$ time units to not run out of charge. The objective is to minimize robot's travel time while ensuring it visits all task locations in the environment. We present a $O(\log D)$ approximation algorithm for this problem. We also present heuristic improvements to the approximation algorithm and assess its performance on instances from TSPLIB, comparing it to an optimal solution obtained through Integer Linear Programming (ILP). The simulation results demonstrate that, despite a more than $20$-fold reduction in runtime, the proposed algorithm provides solutions that are, on average, within $31\%$ of the ILP solution.

Where to Drop Sensors from Aerial Robots to Monitor a Surface-Level Phenomenon?

We consider the problem of routing a team of energy-constrained Unmanned Aerial Vehicles (UAVs) to drop unmovable sensors for monitoring a task area in the presence of stochastic wind disturbances. In prior work on mobile sensor routing problems, sensors and their carrier are one integrated platform, and sensors are assumed to be able to take measurements at exactly desired locations. By contrast, airdropping the sensors onto the ground can introduce stochasticity in the landing locations of the sensors. We focus on addressing this stochasticity in sensor locations from the path-planning perspective. Specifically, we formulate the problem (Multi-UAV Sensor Drop) as a variant of the Submodular Team Orienteering Problem with one additional constraint on the number of sensors on each UAV. The objective is to maximize the Mutual Information between the phenomenon at Points of Interest (PoIs) and the measurements that sensors will take at stochastic locations. We show that such an objective is computationally expensive to evaluate. To tackle this challenge, we propose a surrogate objective with a closed-form expression based on the expected mean and expected covariance of the Gaussian Process. We propose a heuristic algorithm to solve the optimization problem with the surrogate objective. The formulation and the algorithms are validated through extensive simulations.

Multi-Robot Persistent Monitoring: Minimizing Latency and Number of Robots with Recharging Constraints

In this paper we study multi-robot path planning for persistent monitoring tasks. We consider the case where robots have a limited battery capacity with a discharge time $D$. We represent the areas to be monitored as the vertices of a weighted graph. For each vertex, there is a constraint on the maximum allowable time between robot visits, called the latency. The objective is to find the minimum number of robots that can satisfy these latency constraints while also ensuring that the robots periodically charge at a recharging depot. The decision version of this problem is known to be PSPACE-complete. We present a $O(\frac{\log D}{\log \log D}\log \rho)$ approximation algorithm for the problem where $\rho$ is the ratio of the maximum and the minimum latency constraints. We also present an orienteering based heuristic to solve the problem and show empirically that it typically provides higher quality solutions than the approximation algorithm. We extend our results to provide an algorithm for the problem of minimizing the maximum weighted latency given a fixed number of robots. We evaluate our algorithms on large problem instances in a patrolling scenario and in a wildfire monitoring application. We also compare the algorithms with an existing solver on benchmark instances.

Risk-aware Resource Allocation for Multiple UAVs-UGVs Recharging Rendezvous

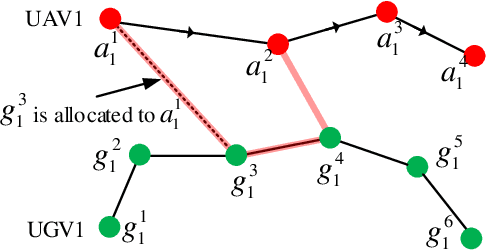
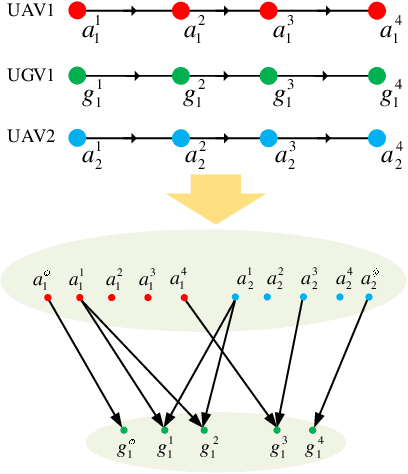
We study a resource allocation problem for the cooperative aerial-ground vehicle routing application, in which multiple Unmanned Aerial Vehicles (UAVs) with limited battery capacity and multiple Unmanned Ground Vehicles (UGVs) that can also act as a mobile recharging stations need to jointly accomplish a mission such as persistently monitoring a set of points. Due to the limited battery capacity of the UAVs, they sometimes have to deviate from their task to rendezvous with the UGVs and get recharged. Each UGV can serve a limited number of UAVs at a time. In contrast to prior work on deterministic multi-robot scheduling, we consider the challenge imposed by the stochasticity of the energy consumption of the UAV. We are interested in finding the optimal recharging schedule of the UAVs such that the travel cost is minimized and the probability that no UAV runs out of charge within the planning horizon is greater than a user-defined tolerance. We formulate this problem ({Risk-aware Recharging Rendezvous Problem (RRRP))} as an Integer Linear Program (ILP), in which the matching constraint captures the resource availability constraints and the knapsack constraint captures the success probability constraints. We propose a bicriteria approximation algorithm to solve RRRP. We demonstrate the effectiveness of our formulation and algorithm in the context of one persistent monitoring mission.

Risk-aware UAV-UGV Rendezvous with Chance-Constrained Markov Decision Process

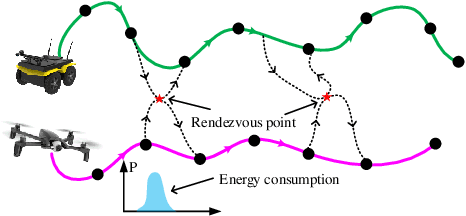
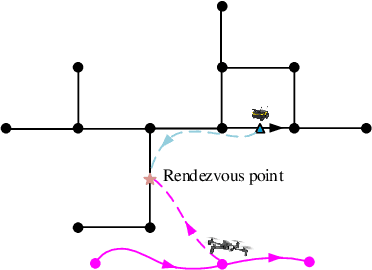
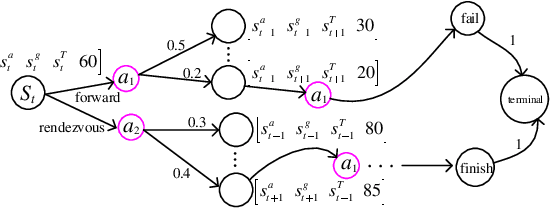
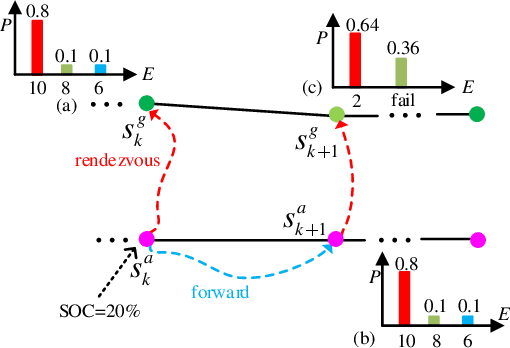
We study a chance-constrained variant of the cooperative aerial-ground vehicle routing problem, in which an Unmanned Aerial Vehicle (UAV) with limited battery capacity and an Unmanned Ground Vehicle (UGV) that can also act as a mobile recharging station need to jointly accomplish a mission such as monitoring a set of points. Due to the limited battery capacity of the UAV, two vehicles sometimes have to deviate from their task to rendezvous and recharge the UAV\@. Unlike prior work that has focused on the deterministic case, we address the challenge of stochastic energy consumption of the UAV\@. We are interested in finding the optimal policy that decides when and where to rendezvous such that the expected travel time of the UAV is minimized and the probability of running out of charge is less than a user-defined tolerance. We formulate this problem as a Chance Constrained Markov Decision Process (CCMDP). To the best knowledge of the authors, this is the first CMDP-based formulation for the UAV-UGV routing problems under power consumption uncertainty. We adopt a Linear Programming (LP) based approach to solve the problem optimally. We demonstrate the effectiveness of our formulation in the context of an Intelligence Surveillance and Reconnaissance (ISR) mission.

Multi-Robot Routing for Persistent Monitoring with Latency Constraints

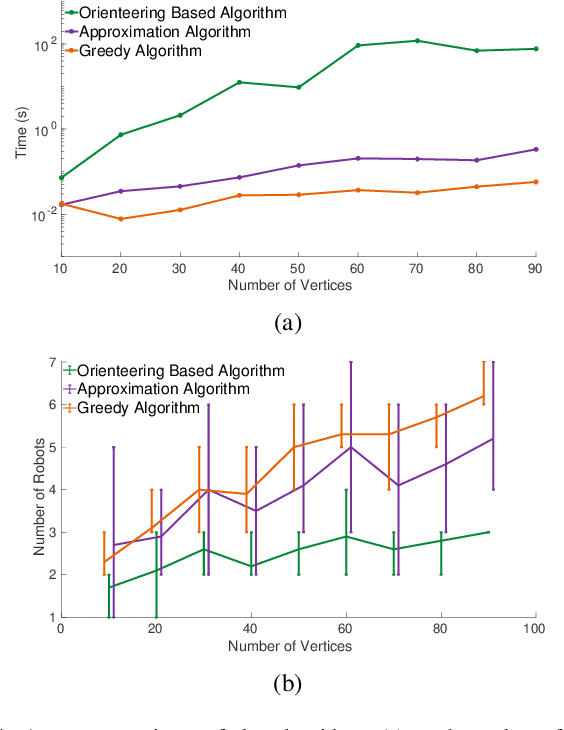
In this paper we study a multi-robot path planning problem for persistent monitoring of an environment. We represent the areas to be monitored as the vertices of a weighted graph. For each vertex, there is a constraint on the maximum time spent by the robots between visits to that vertex, called the latency, and the objective is to find the minimum number of robots that can satisfy these latency constraints. The decision version of this problem is known to be PSPACE-complete. We present a $O(\log \rho)$ approximation algorithm for the problem where $\rho$ is the ratio of the maximum and the minimum latency constraints. We also present an orienteering based heuristic to solve the problem and show through simulations that in most of the cases the heuristic algorithm gives better solutions than the approximation algorithm. We evaluate our algorithms on large problem instances in a patrolling scenario and in a persistent scene reconstruction application. We also compare the algorithms with an existing solver on benchmark instances.

Robot Monitoring for the Detection and Confirmation of Stochastic Events

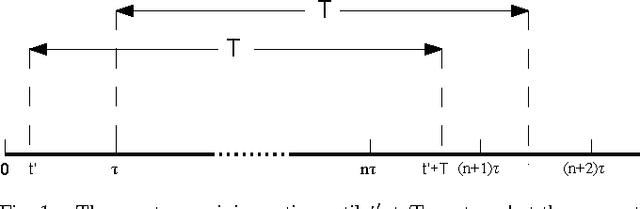
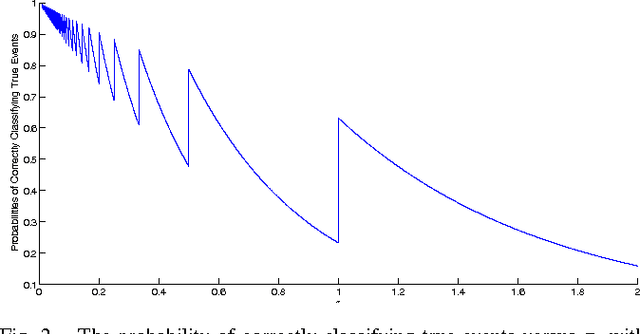
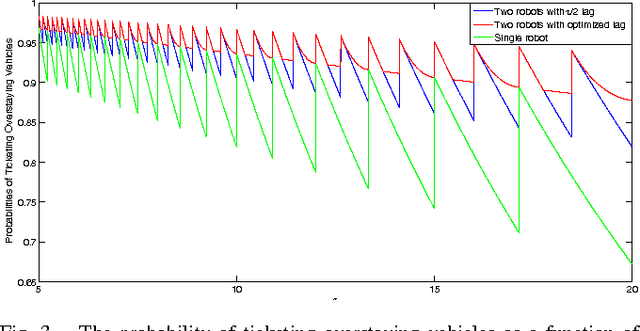
In this paper we consider a robot patrolling problem in which events arrive randomly over time at the vertices of a graph. When an event arrives it remains active for a random amount of time. If that time active exceeds a certain threshold, then we say that the event is a true event; otherwise it is a false event. The robot(s) can traverse the graph to detect newly arrived events, and can revisit these events in order to classify them as true or false. The goal is to plan robot paths that maximize the number of events that are correctly classified, with the constraint that there are no false positives. We show that the offline version of this problem is NP-hard. We then consider a simple patrolling policy based on the traveling salesman tour, and characterize the probability of correctly classifying an event. We investigate the problem when multiple robots follow the same path, and we derive the optimal (and not necessarily uniform) spacing between robots on the path.