RENOIR - A Dataset for Real Low-Light Image Noise Reduction

Image denoising algorithms are evaluated using images corrupted by artificial noise, which may lead to incorrect conclusions about their performances on real noise. In this paper we introduce a dataset of color images corrupted by natural noise due to low-light conditions, together with spatially and intensity-aligned low noise images of the same scenes. We also introduce a method for estimating the true noise level in our images, since even the low noise images contain small amounts of noise. We evaluate the accuracy of our noise estimation method on real and artificial noise, and investigate the Poisson-Gaussian noise model. Finally, we use our dataset to evaluate six denoising algorithms: Active Random Field, BM3D, Bilevel-MRF, Multi-Layer Perceptron, and two versions of NL-means. We show that while the Multi-Layer Perceptron, Bilevel-MRF, and NL-means with soft threshold outperform BM3D on gray images with synthetic noise, they lag behind on our dataset.

Parameterized Principal Component Analysis

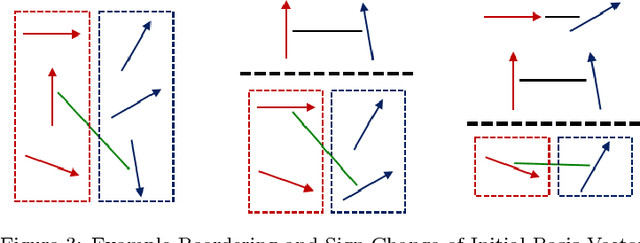
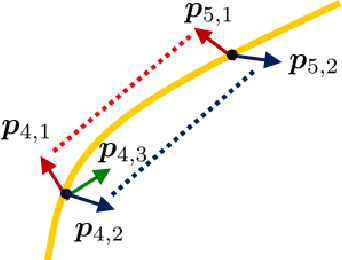
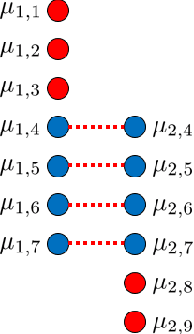
When modeling multivariate data, one might have an extra parameter of contextual information that could be used to treat some observations as more similar to others. For example, images of faces can vary by age, and one would expect the face of a 40 year old to be more similar to the face of a 30 year old than to a baby face. We introduce a novel manifold approximation method, parameterized principal component analysis (PPCA) that models data with linear subspaces that change continuously according to the extra parameter of contextual information (e.g. age), instead of ad-hoc atlases. Special care has been taken in the loss function and the optimization method to encourage smoothly changing subspaces across the parameter values. The approach ensures that each observation's projection will share information with observations that have similar parameter values, but not with observations that have large parameter differences. We tested PPCA on artificial data based on known, smooth functions of an added parameter, as well as on three real datasets with different types of parameters. We compared PPCA to PCA, sparse PCA and to independent principal component analysis (IPCA), which groups observations by their parameter values and projects each group using PCA with no sharing of information for different groups. PPCA recovers the known functions with less error and projects the datasets' test set observations with consistently less reconstruction error than IPCA does. In some cases where the manifold is truly nonlinear, PCA outperforms all the other manifold approximation methods compared.

Feature Selection with Annealing for Computer Vision and Big Data Learning

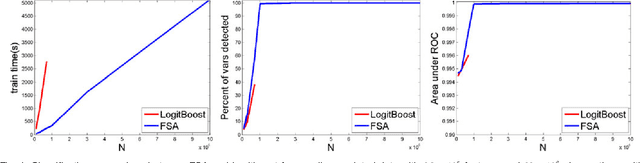
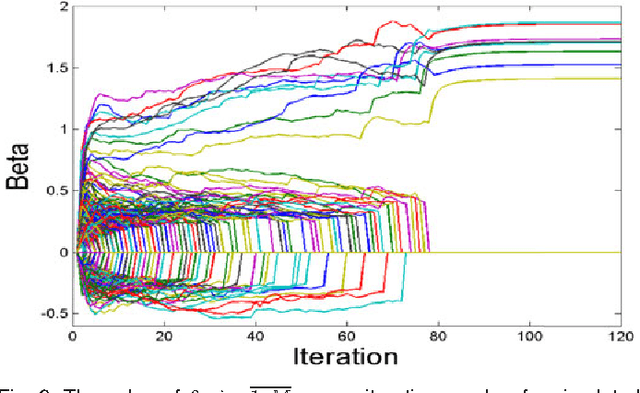
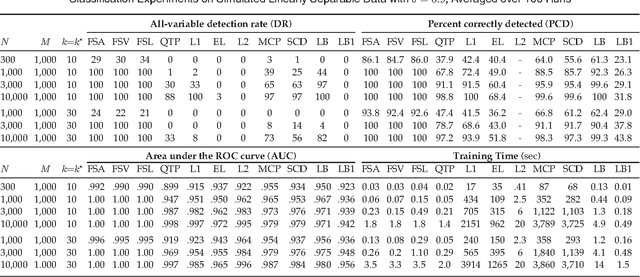
Many computer vision and medical imaging problems are faced with learning from large-scale datasets, with millions of observations and features. In this paper we propose a novel efficient learning scheme that tightens a sparsity constraint by gradually removing variables based on a criterion and a schedule. The attractive fact that the problem size keeps dropping throughout the iterations makes it particularly suitable for big data learning. Our approach applies generically to the optimization of any differentiable loss function, and finds applications in regression, classification and ranking. The resultant algorithms build variable screening into estimation and are extremely simple to implement. We provide theoretical guarantees of convergence and selection consistency. In addition, one dimensional piecewise linear response functions are used to account for nonlinearity and a second order prior is imposed on these functions to avoid overfitting. Experiments on real and synthetic data show that the proposed method compares very well with other state of the art methods in regression, classification and ranking while being computationally very efficient and scalable.

Face Detection with a 3D Model

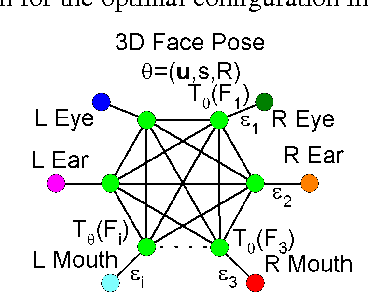
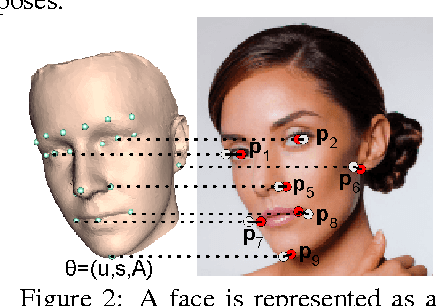
This paper presents a part-based face detection approach where the spatial relationship between the face parts is represented by a hidden 3D model with six parameters. The computational complexity of the search in the six dimensional pose space is addressed by proposing meaningful 3D pose candidates by image-based regression from detected face keypoint locations. The 3D pose candidates are evaluated using a parameter sensitive classifier based on difference features relative to the 3D pose. A compatible subset of candidates is then obtained by non-maximal suppression. Experiments on two standard face detection datasets show that the proposed 3D model based approach obtains results comparable to or better than state of the art.

Learning Mixtures of Bernoulli Templates by Two-Round EM with Performance Guarantee

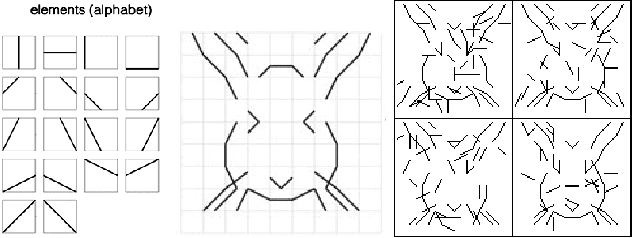
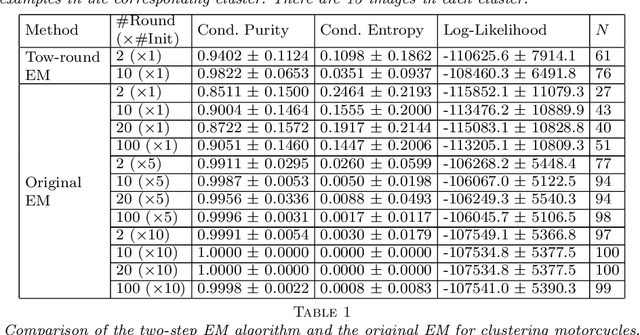
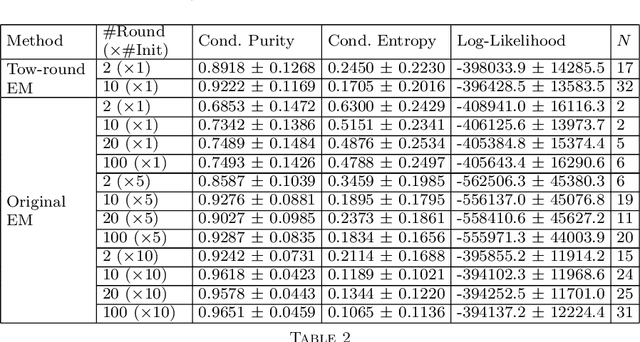
Dasgupta and Shulman showed that a two-round variant of the EM algorithm can learn mixture of Gaussian distributions with near optimal precision with high probability if the Gaussian distributions are well separated and if the dimension is sufficiently high. In this paper, we generalize their theory to learning mixture of high-dimensional Bernoulli templates. Each template is a binary vector, and a template generates examples by randomly switching its binary components independently with a certain probability. In computer vision applications, a binary vector is a feature map of an image, where each binary component indicates whether a local feature or structure is present or absent within a certain cell of the image domain. A Bernoulli template can be considered as a statistical model for images of objects (or parts of objects) from the same category. We show that the two-round EM algorithm can learn mixture of Bernoulli templates with near optimal precision with high probability, if the Bernoulli templates are sufficiently different and if the number of features is sufficiently high. We illustrate the theoretical results by synthetic and real examples.

Hierarchical Object Parsing from Structured Noisy Point Clouds

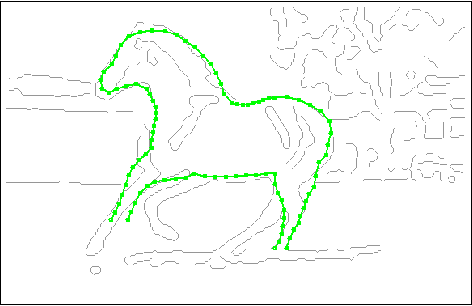
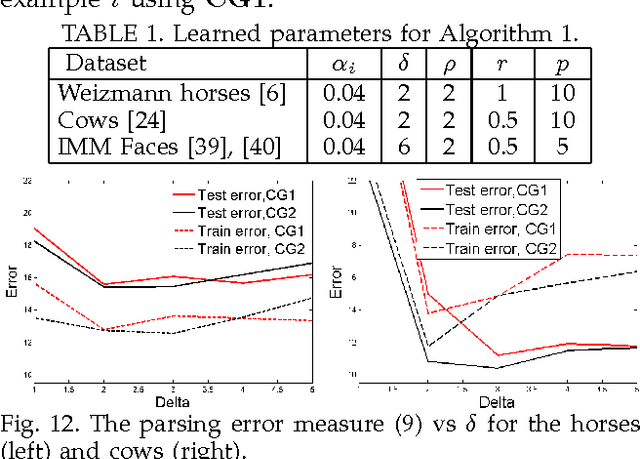
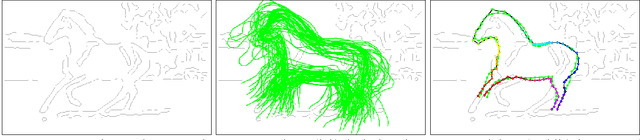
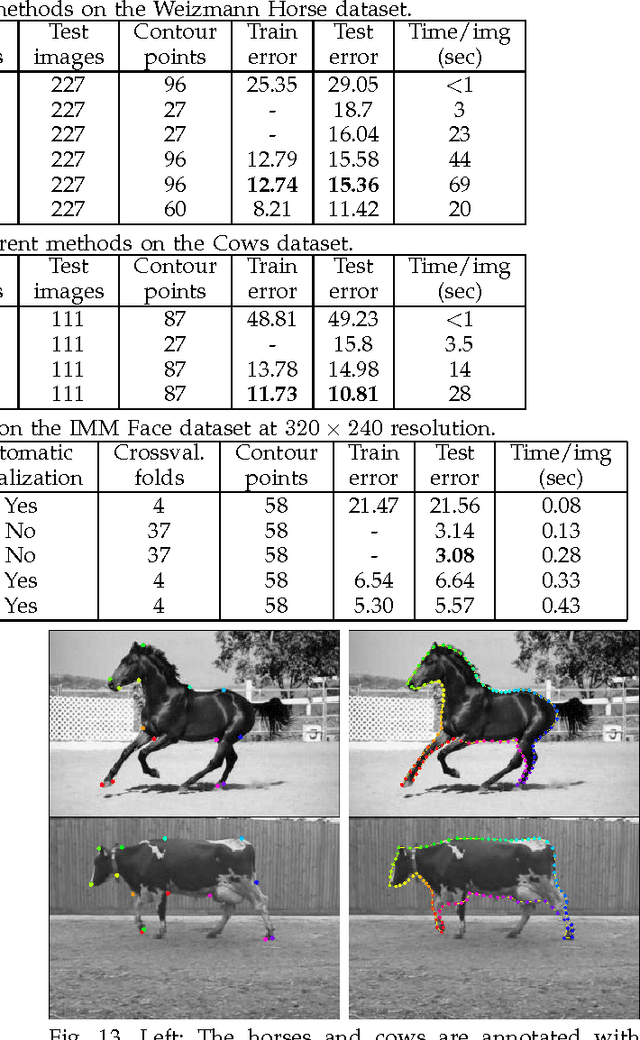
Object parsing and segmentation from point clouds are challenging tasks because the relevant data is available only as thin structures along object boundaries or other features, and is corrupted by large amounts of noise. To handle this kind of data, flexible shape models are desired that can accurately follow the object boundaries. Popular models such as Active Shape and Active Appearance models lack the necessary flexibility for this task, while recent approaches such as the Recursive Compositional Models make model simplifications in order to obtain computational guarantees. This paper investigates a hierarchical Bayesian model of shape and appearance in a generative setting. The input data is explained by an object parsing layer, which is a deformation of a hidden PCA shape model with Gaussian prior. The paper also introduces a novel efficient inference algorithm that uses informed data-driven proposals to initialize local searches for the hidden variables. Applied to the problem of object parsing from structured point clouds such as edge detection images, the proposed approach obtains state of the art parsing errors on two standard datasets without using any intensity information.

An Introduction to Artificial Prediction Markets for Classification

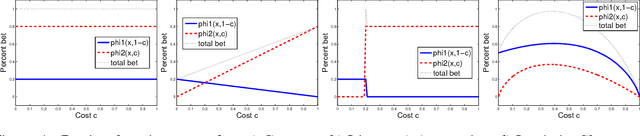
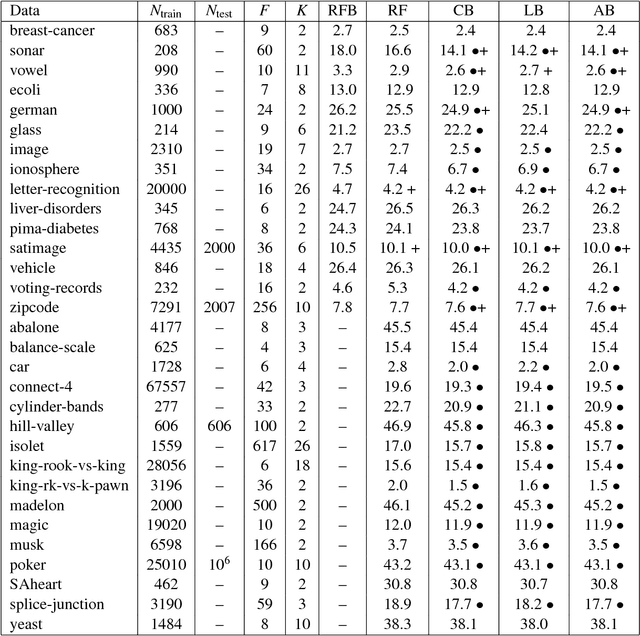
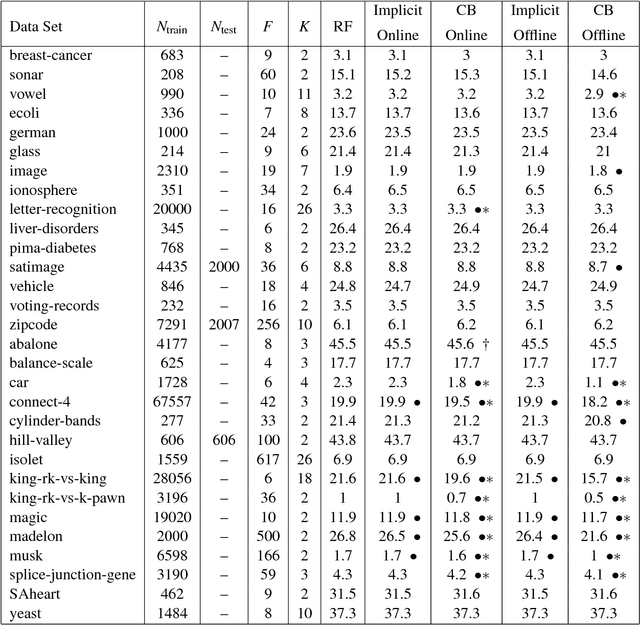
Prediction markets are used in real life to predict outcomes of interest such as presidential elections. This paper presents a mathematical theory of artificial prediction markets for supervised learning of conditional probability estimators. The artificial prediction market is a novel method for fusing the prediction information of features or trained classifiers, where the fusion result is the contract price on the possible outcomes. The market can be trained online by updating the participants' budgets using training examples. Inspired by the real prediction markets, the equations that govern the market are derived from simple and reasonable assumptions. Efficient numerical algorithms are presented for solving these equations. The obtained artificial prediction market is shown to be a maximum likelihood estimator. It generalizes linear aggregation, existent in boosting and random forest, as well as logistic regression and some kernel methods. Furthermore, the market mechanism allows the aggregation of specialized classifiers that participate only on specific instances. Experimental comparisons show that the artificial prediction markets often outperform random forest and implicit online learning on synthetic data and real UCI datasets. Moreover, an extensive evaluation for pelvic and abdominal lymph node detection in CT data shows that the prediction market improves adaboost's detection rate from 79.6% to 81.2% at 3 false positives/volume.

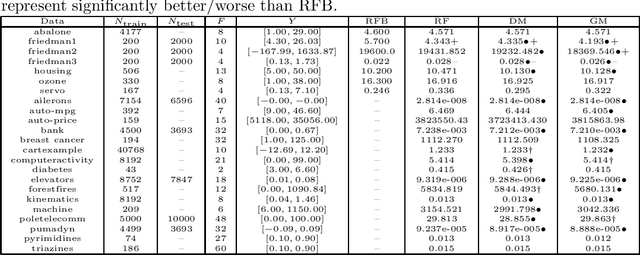
The Artificial Regression Market

The Artificial Prediction Market is a recent machine learning technique for multi-class classification, inspired from the financial markets. It involves a number of trained market participants that bet on the possible outcomes and are rewarded if they predict correctly. This paper generalizes the scope of the Artificial Prediction Markets to regression, where there are uncountably many possible outcomes and the error is usually the MSE. For that, we introduce the reward kernel that rewards each participant based on its prediction error and we derive the price equations. Using two reward kernels we obtain two different learning rules, one of which is approximated using Hermite-Gauss quadrature. The market setting makes it easy to aggregate specialized regressors that only predict when an observation falls into their specialization domain. Experiments show that regression markets based on the two learning rules outperform Random Forest Regression on many UCI datasets and are rarely outperformed.

SPADES and mixture models

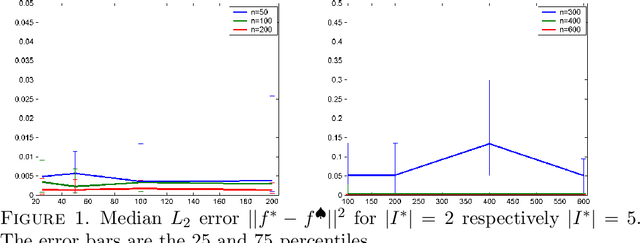
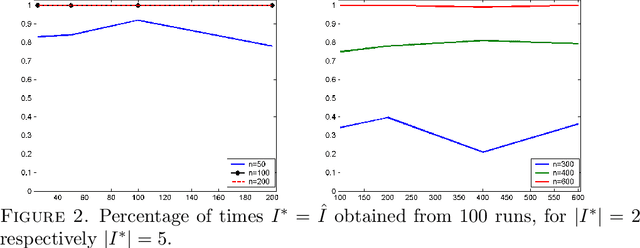
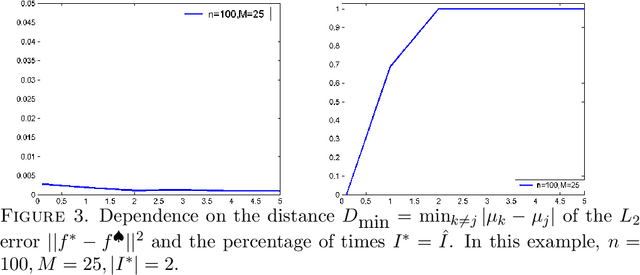
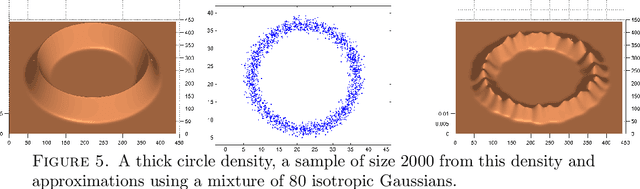
This paper studies sparse density estimation via $\ell_1$ penalization (SPADES). We focus on estimation in high-dimensional mixture models and nonparametric adaptive density estimation. We show, respectively, that SPADES can recover, with high probability, the unknown components of a mixture of probability densities and that it yields minimax adaptive density estimates. These results are based on a general sparsity oracle inequality that the SPADES estimates satisfy. We offer a data driven method for the choice of the tuning parameter used in the construction of SPADES. The method uses the generalized bisection method first introduced in \citebb09. The suggested procedure bypasses the need for a grid search and offers substantial computational savings. We complement our theoretical results with a simulation study that employs this method for approximations of one and two-dimensional densities with mixtures. The numerical results strongly support our theoretical findings.

Dimension reduction and variable selection in case control studies via regularized likelihood optimization

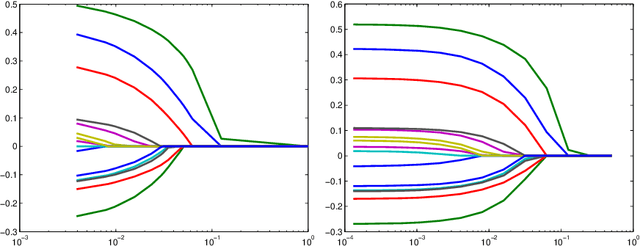
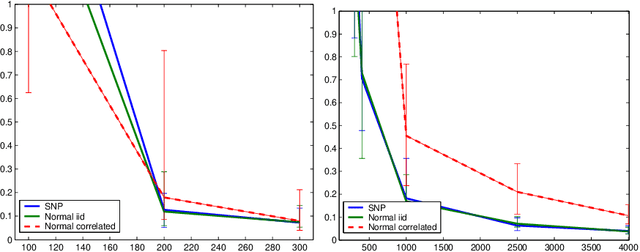
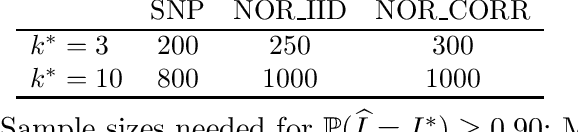
Dimension reduction and variable selection are performed routinely in case-control studies, but the literature on the theoretical aspects of the resulting estimates is scarce. We bring our contribution to this literature by studying estimators obtained via L1 penalized likelihood optimization. We show that the optimizers of the L1 penalized retrospective likelihood coincide with the optimizers of the L1 penalized prospective likelihood. This extends the results of Prentice and Pyke (1979), obtained for non-regularized likelihoods. We establish both the sup-norm consistency of the odds ratio, after model selection, and the consistency of subset selection of our estimators. The novelty of our theoretical results consists in the study of these properties under the case-control sampling scheme. Our results hold for selection performed over a large collection of candidate variables, with cardinality allowed to depend and be greater than the sample size. We complement our theoretical results with a novel approach of determining data driven tuning parameters, based on the bisection method. The resulting procedure offers significant computational savings when compared with grid search based methods. All our numerical experiments support strongly our theoretical findings.