Florentina Bunea
Learning large softmax mixtures with warm start EM
Sep 16, 2024


Abstract:Mixed multinomial logits are discrete mixtures introduced several decades ago to model the probability of choosing an attribute from $p$ possible candidates, in heterogeneous populations. The model has recently attracted attention in the AI literature, under the name softmax mixtures, where it is routinely used in the final layer of a neural network to map a large number $p$ of vectors in $\mathbb{R}^L$ to a probability vector. Despite its wide applicability and empirical success, statistically optimal estimators of the mixture parameters, obtained via algorithms whose running time scales polynomially in $L$, are not known. This paper provides a solution to this problem for contemporary applications, such as large language models, in which the mixture has a large number $p$ of support points, and the size $N$ of the sample observed from the mixture is also large. Our proposed estimator combines two classical estimators, obtained respectively via a method of moments (MoM) and the expectation-minimization (EM) algorithm. Although both estimator types have been studied, from a theoretical perspective, for Gaussian mixtures, no similar results exist for softmax mixtures for either procedure. We develop a new MoM parameter estimator based on latent moment estimation that is tailored to our model, and provide the first theoretical analysis for a MoM-based procedure in softmax mixtures. Although consistent, MoM for softmax mixtures can exhibit poor numerical performance, as observed other mixture models. Nevertheless, as MoM is provably in a neighborhood of the target, it can be used as warm start for any iterative algorithm. We study in detail the EM algorithm, and provide its first theoretical analysis for softmax mixtures. Our final proposal for parameter estimation is the EM algorithm with a MoM warm start.
The Sketched Wasserstein Distance for mixture distributions
Jun 26, 2022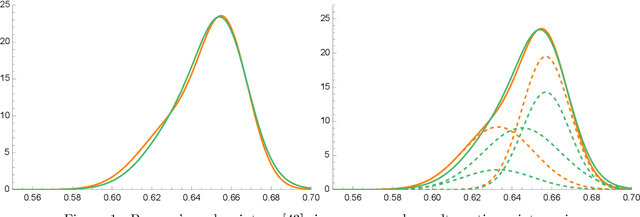

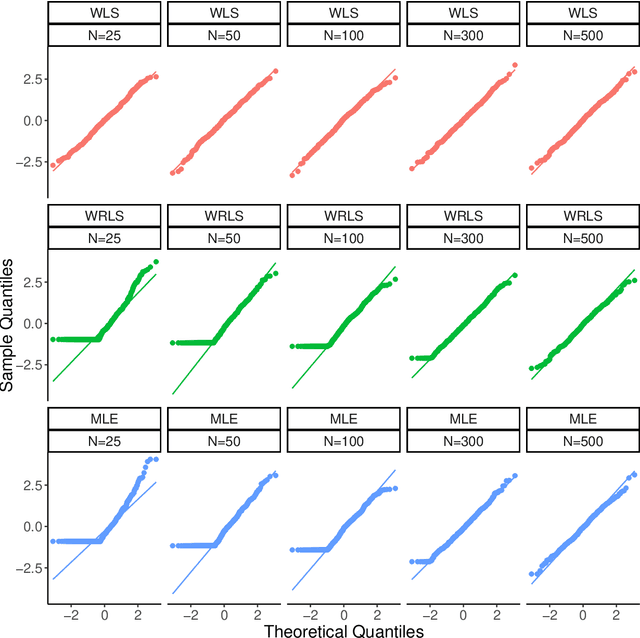
Abstract:The Sketched Wasserstein Distance ($W^S$) is a new probability distance specifically tailored to finite mixture distributions. Given any metric $d$ defined on a set $\mathcal{A}$ of probability distributions, $W^S$ is defined to be the most discriminative convex extension of this metric to the space $\mathcal{S} = \textrm{conv}(\mathcal{A})$ of mixtures of elements of $\mathcal{A}$. Our representation theorem shows that the space $(\mathcal{S}, W^S)$ constructed in this way is isomorphic to a Wasserstein space over $\mathcal{X} = (\mathcal{A}, d)$. This result establishes a universality property for the Wasserstein distances, revealing them to be uniquely characterized by their discriminative power for finite mixtures. We exploit this representation theorem to propose an estimation methodology based on Kantorovich--Rubenstein duality, and prove a general theorem that shows that its estimation error can be bounded by the sum of the errors of estimating the mixture weights and the mixture components, for any estimators of these quantities. We derive sharp statistical properties for the estimated $W^S$ in the case of $p$-dimensional discrete $K$-mixtures, which we show can be estimated at a rate proportional to $\sqrt{K/N}$, up to logarithmic factors. We complement these bounds with a minimax lower bound on the risk of estimating the Wasserstein distance between distributions on a $K$-point metric space, which matches our upper bound up to logarithmic factors. This result is the first nearly tight minimax lower bound for estimating the Wasserstein distance between discrete distributions. Furthermore, we construct $\sqrt{N}$ asymptotically normal estimators of the mixture weights, and derive a $\sqrt{N}$ distributional limit of our estimator of $W^S$ as a consequence. Simulation studies and a data analysis provide strong support on the applicability of the new Sketched Wasserstein Distance.
Likelihood estimation of sparse topic distributions in topic models and its applications to Wasserstein document distance calculations
Jul 12, 2021

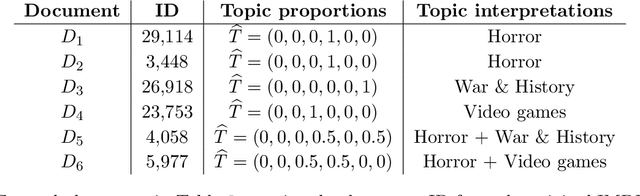
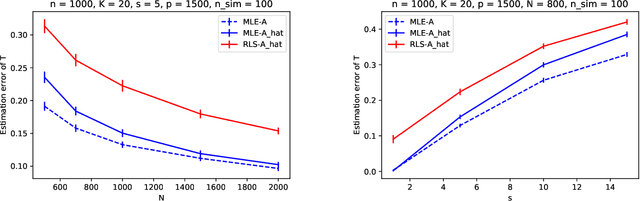
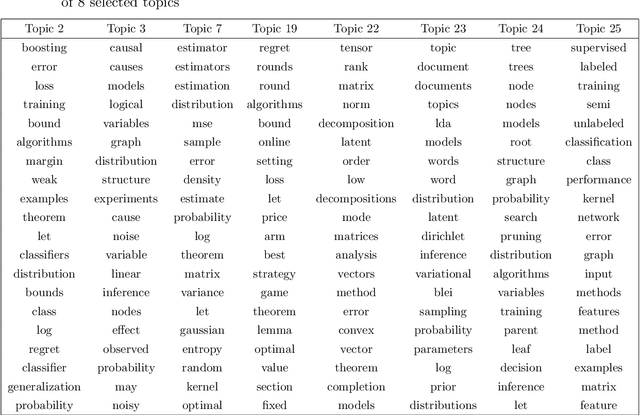
Abstract:This paper studies the estimation of high-dimensional, discrete, possibly sparse, mixture models in topic models. The data consists of observed multinomial counts of $p$ words across $n$ independent documents. In topic models, the $p\times n$ expected word frequency matrix is assumed to be factorized as a $p\times K$ word-topic matrix $A$ and a $K\times n$ topic-document matrix $T$. Since columns of both matrices represent conditional probabilities belonging to probability simplices, columns of $A$ are viewed as $p$-dimensional mixture components that are common to all documents while columns of $T$ are viewed as the $K$-dimensional mixture weights that are document specific and are allowed to be sparse. The main interest is to provide sharp, finite sample, $\ell_1$-norm convergence rates for estimators of the mixture weights $T$ when $A$ is either known or unknown. For known $A$, we suggest MLE estimation of $T$. Our non-standard analysis of the MLE not only establishes its $\ell_1$ convergence rate, but reveals a remarkable property: the MLE, with no extra regularization, can be exactly sparse and contain the true zero pattern of $T$. We further show that the MLE is both minimax optimal and adaptive to the unknown sparsity in a large class of sparse topic distributions. When $A$ is unknown, we estimate $T$ by optimizing the likelihood function corresponding to a plug in, generic, estimator $\hat{A}$ of $A$. For any estimator $\hat{A}$ that satisfies carefully detailed conditions for proximity to $A$, the resulting estimator of $T$ is shown to retain the properties established for the MLE. The ambient dimensions $K$ and $p$ are allowed to grow with the sample sizes. Our application is to the estimation of 1-Wasserstein distances between document generating distributions. We propose, estimate and analyze new 1-Wasserstein distances between two probabilistic document representations.
Prediction in latent factor regression: Adaptive PCR and beyond
Jul 20, 2020
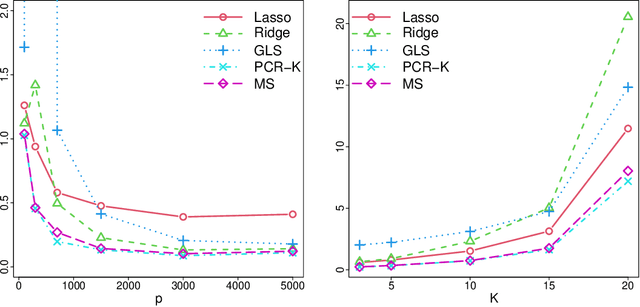
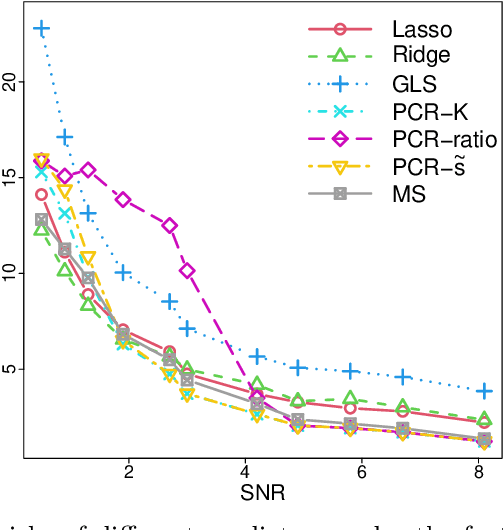
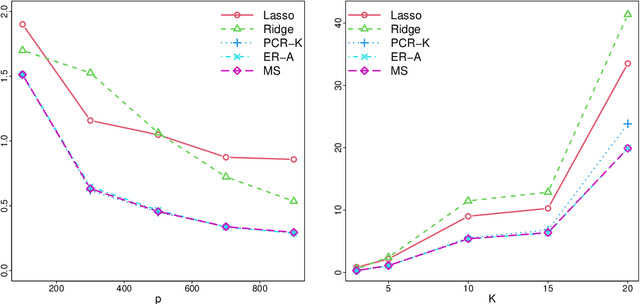
Abstract:This work is devoted to the finite sample prediction risk analysis of a class of linear predictors of a response $Y\in \mathbb{R}$ from a high-dimensional random vector $X\in \mathbb{R}^p$ when $(X,Y)$ follows a latent factor regression model generated by a unobservable latent vector $Z$ of dimension less than $p$. Our primary contribution is in establishing finite sample risk bounds for prediction with the ubiquitous Principal Component Regression (PCR) method, under the factor regression model, with the number of principal components adaptively selected from the data---a form of theoretical guarantee that is surprisingly lacking from the PCR literature. To accomplish this, we prove a master theorem that establishes a risk bound for a large class of predictors, including the PCR predictor as a special case. This approach has the benefit of providing a unified framework for the analysis of a wide range of linear prediction methods, under the factor regression setting. In particular, we use our main theorem to recover known risk bounds for the minimum-norm interpolating predictor, which has received renewed attention in the past two years, and a prediction method tailored to a subclass of factor regression models with identifiable parameters. This model-tailored method can be interpreted as prediction via clusters with latent centers. To address the problem of selecting among a set of candidate predictors, we analyze a simple model selection procedure based on data-splitting, providing an oracle inequality under the factor model to prove that the performance of the selected predictor is close to the optimal candidate. We conclude with a detailed simulation study to support and complement our theoretical results.
Interpolation under latent factor regression models
Mar 13, 2020
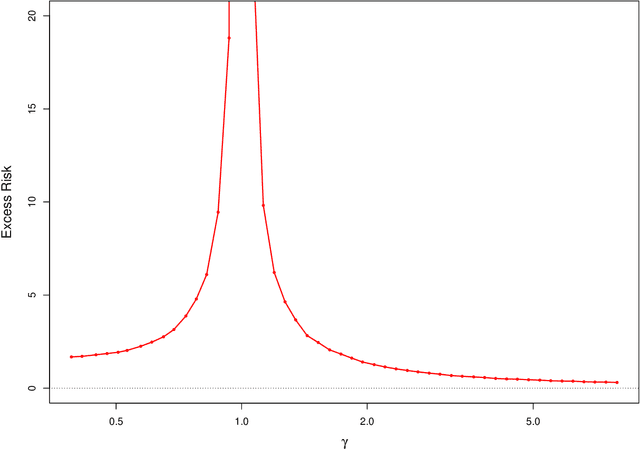
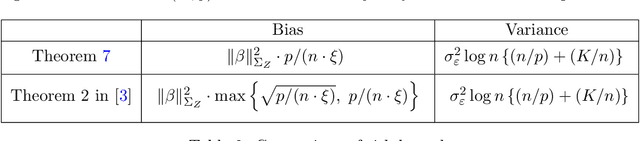
Abstract:This work studies finite-sample properties of the risk of the minimum-norm interpolating predictor in high-dimensional regression models. If the effective rank of the covariance matrix $\Sigma$ of the $p$ regression features is much larger than the sample size $n$, we show that the min-norm interpolating predictor is not desirable, as its risk approaches the risk of trivially predicting the response by $0$. However, our detailed finite sample analysis reveals, surprisingly, that this behavior is not present when the regression response and the features are jointly low-dimensional, and follow a widely used factor regression model. Within this popular model class, and when the effective rank of $\Sigma$ is smaller than $n$, while still allowing for $p \gg n$, both the bias and the variance terms of the excess risk can be controlled, and the risk of the minimum-norm interpolating predictor approaches optimal benchmarks. Moreover, through a detailed analysis of the bias term, we exhibit model classes under which our upper bound on the excess risk approaches zero, while the corresponding upper bound in the recent work arXiv:1906.11300v3 diverges. Furthermore, we show that minimum-norm interpolating predictors analyzed under factor regression models, despite being model-agnostic, can have similar risk to model-assisted predictors based on principal components regression, in the high-dimensional regime.
Optimal estimation of sparse topic models
Jan 22, 2020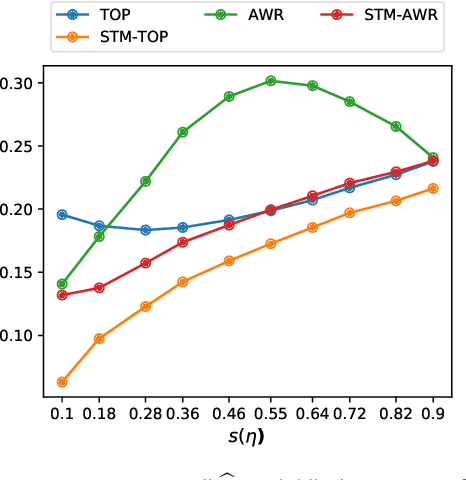
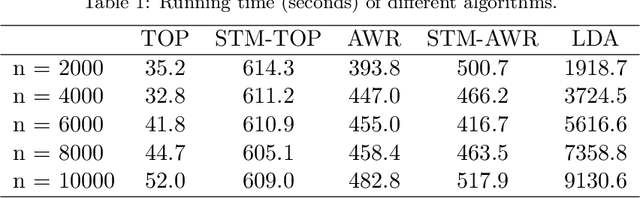
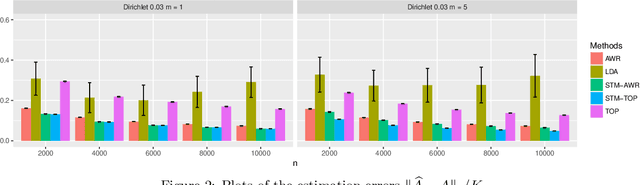
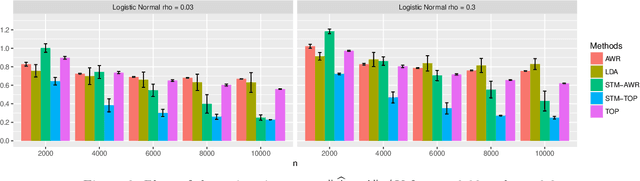
Abstract:Topic models have become popular tools for dimension reduction and exploratory analysis of text data which consists in observed frequencies of a vocabulary of $p$ words in $n$ documents, stored in a $p\times n$ matrix. The main premise is that the mean of this data matrix can be factorized into a product of two non-negative matrices: a $p\times K$ word-topic matrix $A$ and a $K\times n$ topic-document matrix $W$. This paper studies the estimation of $A$ that is possibly element-wise sparse, and the number of topics $K$ is unknown. In this under-explored context, we derive a new minimax lower bound for the estimation of such $A$ and propose a new computationally efficient algorithm for its recovery. We derive a finite sample upper bound for our estimator, and show that it matches the minimax lower bound in many scenarios. Our estimate adapts to the unknown sparsity of $A$ and our analysis is valid for any finite $n$, $p$, $K$ and document lengths. Empirical results on both synthetic data and semi-synthetic data show that our proposed estimator is a strong competitor of the existing state-of-the-art algorithms for both non-sparse $A$ and sparse $A$, and has superior performance is many scenarios of interest.
High-Dimensional Inference for Cluster-Based Graphical Models
Jun 13, 2018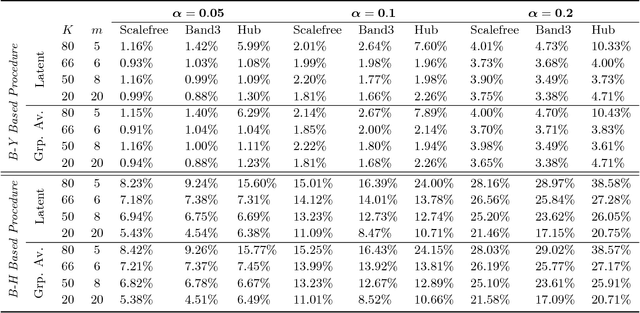
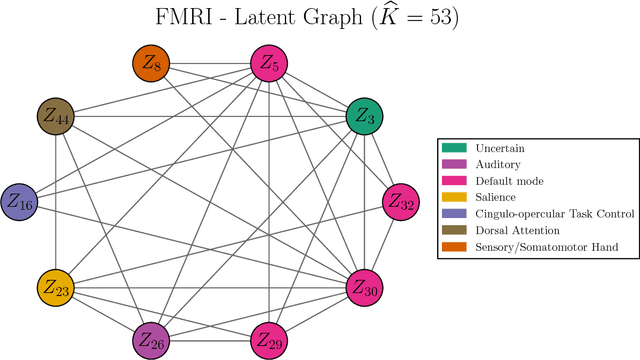
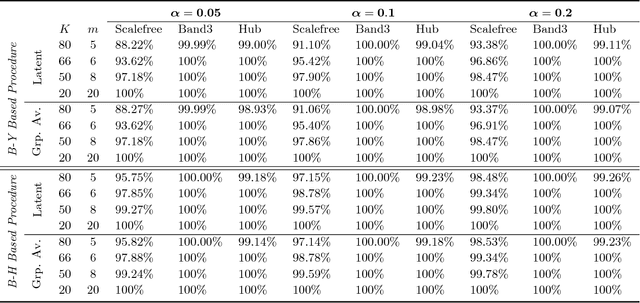
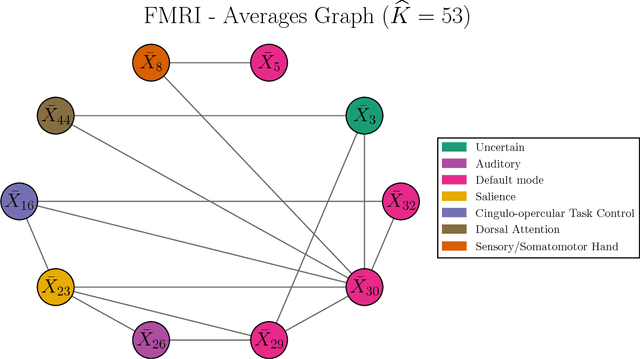
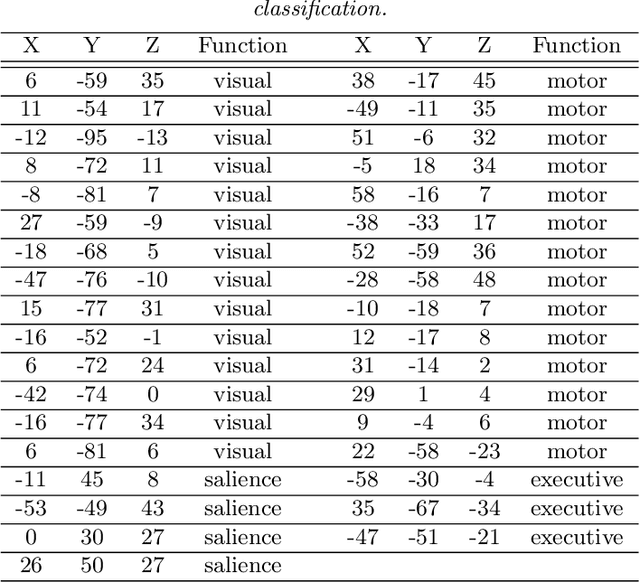
Abstract:Motivated by modern applications in which one constructs graphical models based on a very large number of features, this paper introduces a new class of cluster-based graphical models. Unlike standard graphical models, variable clustering is applied as an initial step for reducing the dimension of the feature space. We employ model assisted clustering, in which the clusters contain features that are similar to the same unobserved latent variable. Two different cluster-based Gaussian graphical models are considered: the latent variable graph, corresponding to the graphical model associated with the unobserved latent variables, and the cluster-average graph, corresponding to the vector of features averaged over clusters. We derive estimates tailored to these graphs, with the goal of pattern recovery under false discovery rate (FDR) control. Our study reveals that likelihood based inference for the latent graph is analytically intractable, and we develop alternative estimation and inference strategies. We replace the likelihood of the data by appropriate empirical risk functions that allow for valid inference in both graphical models under study. Our main results are Berry-Esseen central limit theorems for the proposed estimators, which are proved under weaker assumptions than those employed in the existing literature on Gaussian graphical model inference. We make explicit the implications of the asymptotic approximations on graph recovery under FDR control, and show when it can be controlled asymptotically. Our analysis takes into account the uncertainty induced by the initial clustering step. We find that the errors induced by clustering are asymptotically ignorable in the follow-up analysis, under no further restrictions on the parameter space for which inference is valid. The theoretical properties of the proposed procedures are verified on simulated data and an fMRI data analysis.
A fast algorithm with minimax optimal guarantees for topic models with an unknown number of topics
Jun 12, 2018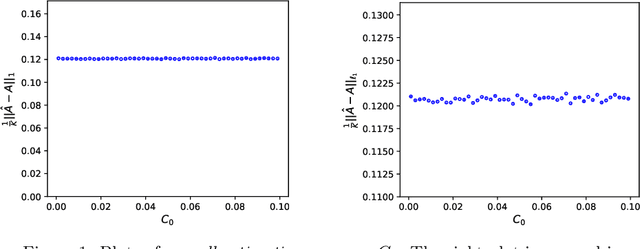

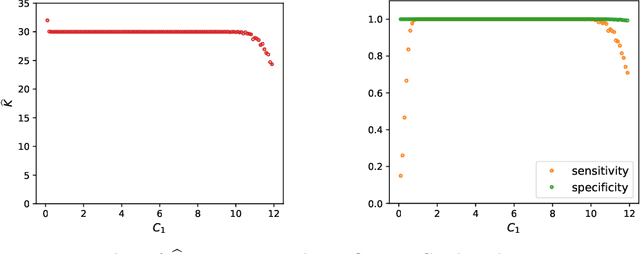
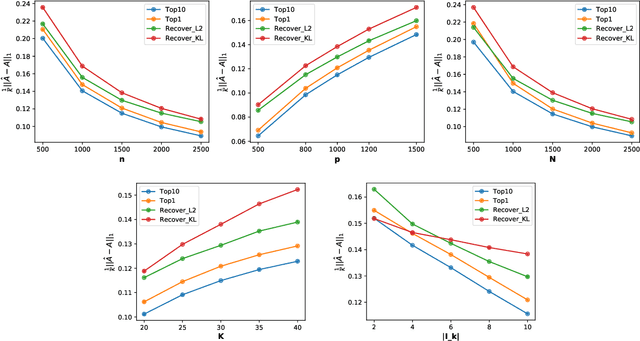
Abstract:We propose a new method of estimation in topic models, that is not a variation on the existing simplex finding algorithms, and that estimates the number of topics K from the observed data. We derive new finite sample minimax lower bounds for the estimation of A, as well as new upper bounds for our proposed estimator. We describe the scenarios where our estimator is minimax adaptive. Our finite sample analysis is valid for any number of documents (n), individual document length (N_i), dictionary size (p) and number of topics (K), and both p and K are allowed to increase with n, a situation not handled well by previous analyses. We complement our theoretical results with a detailed simulation study. We illustrate that the new algorithm is faster and more accurate than the current ones, although we start out with a computational and theoretical disadvantage of not knowing the correct number of topics K, while we provide the competing methods with the correct value in our simulations.
Model Assisted Variable Clustering: Minimax-optimal Recovery and Algorithms
Apr 16, 2018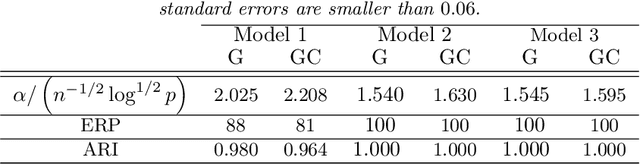
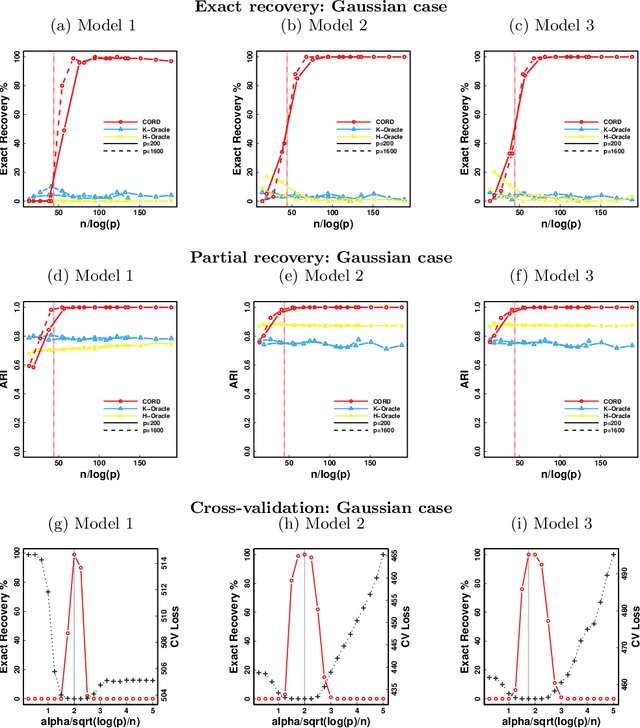
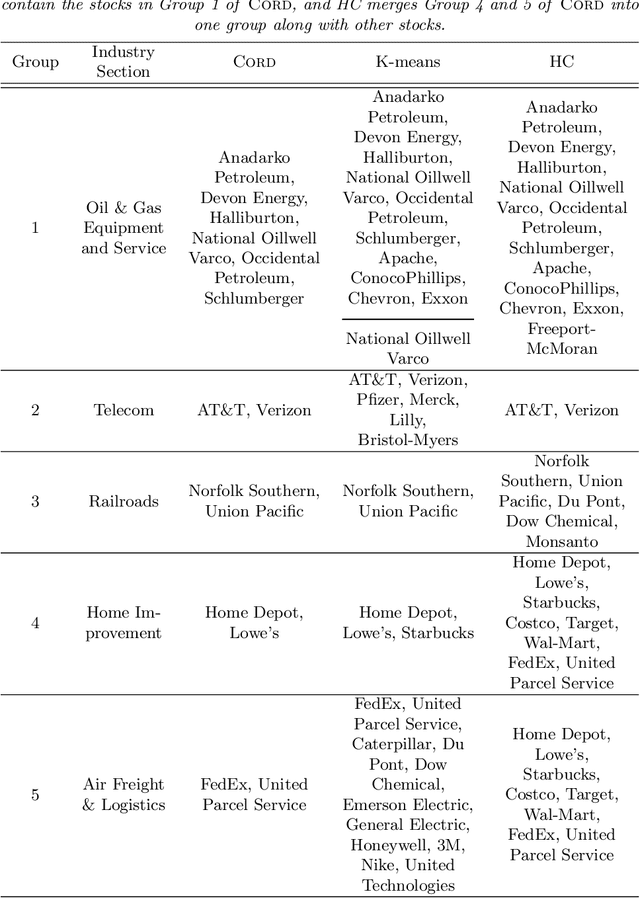
Abstract:Model-based clustering defines population level clusters relative to a model that embeds notions of similarity. Algorithms tailored to such models yield estimated clusters with a clear statistical interpretation. We take this view here and introduce the class of $G$-block covariance models as a background model for variable clustering. In such models, two variables in a cluster are deemed similar if they have similar associations will all other variables. This can arise, for instance, when groups of variables are noise corrupted versions of the same latent factor. We quantify the difficulty of clustering data generated from a $G$-block covariance model in terms of cluster proximity, measured with respect to two related, but different, cluster separation metrics. We derive minimax cluster separation thresholds, which are the metric values below which no algorithm can recover the model-defined clusters exactly, and show that they are different for the two metrics. We therefore develop two algorithms, COD and PECOK, tailored to G-block covariance models, and study their minimax-optimality with respect to each metric. Of independent interest is the fact that the analysis of the PECOK algorithm, which is based on a corrected convex relaxation of the popular $K$-means algorithm, provides the first statistical analysis of such algorithms for variable clustering. Additionally, we contrast our methods with another popular clustering method, spectral clustering, specialized to variable clustering, and show that ensuring exact cluster recovery via this method requires clusters to have a higher separation, relative to the minimax threshold. Extensive simulation studies, as well as our data analyses, confirm the applicability of our approach.
Adaptive Estimation in Structured Factor Models with Applications to Overlapping Clustering
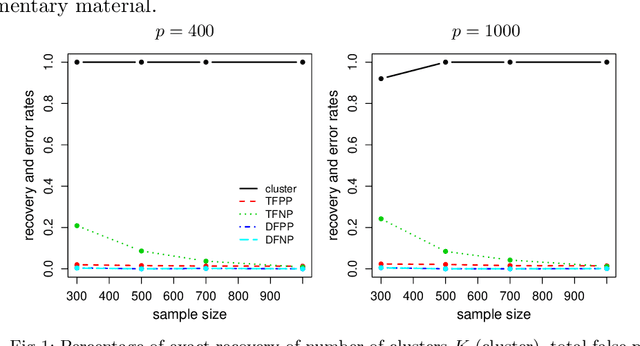
Mar 22, 2018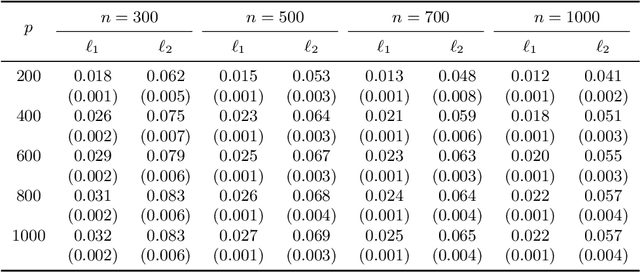
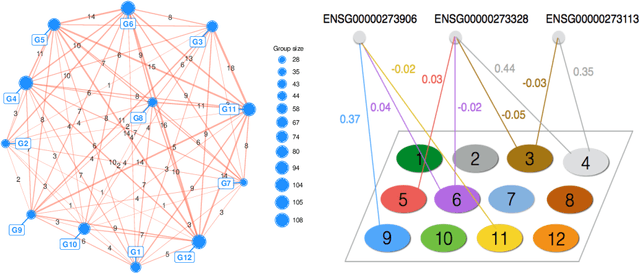
Abstract:This work introduces a novel estimation method, called LOVE, of the entries and structure of a loading matrix A in a sparse latent factor model X = AZ + E, for an observable random vector X in Rp, with correlated unobservable factors Z \in RK, with K unknown, and independent noise E. Each row of A is scaled and sparse. In order to identify the loading matrix A, we require the existence of pure variables, which are components of X that are associated, via A, with one and only one latent factor. Despite the fact that the number of factors K, the number of the pure variables, and their location are all unknown, we only require a mild condition on the covariance matrix of Z, and a minimum of only two pure variables per latent factor to show that A is uniquely defined, up to signed permutations. Our proofs for model identifiability are constructive, and lead to our novel estimation method of the number of factors and of the set of pure variables, from a sample of size n of observations on X. This is the first step of our LOVE algorithm, which is optimization-free, and has low computational complexity of order p2. The second step of LOVE is an easily implementable linear program that estimates A. We prove that the resulting estimator is minimax rate optimal up to logarithmic factors in p. The model structure is motivated by the problem of overlapping variable clustering, ubiquitous in data science. We define the population level clusters as groups of those components of X that are associated, via the sparse matrix A, with the same unobservable latent factor, and multi-factor association is allowed. Clusters are respectively anchored by the pure variables, and form overlapping sub-groups of the p-dimensional random vector X. The Latent model approach to OVErlapping clustering is reflected in the name of our algorithm, LOVE.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge