Localized Multiple Kernel Learning---A Convex Approach

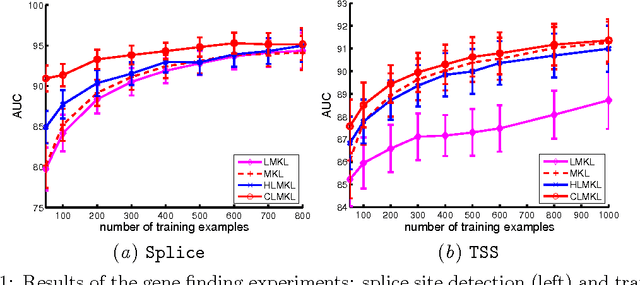
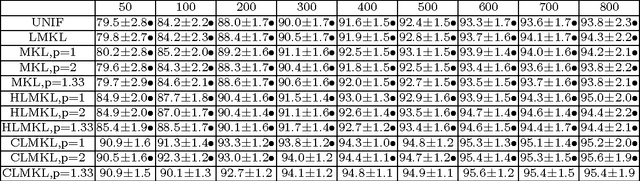
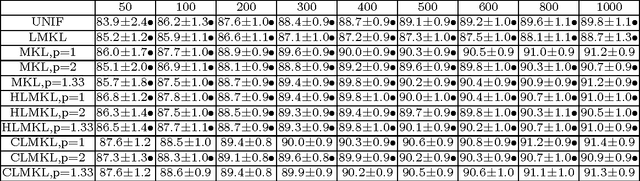
We propose a localized approach to multiple kernel learning that can be formulated as a convex optimization problem over a given cluster structure. For which we obtain generalization error guarantees and derive an optimization algorithm based on the Fenchel dual representation. Experiments on real-world datasets from the application domains of computational biology and computer vision show that convex localized multiple kernel learning can achieve higher prediction accuracies than its global and non-convex local counterparts.

Extensions of stability selection using subsamples of observations and covariates

We introduce extensions of stability selection, a method to stabilise variable selection methods introduced by Meinshausen and B\"uhlmann (J R Stat Soc 72:417-473, 2010). We propose to apply a base selection method repeatedly to random observation subsamples and covariate subsets under scrutiny, and to select covariates based on their selection frequency. We analyse the effects and benefits of these extensions. Our analysis generalizes the theoretical results of Meinshausen and B\"uhlmann (J R Stat Soc 72:417-473, 2010) from the case of half-samples to subsamples of arbitrary size. We study, in a theoretical manner, the effect of taking random covariate subsets using a simplified score model. Finally we validate these extensions on numerical experiments on both synthetic and real datasets, and compare the obtained results in detail to the original stability selection method.

Multi-class SVMs: From Tighter Data-Dependent Generalization Bounds to Novel Algorithms

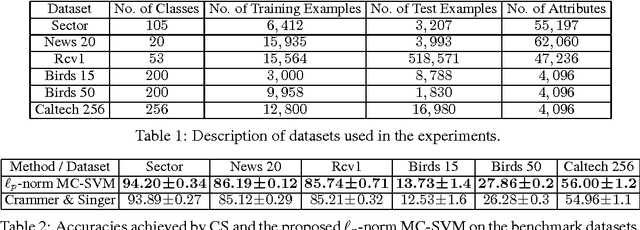
This paper studies the generalization performance of multi-class classification algorithms, for which we obtain, for the first time, a data-dependent generalization error bound with a logarithmic dependence on the class size, substantially improving the state-of-the-art linear dependence in the existing data-dependent generalization analysis. The theoretical analysis motivates us to introduce a new multi-class classification machine based on $\ell_p$-norm regularization, where the parameter $p$ controls the complexity of the corresponding bounds. We derive an efficient optimization algorithm based on Fenchel duality theory. Benchmarks on several real-world datasets show that the proposed algorithm can achieve significant accuracy gains over the state of the art.

Coordinate Descent with Online Adaptation of Coordinate Frequencies

Coordinate descent (CD) algorithms have become the method of choice for solving a number of optimization problems in machine learning. They are particularly popular for training linear models, including linear support vector machine classification, LASSO regression, and logistic regression. We consider general CD with non-uniform selection of coordinates. Instead of fixing selection frequencies beforehand we propose an online adaptation mechanism for this important parameter, called the adaptive coordinate frequencies (ACF) method. This mechanism removes the need to estimate optimal coordinate frequencies beforehand, and it automatically reacts to changing requirements during an optimization run. We demonstrate the usefulness of our ACF-CD approach for a variety of optimization problems arising in machine learning contexts. Our algorithm offers significant speed-ups over state-of-the-art training methods.

Accelerated Linear SVM Training with Adaptive Variable Selection Frequencies

Support vector machine (SVM) training is an active research area since the dawn of the method. In recent years there has been increasing interest in specialized solvers for the important case of linear models. The algorithm presented by Hsieh et al., probably best known under the name of the "liblinear" implementation, marks a major breakthrough. The method is analog to established dual decomposition algorithms for training of non-linear SVMs, but with greatly reduced computational complexity per update step. This comes at the cost of not keeping track of the gradient of the objective any more, which excludes the application of highly developed working set selection algorithms. We present an algorithmic improvement to this method. We replace uniform working set selection with an online adaptation of selection frequencies. The adaptation criterion is inspired by modern second order working set selection methods. The same mechanism replaces the shrinking heuristic. This novel technique speeds up training in some cases by more than an order of magnitude.