PeSANet: Physics-encoded Spectral Attention Network for Simulating PDE-Governed Complex Systems
Paper and Code
May 03, 2025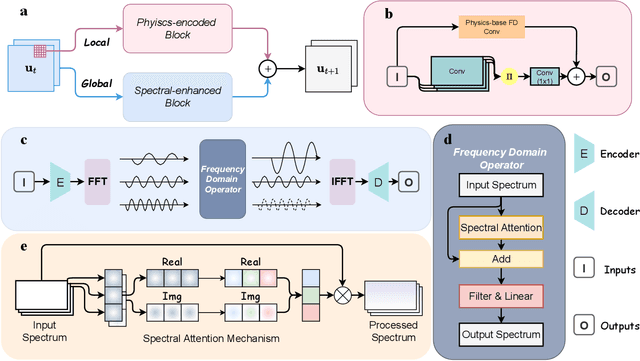

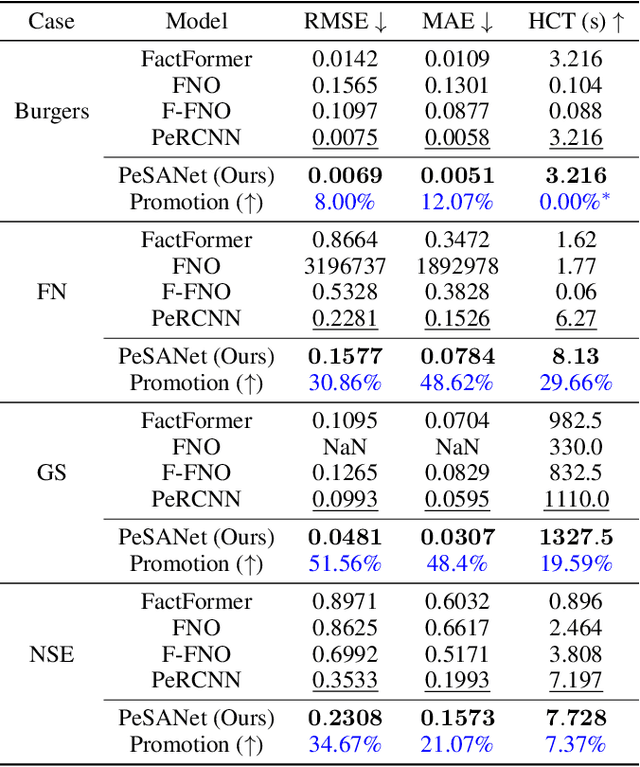
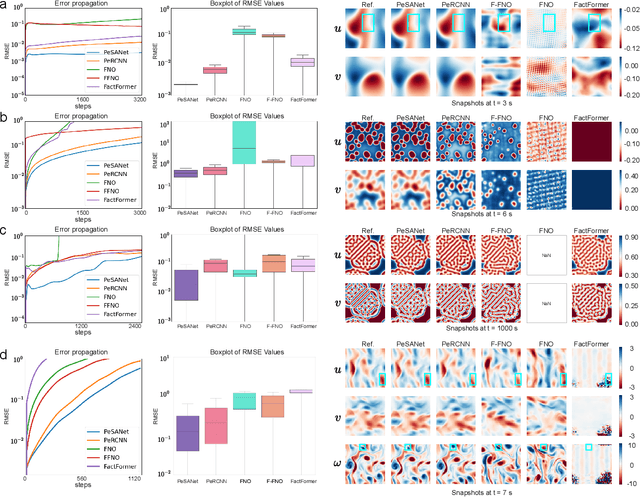
Accurately modeling and forecasting complex systems governed by partial differential equations (PDEs) is crucial in various scientific and engineering domains. However, traditional numerical methods struggle in real-world scenarios due to incomplete or unknown physical laws. Meanwhile, machine learning approaches often fail to generalize effectively when faced with scarce observational data and the challenge of capturing local and global features. To this end, we propose the Physics-encoded Spectral Attention Network (PeSANet), which integrates local and global information to forecast complex systems with limited data and incomplete physical priors. The model consists of two key components: a physics-encoded block that uses hard constraints to approximate local differential operators from limited data, and a spectral-enhanced block that captures long-range global dependencies in the frequency domain. Specifically, we introduce a novel spectral attention mechanism to model inter-spectrum relationships and learn long-range spatial features. Experimental results demonstrate that PeSANet outperforms existing methods across all metrics, particularly in long-term forecasting accuracy, providing a promising solution for simulating complex systems with limited data and incomplete physics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge