Learning Scalable $\ell_\infty$-constrained Near-lossless Image Compression via Joint Lossy Image and Residual Compression
Paper and Code
Mar 31, 2021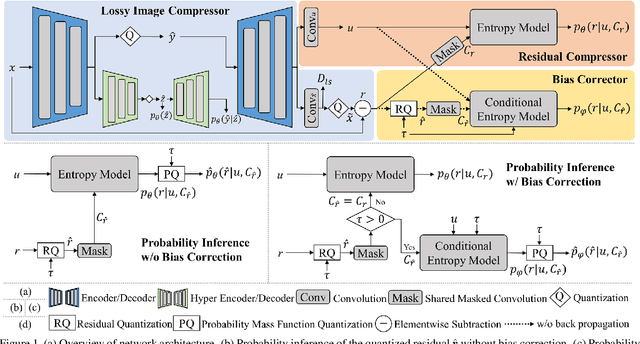
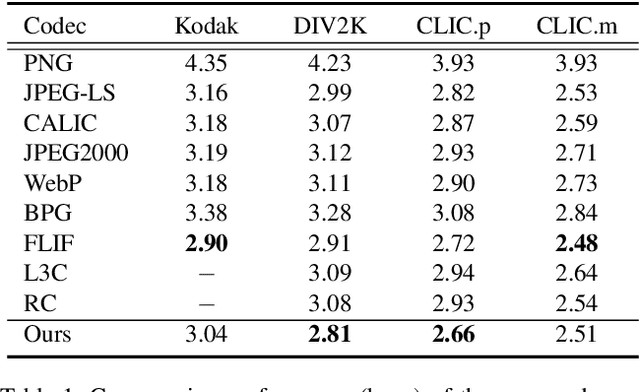
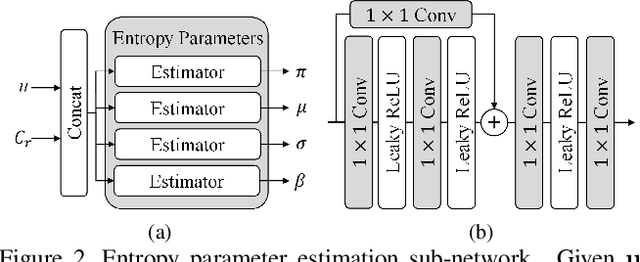
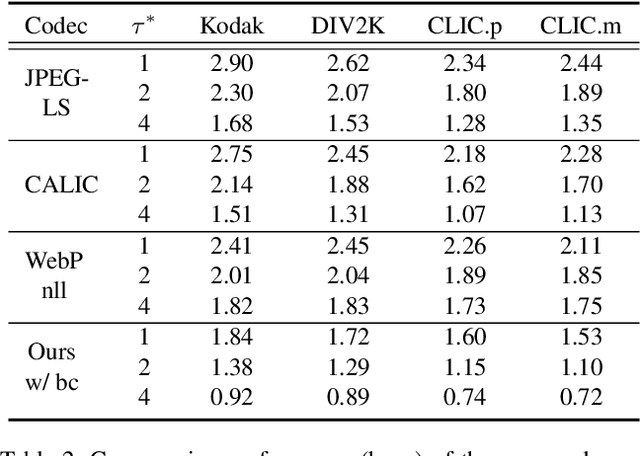
We propose a novel joint lossy image and residual compression framework for learning $\ell_\infty$-constrained near-lossless image compression. Specifically, we obtain a lossy reconstruction of the raw image through lossy image compression and uniformly quantize the corresponding residual to satisfy a given tight $\ell_\infty$ error bound. Suppose that the error bound is zero, i.e., lossless image compression, we formulate the joint optimization problem of compressing both the lossy image and the original residual in terms of variational auto-encoders and solve it with end-to-end training. To achieve scalable compression with the error bound larger than zero, we derive the probability model of the quantized residual by quantizing the learned probability model of the original residual, instead of training multiple networks. We further correct the bias of the derived probability model caused by the context mismatch between training and inference. Finally, the quantized residual is encoded according to the bias-corrected probability model and is concatenated with the bitstream of the compressed lossy image. Experimental results demonstrate that our near-lossless codec achieves the state-of-the-art performance for lossless and near-lossless image compression, and achieves competitive PSNR while much smaller $\ell_\infty$ error compared with lossy image codecs at high bit rates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge