A Hamilton-Jacobi Reachability-Based Framework for Predicting and Analyzing Human Motion for Safe Planning

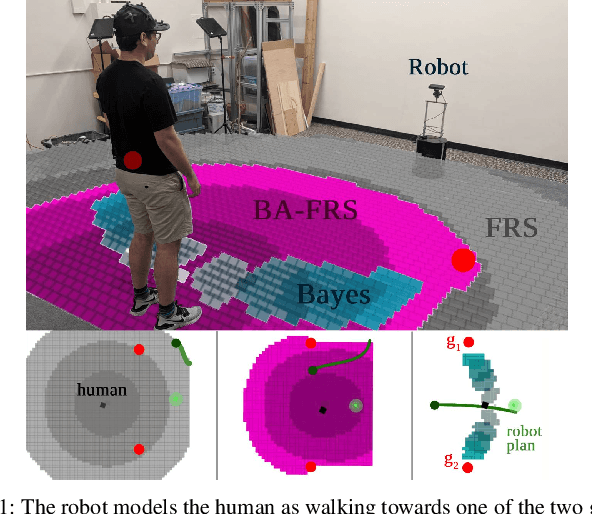
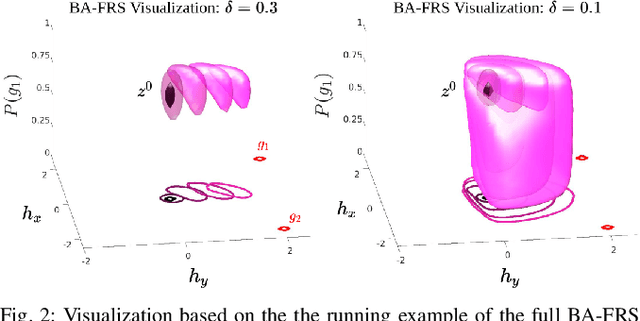
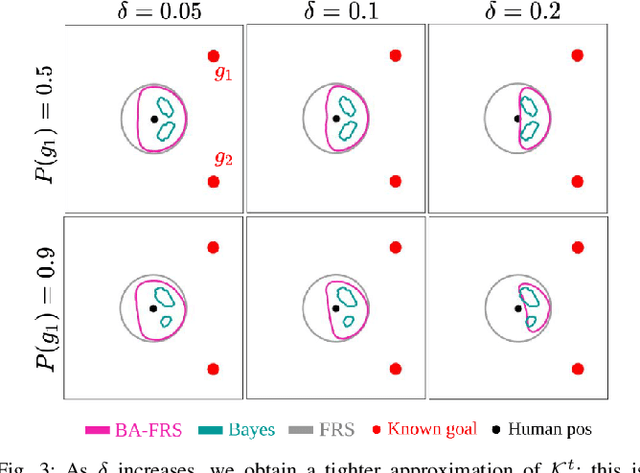
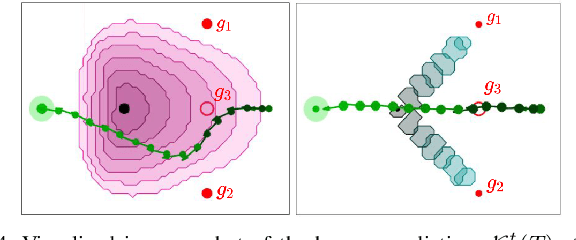
Real-world autonomous systems often employ probabilistic predictive models of human behavior during planning to reason about their future motion. Since accurately modeling the human behavior a priori is challenging, such models are often parameterized, enabling the robot to adapt predictions based on observations by maintaining a distribution over the model parameters. This leads to a probabilistic prediction problem, which even though attractive, can be computationally demanding. In this work, we formalize the prediction problem as a stochastic reachability problem in the joint state space of the human and the belief over the model parameters. We further introduce a Hamilton-Jacobi reachability framework which casts a deterministic approximation of this stochastic reachability problem by restricting the allowable actions to a set rather than a distribution, while still maintaining the belief as an explicit state. This leads to two advantages: our approach gives rise to a novel predictor wherein the predictions can be performed at a significantly lower computational expense, and to a general framework which also enables us to perform predictor analysis. We compare our approach to a fully stochastic predictor using Bayesian inference and the worst-case forward reachable set in simulation and in hardware, and demonstrate how it can enable robust planning while not being overly conservative, even when the human model is inaccurate.