Attention is a smoothed cubic spline

We highlight a perhaps important but hitherto unobserved insight: The attention module in a transformer is a smoothed cubic spline. Viewed in this manner, this mysterious but critical component of a transformer becomes a natural development of an old notion deeply entrenched in classical approximation theory. More precisely, we show that with ReLU-activation, attention, masked attention, encoder-decoder attention are all cubic splines. As every component in a transformer is constructed out of compositions of various attention modules (= cubic splines) and feed forward neural networks (= linear splines), all its components -- encoder, decoder, and encoder-decoder blocks; multilayered encoders and decoders; the transformer itself -- are cubic or higher-order splines. If we assume the Pierce-Birkhoff conjecture, then the converse also holds, i.e., every spline is a ReLU-activated encoder. Since a spline is generally just $C^2$, one way to obtain a smoothed $C^\infty$-version is by replacing ReLU with a smooth activation; and if this activation is chosen to be SoftMax, we recover the original transformer as proposed by Vaswani et al. This insight sheds light on the nature of the transformer by casting it entirely in terms of splines, one of the best known and thoroughly understood objects in applied mathematics.

Online Statistical Inference for Contextual Bandits via Stochastic Gradient Descent

With the fast development of big data, it has been easier than before to learn the optimal decision rule by updating the decision rule recursively and making online decisions. We study the online statistical inference of model parameters in a contextual bandit framework of sequential decision-making. We propose a general framework for online and adaptive data collection environment that can update decision rules via weighted stochastic gradient descent. We allow different weighting schemes of the stochastic gradient and establish the asymptotic normality of the parameter estimator. Our proposed estimator significantly improves the asymptotic efficiency over the previous averaged SGD approach via inverse probability weights. We also conduct an optimality analysis on the weights in a linear regression setting. We provide a Bahadur representation of the proposed estimator and show that the remainder term in the Bahadur representation entails a slower convergence rate compared to classical SGD due to the adaptive data collection.

Stochastic Steffensen method

Is it possible for a first-order method, i.e., only first derivatives allowed, to be quadratically convergent? For univariate loss functions, the answer is yes -- the Steffensen method avoids second derivatives and is still quadratically convergent like Newton method. By incorporating an optimal step size we can even push its convergence order beyond quadratic to $1+\sqrt{2} \approx 2.414$. While such high convergence orders are a pointless overkill for a deterministic algorithm, they become rewarding when the algorithm is randomized for problems of massive sizes, as randomization invariably compromises convergence speed. We will introduce two adaptive learning rates inspired by the Steffensen method, intended for use in a stochastic optimization setting and requires no hyperparameter tuning aside from batch size. Extensive experiments show that they compare favorably with several existing first-order methods. When restricted to a quadratic objective, our stochastic Steffensen methods reduce to randomized Kaczmarz method -- note that this is not true for SGD or SLBFGS -- and thus we may also view our methods as a generalization of randomized Kaczmarz to arbitrary objectives.

Online Statistical Inference for Gradient-free Stochastic Optimization

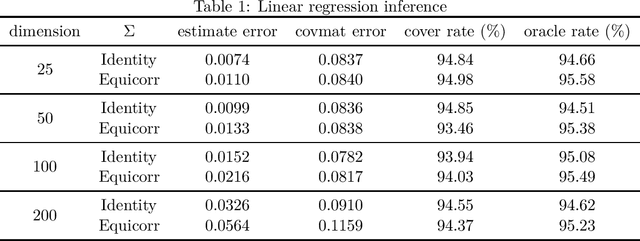
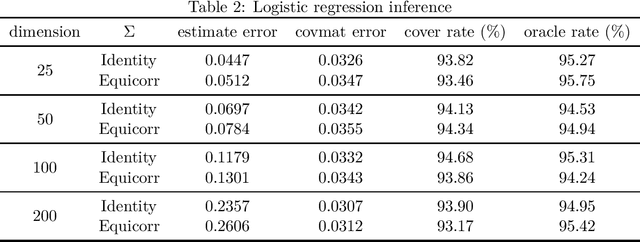
As gradient-free stochastic optimization gains emerging attention for a wide range of applications recently, the demand for uncertainty quantification of parameters obtained from such approaches arises. In this paper, we investigate the problem of statistical inference for model parameters based on gradient-free stochastic optimization methods that use only function values rather than gradients. We first present central limit theorem results for Polyak-Ruppert-averaging type gradient-free estimators. The asymptotic distribution reflects the trade-off between the rate of convergence and function query complexity. We next construct valid confidence intervals for model parameters through the estimation of the covariance matrix in a fully online fashion. We further give a general gradient-free framework for covariance estimation and analyze the role of function query complexity in the convergence rate of the covariance estimator. This provides a one-pass computationally efficient procedure for simultaneously obtaining an estimator of model parameters and conducting statistical inference. Finally, we provide numerical experiments to verify our theoretical results and illustrate some extensions of our method for various machine learning and deep learning applications.

Recht-Ré Noncommutative Arithmetic-Geometric Mean Conjecture is False

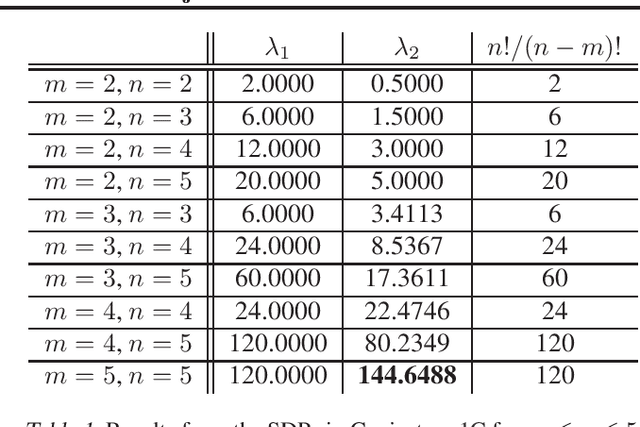
Stochastic optimization algorithms have become indispensable in modern machine learning. An unresolved foundational question in this area is the difference between with-replacement sampling and without-replacement sampling -- does the latter have superior convergence rate compared to the former? A groundbreaking result of Recht and R\'e reduces the problem to a noncommutative analogue of the arithmetic-geometric mean inequality where $n$ positive numbers are replaced by $n$ positive definite matrices. If this inequality holds for all $n$, then without-replacement sampling indeed outperforms with-replacement sampling. The conjectured Recht-R\'e inequality has so far only been established for $n = 2$ and a special case of $n = 3$. We will show that the Recht-R\'e conjecture is false for general $n$. Our approach relies on the noncommutative Positivstellensatz, which allows us to reduce the conjectured inequality to a semidefinite program and the validity of the conjecture to certain bounds for the optimum values, which we show are false as soon as $n = 5$.