Stability and Performance Limits of Adaptive Primal-Dual Networks

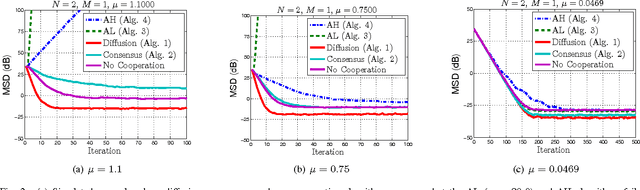
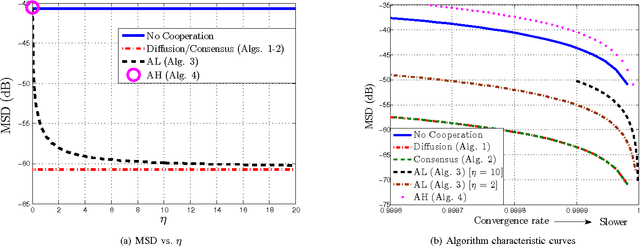
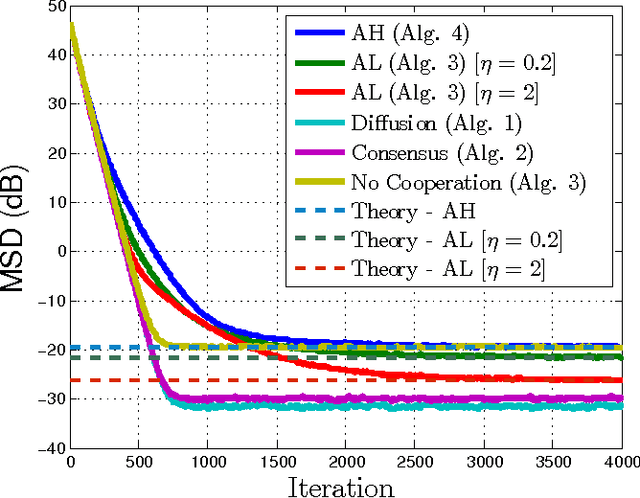
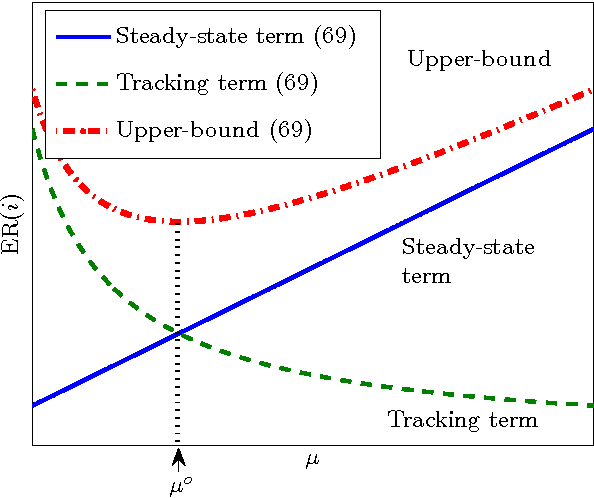
This work studies distributed primal-dual strategies for adaptation and learning over networks from streaming data. Two first-order methods are considered based on the Arrow-Hurwicz (AH) and augmented Lagrangian (AL) techniques. Several revealing results are discovered in relation to the performance and stability of these strategies when employed over adaptive networks. The conclusions establish that the advantages that these methods have for deterministic optimization problems do not necessarily carry over to stochastic optimization problems. It is found that they have narrower stability ranges and worse steady-state mean-square-error performance than primal methods of the consensus and diffusion type. It is also found that the AH technique can become unstable under a partial observation model, while the other techniques are able to recover the unknown under this scenario. A method to enhance the performance of AL strategies is proposed by tying the selection of the step-size to their regularization parameter. It is shown that this method allows the AL algorithm to approach the performance of consensus and diffusion strategies but that it remains less stable than these other strategies.

Dictionary Learning over Distributed Models

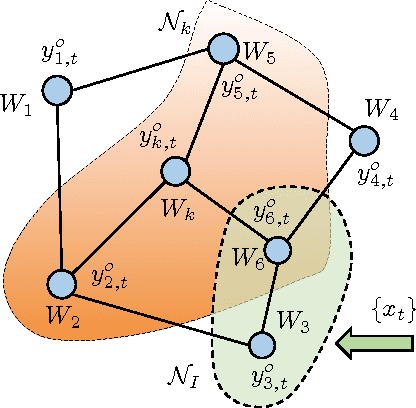
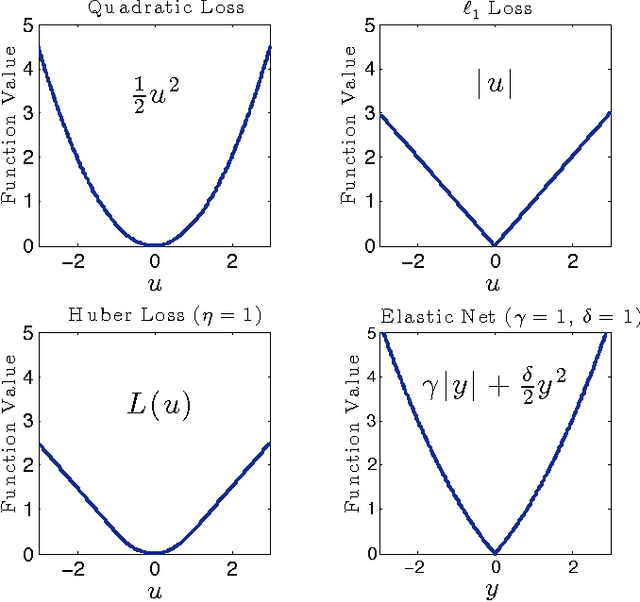
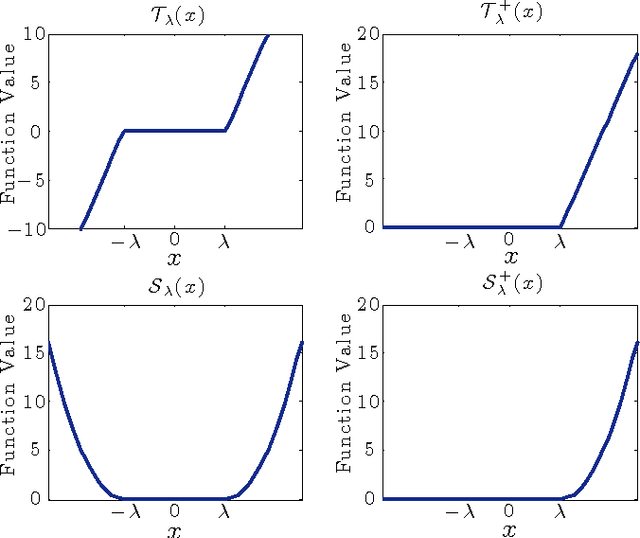
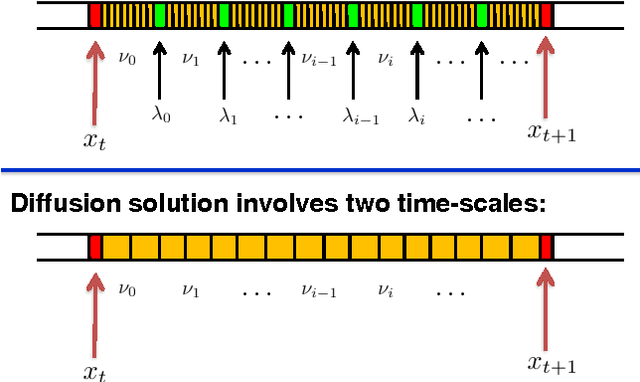
In this paper, we consider learning dictionary models over a network of agents, where each agent is only in charge of a portion of the dictionary elements. This formulation is relevant in Big Data scenarios where large dictionary models may be spread over different spatial locations and it is not feasible to aggregate all dictionaries in one location due to communication and privacy considerations. We first show that the dual function of the inference problem is an aggregation of individual cost functions associated with different agents, which can then be minimized efficiently by means of diffusion strategies. The collaborative inference step generates dual variables that are used by the agents to update their dictionaries without the need to share these dictionaries or even the coefficient models for the training data. This is a powerful property that leads to an effective distributed procedure for learning dictionaries over large networks (e.g., hundreds of agents in our experiments). Furthermore, the proposed learning strategy operates in an online manner and is able to respond to streaming data, where each data sample is presented to the network once.

A Neuron as a Signal Processing Device

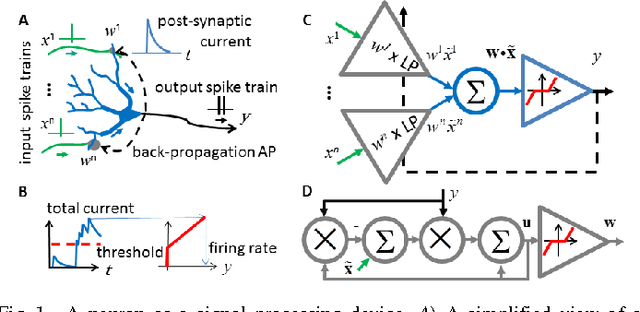
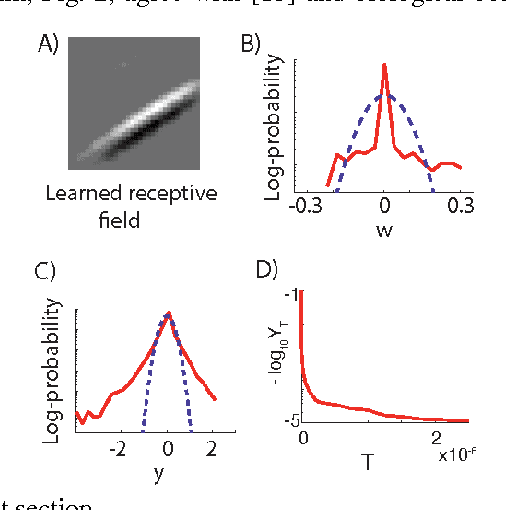
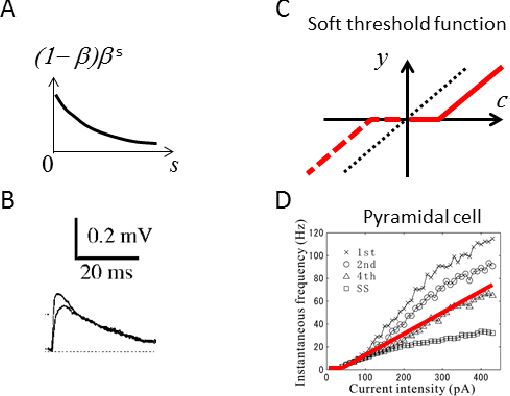
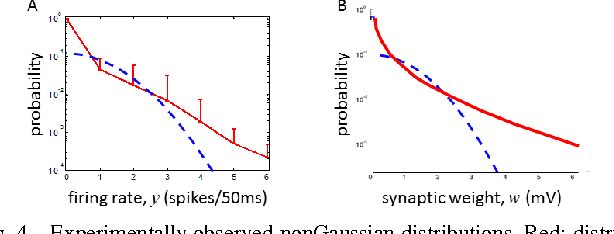
A neuron is a basic physiological and computational unit of the brain. While much is known about the physiological properties of a neuron, its computational role is poorly understood. Here we propose to view a neuron as a signal processing device that represents the incoming streaming data matrix as a sparse vector of synaptic weights scaled by an outgoing sparse activity vector. Formally, a neuron minimizes a cost function comprising a cumulative squared representation error and regularization terms. We derive an online algorithm that minimizes such cost function by alternating between the minimization with respect to activity and with respect to synaptic weights. The steps of this algorithm reproduce well-known physiological properties of a neuron, such as weighted summation and leaky integration of synaptic inputs, as well as an Oja-like, but parameter-free, synaptic learning rule. Our theoretical framework makes several predictions, some of which can be verified by the existing data, others require further experiments. Such framework should allow modeling the function of neuronal circuits without necessarily measuring all the microscopic biophysical parameters, as well as facilitate the design of neuromorphic electronics.

On Distributed Online Classification in the Midst of Concept Drifts

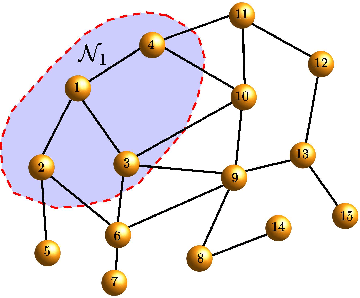
In this work, we analyze the generalization ability of distributed online learning algorithms under stationary and non-stationary environments. We derive bounds for the excess-risk attained by each node in a connected network of learners and study the performance advantage that diffusion strategies have over individual non-cooperative processing. We conduct extensive simulations to illustrate the results.