Deterministic Apple Tasting

In binary ($0/1$) online classification with apple tasting feedback, the learner receives feedback only when predicting $1$. Besides some degenerate learning tasks, all previously known learning algorithms for this model are randomized. Consequently, prior to this work it was unknown whether deterministic apple tasting is generally feasible. In this work, we provide the first widely-applicable deterministic apple tasting learner, and show that in the realizable case, a hypothesis class is learnable if and only if it is deterministically learnable, confirming a conjecture of [Raman, Subedi, Raman, Tewari-24]. Quantitatively, we show that every class $\mathcal{H}$ is learnable with mistake bound $O \left(\sqrt{\mathtt{L}(\mathcal{H}) T \log T} \right)$ (where $\mathtt{L}(\mathcal{H})$ is the Littlestone dimension of $\mathcal{H}$), and that this is tight for some classes. We further study the agnostic case, in which the best hypothesis makes at most $k$ many mistakes, and prove a trichotomy stating that every class $\mathcal{H}$ must be either easy, hard, or unlearnable. Easy classes have (both randomized and deterministic) mistake bound $\Theta_{\mathcal{H}}(k)$. Hard classes have randomized mistake bound $\tilde{\Theta}_{\mathcal{H}} \left(k + \sqrt{T} \right)$, and deterministic mistake bound $\tilde{\Theta}_{\mathcal{H}} \left(\sqrt{k \cdot T} \right)$, where $T$ is the time horizon. Unlearnable classes have (both randomized and deterministic) mistake bound $\Theta(T)$. Our upper bound is based on a deterministic algorithm for learning from expert advice with apple tasting feedback, a problem interesting in its own right. For this problem, we show that the optimal deterministic mistake bound is $\Theta \left(\sqrt{T (k + \log n)} \right)$ for all $k$ and $T \leq n \leq 2^T$, where $n$ is the number of experts.

Dual VC Dimension Obstructs Sample Compression by Embeddings

This work studies embedding of arbitrary VC classes in well-behaved VC classes, focusing particularly on extremal classes. Our main result expresses an impossibility: such embeddings necessarily require a significant increase in dimension. In particular, we prove that for every $d$ there is a class with VC dimension $d$ that cannot be embedded in any extremal class of VC dimension smaller than exponential in $d$. In addition to its independent interest, this result has an important implication in learning theory, as it reveals a fundamental limitation of one of the most extensively studied approaches to tackling the long-standing sample compression conjecture. Concretely, the approach proposed by Floyd and Warmuth entails embedding any given VC class into an extremal class of a comparable dimension, and then applying an optimal sample compression scheme for extremal classes. However, our results imply that this strategy would in some cases result in a sample compression scheme at least exponentially larger than what is predicted by the sample compression conjecture. The above implications follow from a general result we prove: any extremal class with VC dimension $d$ has dual VC dimension at most $2d+1$. This bound is exponentially smaller than the classical bound $2^{d+1}-1$ of Assouad, which applies to general concept classes (and is known to be unimprovable for some classes). We in fact prove a stronger result, establishing that $2d+1$ upper bounds the dual Radon number of extremal classes. This theorem represents an abstraction of the classical Radon theorem for convex sets, extending its applicability to a wider combinatorial framework, without relying on the specifics of Euclidean convexity. The proof utilizes the topological method and is primarily based on variants of the Topological Radon Theorem.

Local Borsuk-Ulam, Stability, and Replicability

We use and adapt the Borsuk-Ulam Theorem from topology to derive limitations on list-replicable and globally stable learning algorithms. We further demonstrate the applicability of our methods in combinatorics and topology. We show that, besides trivial cases, both list-replicable and globally stable learning are impossible in the agnostic PAC setting. This is in contrast with the realizable case where it is known that any class with a finite Littlestone dimension can be learned by such algorithms. In the realizable PAC setting, we sharpen previous impossibility results and broaden their scope. Specifically, we establish optimal bounds for list replicability and global stability numbers in finite classes. This provides an exponential improvement over previous works and implies an exponential separation from the Littlestone dimension. We further introduce lower bounds for weak learners, i.e., learners that are only marginally better than random guessing. Lower bounds from previous works apply only to stronger learners. To offer a broader and more comprehensive view of our topological approach, we prove a local variant of the Borsuk-Ulam theorem in topology and a result in combinatorics concerning Kneser colorings. In combinatorics, we prove that if $c$ is a coloring of all non-empty subsets of $[n]$ such that disjoint sets have different colors, then there is a chain of subsets that receives at least $1+ \lfloor n/2\rfloor$ colors (this bound is sharp). In topology, we prove e.g. that for any open antipodal-free cover of the $d$-dimensional sphere, there is a point $x$ that belongs to at least $t=\lceil\frac{d+3}{2}\rceil$ sets.

Replicability and stability in learning

Replicability is essential in science as it allows us to validate and verify research findings. Impagliazzo, Lei, Pitassi and Sorrell (`22) recently initiated the study of replicability in machine learning. A learning algorithm is replicable if it typically produces the same output when applied on two i.i.d. inputs using the same internal randomness. We study a variant of replicability that does not involve fixing the randomness. An algorithm satisfies this form of replicability if it typically produces the same output when applied on two i.i.d. inputs (without fixing the internal randomness). This variant is called global stability and was introduced by Bun, Livni and Moran ('20) in the context of differential privacy. Impagliazzo et al. showed how to boost any replicable algorithm so that it produces the same output with probability arbitrarily close to 1. In contrast, we demonstrate that for numerous learning tasks, global stability can only be accomplished weakly, where the same output is produced only with probability bounded away from 1. To overcome this limitation, we introduce the concept of list replicability, which is equivalent to global stability. Moreover, we prove that list replicability can be boosted so that it is achieved with probability arbitrarily close to 1. We also describe basic relations between standard learning-theoretic complexity measures and list replicable numbers. Our results, in addition, imply that besides trivial cases, replicable algorithms (in the sense of Impagliazzo et al.) must be randomized. The proof of the impossibility result is based on a topological fixed-point theorem. For every algorithm, we are able to locate a "hard input distribution" by applying the Poincar\'{e}-Miranda theorem in a related topological setting. The equivalence between global stability and list replicability is algorithmic.

Optimally compressing VC classes

Resolving a conjecture of Littlestone and Warmuth, we show that any concept class of VC-dimension $d$ has a sample compression scheme of size $d$.

Collision Recovery Control of a Foldable Quadrotor

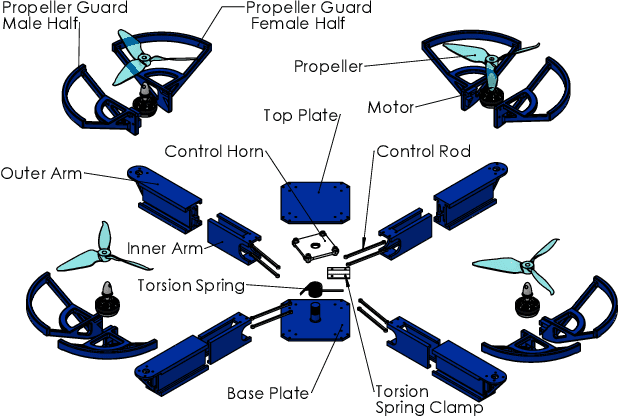
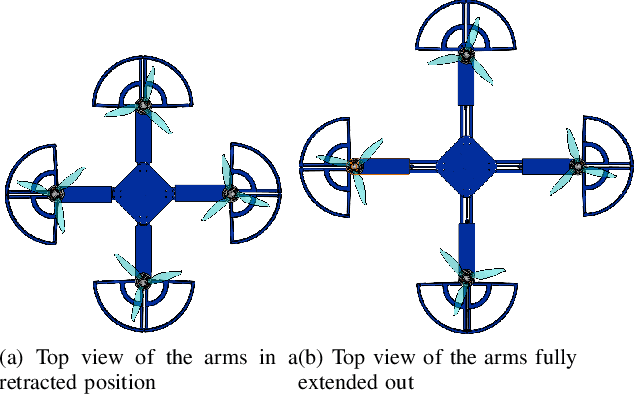
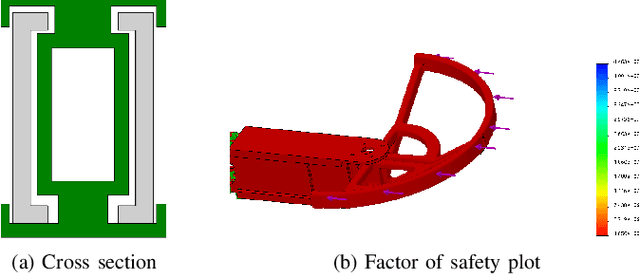
Autonomous missions of small unmanned aerial vehicles (UAVs) are prone to collisions owing to environmental disturbances and localization errors. Consequently, a UAV that can endure collisions and perform recovery control in critical aerial missions is desirable to prevent loss of the vehicle and/or payload. We address this problem by proposing a novel foldable quadrotor system which can sustain collisions and recover safely. The quadrotor is designed with integrated mechanical compliance using a torsional spring such that the impact time is increased and the net impact force on the main body is decreased. The post-collision dynamics is analysed and a recovery controller is proposed which stabilizes the system to a hovering location without additional collisions. Flight test results on the proposed and a conventional quadrotor demonstrate that for the former, integrated spring-damper characteristics reduce the rebound velocity and lead to simple recovery control algorithms in the event of unintended collisions as compared to a rigid quadrotor of the same dimension.

Experimental Evidence for Asymptotic Non-Optimality of Comb Adversary Strategy

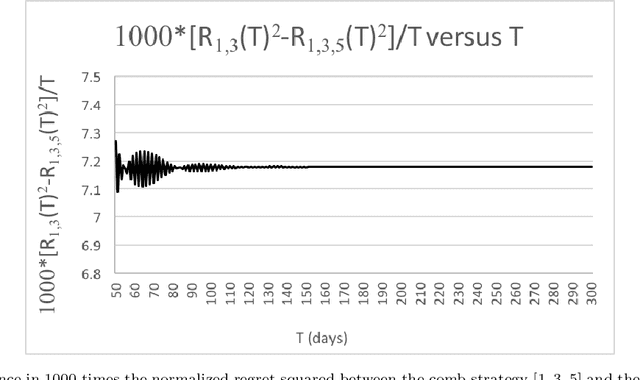
For the problem of prediction with expert advice in the adversarial setting with finite stopping time, we give strong computer evidence that the comb strategy for $k=5$ experts is not asymptotically optimal, thereby giving strong evidence against a conjecture of Gravin, Peres, and Sivan.

Learning Time Dependent Choice

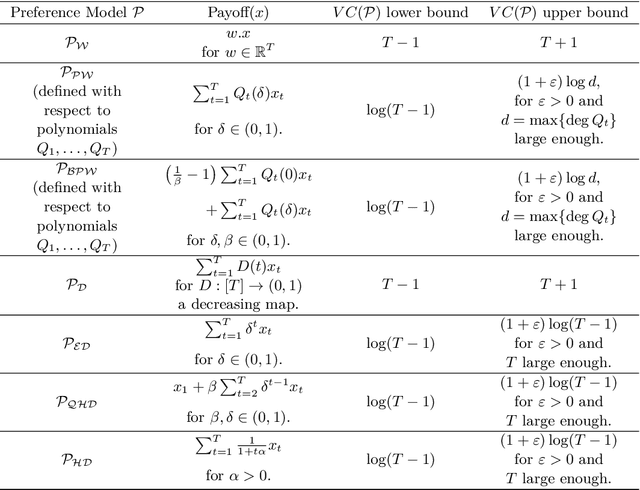
We explore questions dealing with the learnability of models of choice over time. We present a large class of preference models defined by a structural criterion for which we are able to obtain an exponential improvement over previously known learning bounds for more general preference models. This in particular implies that the three most important discounted utility models of intertemporal choice -- exponential, hyperbolic, and quasi-hyperbolic discounting -- are learnable in the PAC setting with VC dimension that grows logarithmically in the number of time periods. We also examine these models in the framework of active learning. We find that the commonly studied stream-based setting is in general difficult to analyze for preference models, but we provide a redeeming situation in which the learner can indeed improve upon the guarantees provided by PAC learning. In contrast to the stream-based setting, we show that if the learner is given full power over the data he learns from -- in the form of learning via membership queries -- even very naive algorithms significantly outperform the guarantees provided by higher level active learning algorithms.