Yuyi Wang
Symbolic Music Genre Transfer with CycleGAN
Sep 20, 2018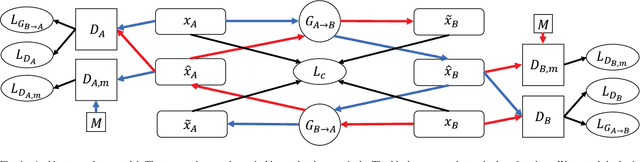
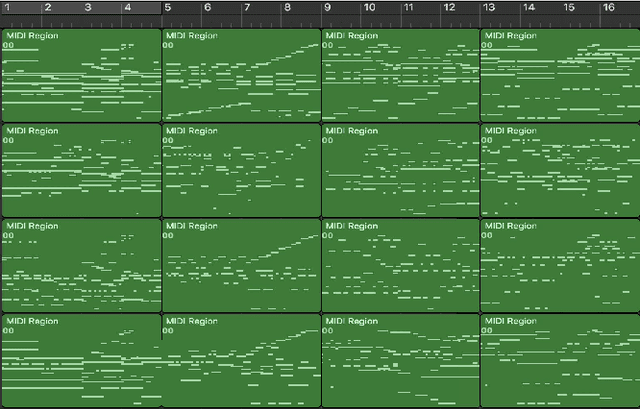

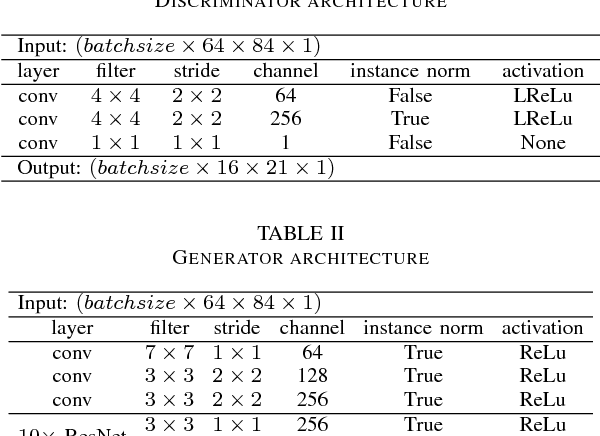
Abstract:Deep generative models such as Variational Autoencoders (VAEs) and Generative Adversarial Networks (GANs) have recently been applied to style and domain transfer for images, and in the case of VAEs, music. GAN-based models employing several generators and some form of cycle consistency loss have been among the most successful for image domain transfer. In this paper we apply such a model to symbolic music and show the feasibility of our approach for music genre transfer. Evaluations using separate genre classifiers show that the style transfer works well. In order to improve the fidelity of the transformed music, we add additional discriminators that cause the generators to keep the structure of the original music mostly intact, while still achieving strong genre transfer. Visual and audible results further show the potential of our approach. To the best of our knowledge, this paper represents the first application of GANs to symbolic music domain transfer.
PAC-Reasoning in Relational Domains
Jul 04, 2018Abstract:We consider the problem of predicting plausible missing facts in relational data, given a set of imperfect logical rules. In particular, our aim is to provide bounds on the (expected) number of incorrect inferences that are made in this way. Since for classical inference it is in general impossible to bound this number in a non-trivial way, we consider two inference relations that weaken, but remain close in spirit to classical inference.
VC-Dimension Based Generalization Bounds for Relational Learning
Jul 04, 2018Abstract:In many applications of relational learning, the available data can be seen as a sample from a larger relational structure (e.g. we may be given a small fragment from some social network). In this paper we are particularly concerned with scenarios in which we can assume that (i) the domain elements appearing in the given sample have been uniformly sampled without replacement from the (unknown) full domain and (ii) the sample is complete for these domain elements (i.e. it is the full substructure induced by these elements). Within this setting, we study bounds on the error of sufficient statistics of relational models that are estimated on the available data. As our main result, we prove a bound based on a variant of the Vapnik-Chervonenkis dimension which is suitable for relational data.
Relational Marginal Problems: Theory and Estimation
Apr 25, 2018Abstract:In the propositional setting, the marginal problem is to find a (maximum-entropy) distribution that has some given marginals. We study this problem in a relational setting and make the following contributions. First, we compare two different notions of relational marginals. Second, we show a duality between the resulting relational marginal problems and the maximum likelihood estimation of the parameters of relational models, which generalizes a well-known duality from the propositional setting. Third, by exploiting the relational marginal formulation, we present a statistically sound method to learn the parameters of relational models that will be applied in settings where the number of constants differs between the training and test data. Furthermore, based on a relational generalization of marginal polytopes, we characterize cases where the standard estimators based on feature's number of true groundings needs to be adjusted and we quantitatively characterize the consequences of these adjustments. Fourth, we prove bounds on expected errors of the estimated parameters, which allows us to lower-bound, among other things, the effective sample size of relational training data.
Natural Language Multitasking: Analyzing and Improving Syntactic Saliency of Hidden Representations
Jan 18, 2018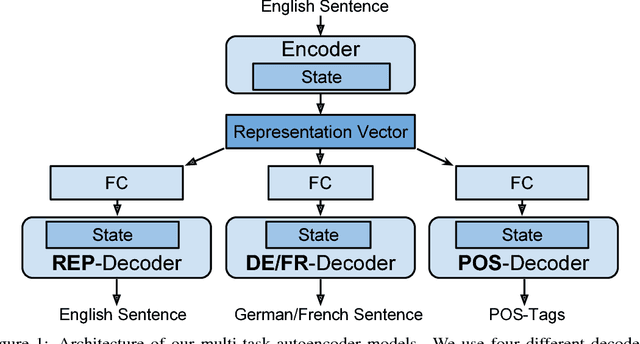
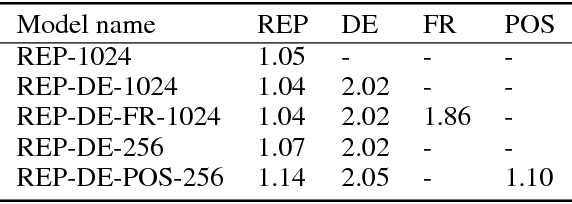


Abstract:We train multi-task autoencoders on linguistic tasks and analyze the learned hidden sentence representations. The representations change significantly when translation and part-of-speech decoders are added. The more decoders a model employs, the better it clusters sentences according to their syntactic similarity, as the representation space becomes less entangled. We explore the structure of the representation space by interpolating between sentences, which yields interesting pseudo-English sentences, many of which have recognizable syntactic structure. Lastly, we point out an interesting property of our models: The difference-vector between two sentences can be added to change a third sentence with similar features in a meaningful way.
On the ERM Principle with Networked Data
Nov 22, 2017
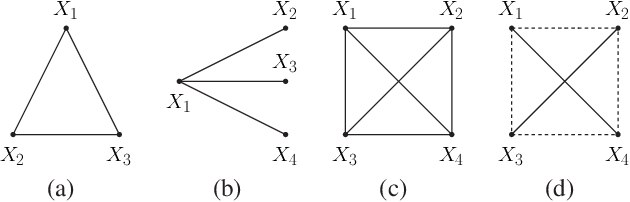
Abstract:Networked data, in which every training example involves two objects and may share some common objects with others, is used in many machine learning tasks such as learning to rank and link prediction. A challenge of learning from networked examples is that target values are not known for some pairs of objects. In this case, neither the classical i.i.d.\ assumption nor techniques based on complete U-statistics can be used. Most existing theoretical results of this problem only deal with the classical empirical risk minimization (ERM) principle that always weights every example equally, but this strategy leads to unsatisfactory bounds. We consider general weighted ERM and show new universal risk bounds for this problem. These new bounds naturally define an optimization problem which leads to appropriate weights for networked examples. Though this optimization problem is not convex in general, we devise a new fully polynomial-time approximation scheme (FPTAS) to solve it.
JamBot: Music Theory Aware Chord Based Generation of Polyphonic Music with LSTMs
Nov 21, 2017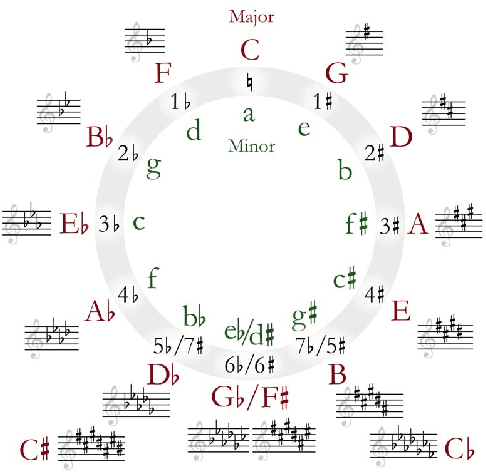
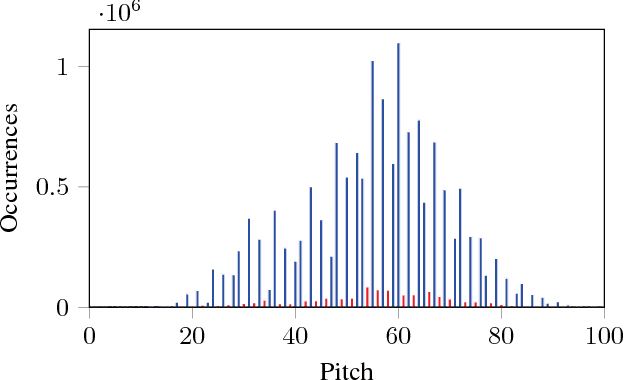
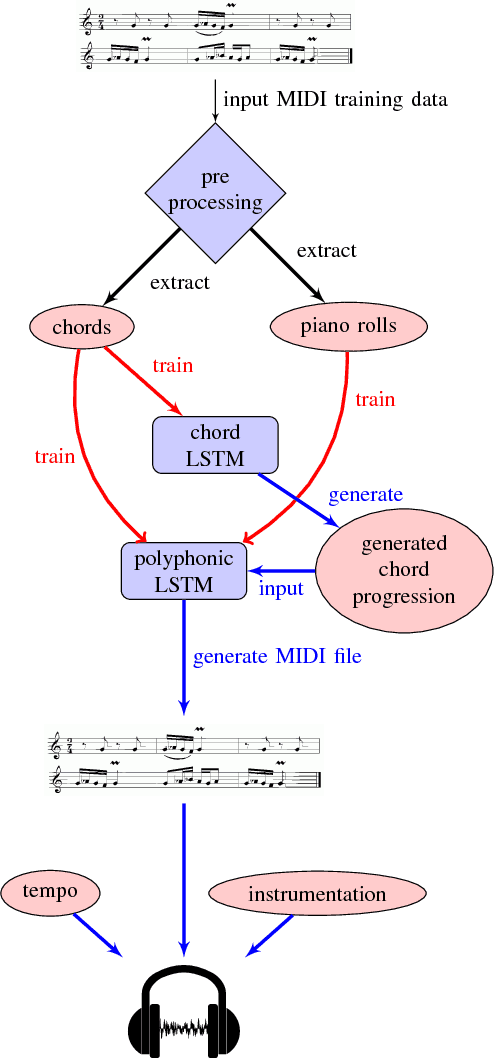
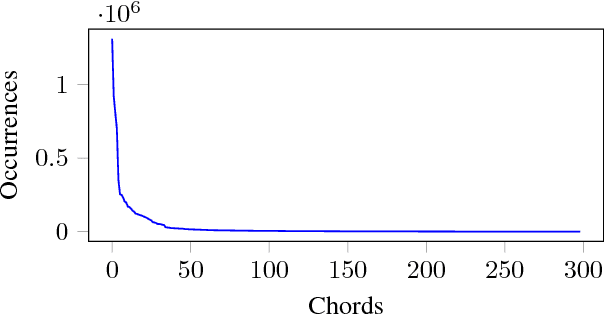
Abstract:We propose a novel approach for the generation of polyphonic music based on LSTMs. We generate music in two steps. First, a chord LSTM predicts a chord progression based on a chord embedding. A second LSTM then generates polyphonic music from the predicted chord progression. The generated music sounds pleasing and harmonic, with only few dissonant notes. It has clear long-term structure that is similar to what a musician would play during a jam session. We show that our approach is sensible from a music theory perspective by evaluating the learned chord embeddings. Surprisingly, our simple model managed to extract the circle of fifths, an important tool in music theory, from the dataset.
Teaching a Machine to Read Maps with Deep Reinforcement Learning
Nov 20, 2017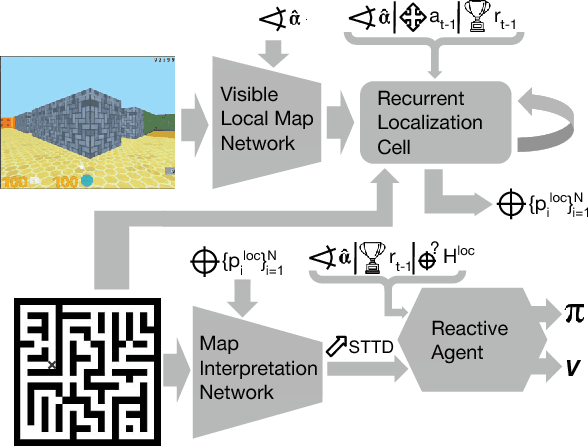
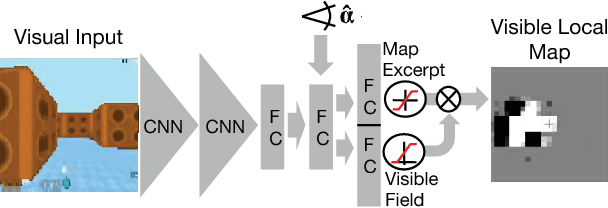
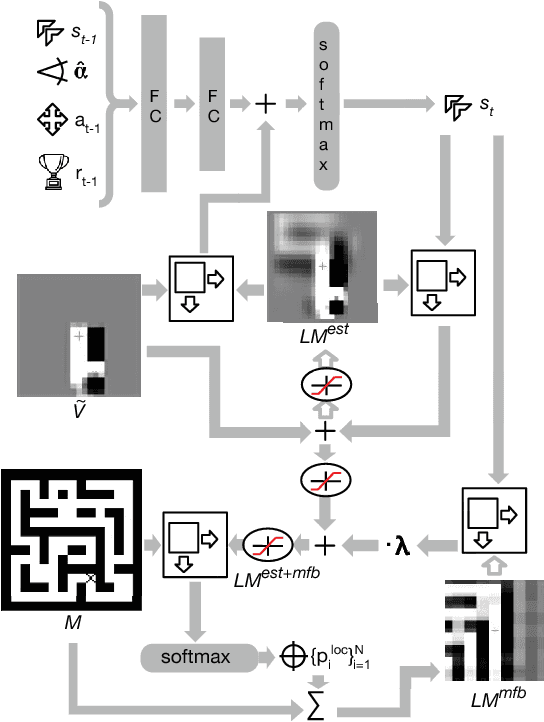
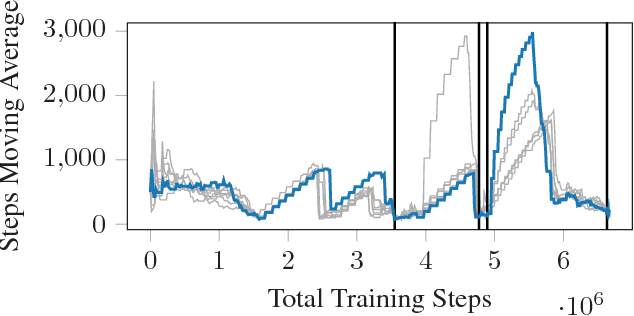
Abstract:The ability to use a 2D map to navigate a complex 3D environment is quite remarkable, and even difficult for many humans. Localization and navigation is also an important problem in domains such as robotics, and has recently become a focus of the deep reinforcement learning community. In this paper we teach a reinforcement learning agent to read a map in order to find the shortest way out of a random maze it has never seen before. Our system combines several state-of-the-art methods such as A3C and incorporates novel elements such as a recurrent localization cell. Our agent learns to localize itself based on 3D first person images and an approximate orientation angle. The agent generalizes well to bigger mazes, showing that it learned useful localization and navigation capabilities.
Learning from networked examples
Jun 03, 2017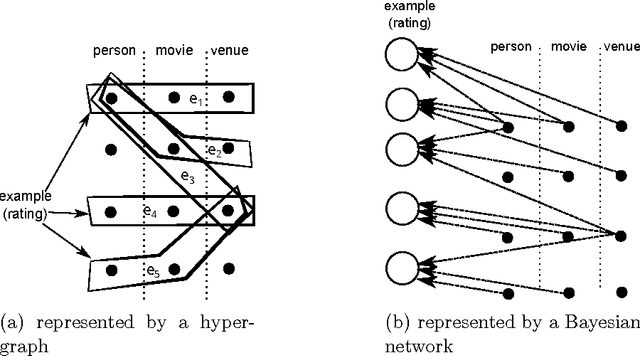
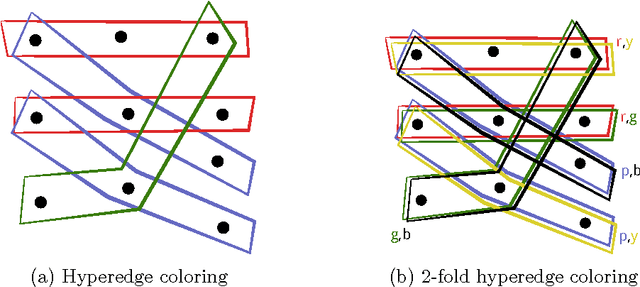
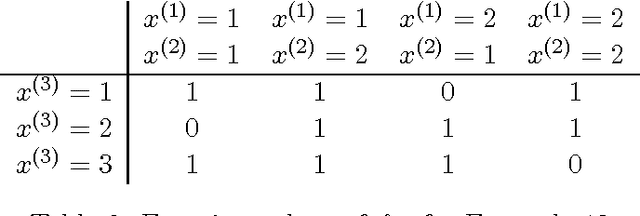
Abstract:Many machine learning algorithms are based on the assumption that training examples are drawn independently. However, this assumption does not hold anymore when learning from a networked sample because two or more training examples may share some common objects, and hence share the features of these shared objects. We show that the classic approach of ignoring this problem potentially can have a harmful effect on the accuracy of statistics, and then consider alternatives. One of these is to only use independent examples, discarding other information. However, this is clearly suboptimal. We analyze sample error bounds in this networked setting, providing significantly improved results. An important component of our approach is formed by efficient sample weighting schemes, which leads to novel concentration inequalities.
Learning from networked examples in a k-partite graph
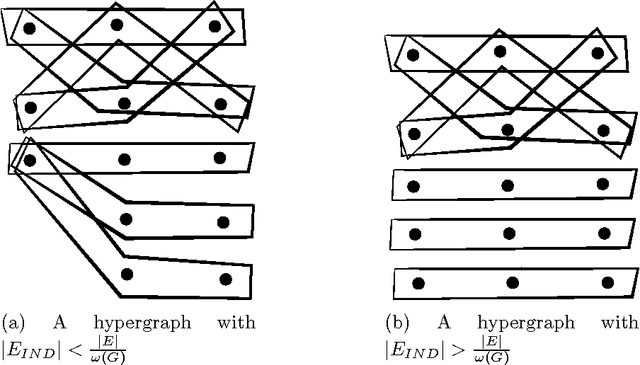
Feb 18, 2017
Abstract:Many machine learning algorithms are based on the assumption that training examples are drawn independently. However, this assumption does not hold anymore when learning from a networked sample where two or more training examples may share common features. We propose an efficient weighting method for learning from networked examples and show the sample error bound which is better than previous work.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge