Yuanhong Wang
Tractable Weighted First-Order Model Counting with Bounded Treewidth Binary Evidence
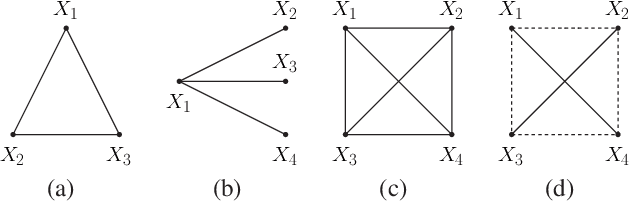
Nov 12, 2025Abstract:The Weighted First-Order Model Counting Problem (WFOMC) asks to compute the weighted sum of models of a given first-order logic sentence over a given domain. Conditioning WFOMC on evidence -- fixing the truth values of a set of ground literals -- has been shown impossible in time polynomial in the domain size (unless $\mathsf{\#P \subseteq FP}$) even for fragments of logic that are otherwise tractable for WFOMC without evidence. In this work, we address the barrier by restricting the binary evidence to the case where the underlying Gaifman graph has bounded treewidth. We present a polynomial-time algorithm in the domain size for computing WFOMC for the two-variable fragments $\text{FO}^2$ and $\text{C}^2$ conditioned on such binary evidence. Furthermore, we show the applicability of our algorithm in combinatorial problems by solving the stable seating arrangement problem on bounded-treewidth graphs of bounded degree, which was an open problem. We also conducted experiments to show the scalability of our algorithm compared to the existing model counting solvers.
Model Enumeration of Two-Variable Logic with Quadratic Delay Complexity
May 26, 2025Abstract:We study the model enumeration problem of the function-free, finite domain fragment of first-order logic with two variables ($FO^2$). Specifically, given an $FO^2$ sentence $\Gamma$ and a positive integer $n$, how can one enumerate all the models of $\Gamma$ over a domain of size $n$? In this paper, we devise a novel algorithm to address this problem. The delay complexity, the time required between producing two consecutive models, of our algorithm is quadratic in the given domain size $n$ (up to logarithmic factors) when the sentence is fixed. This complexity is almost optimal since the interpretation of binary predicates in any model requires at least $\Omega(n^2)$ bits to represent.
Bridging Weighted First Order Model Counting and Graph Polynomials
Jul 16, 2024



Abstract:The Weighted First-Order Model Counting Problem (WFOMC) asks to compute the weighted sum of models of a given first-order logic sentence over a given domain. It can be solved in time polynomial in the domain size for sentences from the two-variable fragment with counting quantifiers, known as $C^2$. This polynomial-time complexity is also retained when extending $C^2$ by one of the following axioms: linear order axiom, tree axiom, forest axiom, directed acyclic graph axiom or connectedness axiom. An interesting question remains as to which other axioms can be added to the first-order sentences in this way. We provide a new perspective on this problem by associating WFOMC with graph polynomials. Using WFOMC, we define Weak Connectedness Polynomial and Strong Connectedness Polynomials for first-order logic sentences. It turns out that these polynomials have the following interesting properties. First, they can be computed in polynomial time in the domain size for sentences from $C^2$. Second, we can use them to solve WFOMC with all of the existing axioms known to be tractable as well as with new ones such as bipartiteness, strong connectedness, being a spanning subgraph, having $k$ connected components, etc. Third, the well-known Tutte polynomial can be recovered as a special case of the Weak Connectedness Polynomial, and the Strict and Non-Strict Directed Chromatic Polynomials can be recovered from the Strong Connectedness Polynomials, which allows us to show that these important graph polynomials can be computed in time polynomial in the number of vertices for any graph that can be encoded by a fixed $C^2$ sentence and a conjunction of an arbitrary number of ground unary literals.
Lifted Algorithms for Symmetric Weighted First-Order Model Sampling
Aug 21, 2023



Abstract:Weighted model counting (WMC) is the task of computing the weighted sum of all satisfying assignments (i.e., models) of a propositional formula. Similarly, weighted model sampling (WMS) aims to randomly generate models with probability proportional to their respective weights. Both WMC and WMS are hard to solve exactly, falling under the $\#\mathsf{P}$-hard complexity class. However, it is known that the counting problem may sometimes be tractable, if the propositional formula can be compactly represented and expressed in first-order logic. In such cases, model counting problems can be solved in time polynomial in the domain size, and are known as domain-liftable. The following question then arises: Is it also the case for weighted model sampling? This paper addresses this question and answers it affirmatively. Specifically, we prove the domain-liftability under sampling for the two-variables fragment of first-order logic with counting quantifiers in this paper, by devising an efficient sampling algorithm for this fragment that runs in time polynomial in the domain size. We then further show that this result continues to hold even in the presence of cardinality constraints. To empirically verify our approach, we conduct experiments over various first-order formulas designed for the uniform generation of combinatorial structures and sampling in statistical-relational models. The results demonstrate that our algorithm outperforms a start-of-the-art WMS sampler by a substantial margin, confirming the theoretical results.
On Exact Sampling in the Two-Variable Fragment of First-Order Logic
Feb 06, 2023



Abstract:In this paper, we study the sampling problem for first-order logic proposed recently by Wang et al. -- how to efficiently sample a model of a given first-order sentence on a finite domain? We extend their result for the universally-quantified subfragment of two-variable logic $\mathbf{FO}^2$ ($\mathbf{UFO}^2$) to the entire fragment of $\mathbf{FO}^2$. Specifically, we prove the domain-liftability under sampling of $\mathbf{FO}^2$, meaning that there exists a sampling algorithm for $\mathbf{FO}^2$ that runs in time polynomial in the domain size. We then further show that this result continues to hold even in the presence of counting constraints, such as $\forall x\exists_{=k} y: \varphi(x,y)$ and $\exists_{=k} x\forall y: \varphi(x,y)$, for some quantifier-free formula $\varphi(x,y)$. Our proposed method is constructive, and the resulting sampling algorithms have potential applications in various areas, including the uniform generation of combinatorial structures and sampling in statistical-relational models such as Markov logic networks and probabilistic logic programs.
On the ERM Principle with Networked Data
Nov 22, 2017
Abstract:Networked data, in which every training example involves two objects and may share some common objects with others, is used in many machine learning tasks such as learning to rank and link prediction. A challenge of learning from networked examples is that target values are not known for some pairs of objects. In this case, neither the classical i.i.d.\ assumption nor techniques based on complete U-statistics can be used. Most existing theoretical results of this problem only deal with the classical empirical risk minimization (ERM) principle that always weights every example equally, but this strategy leads to unsatisfactory bounds. We consider general weighted ERM and show new universal risk bounds for this problem. These new bounds naturally define an optimization problem which leads to appropriate weights for networked examples. Though this optimization problem is not convex in general, we devise a new fully polynomial-time approximation scheme (FPTAS) to solve it.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge