DualKanbaFormer: Kolmogorov-Arnold Networks and State Space Model Transformer for Multimodal Aspect-based Sentiment Analysis

Multimodal aspect-based sentiment analysis (MABSA) enhances sentiment detection by combining text with other data types like images. However, despite setting significant benchmarks, attention mechanisms exhibit limitations in efficiently modelling long-range dependencies between aspect and opinion targets within the text. They also face challenges in capturing global-context dependencies for visual representations. To this end, we propose Kolmogorov-Arnold Networks (KANs) and Selective State Space model (Mamba) transformer (DualKanbaFormer), a novel architecture to address the above issues. We leverage the power of Mamba to capture global context dependencies, Multi-head Attention (MHA) to capture local context dependencies, and KANs to capture non-linear modelling patterns for both textual representations (textual KanbaFormer) and visual representations (visual KanbaFormer). Furthermore, we fuse the textual KanbaFormer and visual KanbaFomer with a gated fusion layer to capture the inter-modality dynamics. According to extensive experimental results, our model outperforms some state-of-the-art (SOTA) studies on two public datasets.

MambaForGCN: Enhancing Long-Range Dependency with State Space Model and Kolmogorov-Arnold Networks for Aspect-Based Sentiment Analysis

Aspect-based sentiment Analysis (ABSA) identifies and evaluates sentiments toward specific aspects of entities within text, providing detailed insights beyond overall sentiment. However, Attention mechanisms and neural network models struggle with syntactic constraints, and the quadratic complexity of attention mechanisms hinders their adoption for capturing long-range dependencies between aspect and opinion words in ABSA. This complexity can lead to the misinterpretation of irrelevant con-textual words, restricting their effectiveness to short-range dependencies. Some studies have investigated merging semantic and syntactic approaches but face challenges in effectively integrating these methods. To address the above problems, we present MambaForGCN, a novel approach to enhance short and long-range dependencies between aspect and opinion words in ABSA. This innovative approach incorporates syntax-based Graph Convolutional Network (SynGCN) and MambaFormer (Mamba-Transformer) modules to encode input with dependency relations and semantic information. The Multihead Attention (MHA) and Mamba blocks in the MambaFormer module serve as channels to enhance the model with short and long-range dependencies between aspect and opinion words. We also introduce the Kolmogorov-Arnold Networks (KANs) gated fusion, an adaptively integrated feature representation system combining SynGCN and MambaFormer representations. Experimental results on three benchmark datasets demonstrate MambaForGCN's effectiveness, outperforming state-of-the-art (SOTA) baseline models.

Lifted Algorithms for Symmetric Weighted First-Order Model Sampling

Weighted model counting (WMC) is the task of computing the weighted sum of all satisfying assignments (i.e., models) of a propositional formula. Similarly, weighted model sampling (WMS) aims to randomly generate models with probability proportional to their respective weights. Both WMC and WMS are hard to solve exactly, falling under the $\#\mathsf{P}$-hard complexity class. However, it is known that the counting problem may sometimes be tractable, if the propositional formula can be compactly represented and expressed in first-order logic. In such cases, model counting problems can be solved in time polynomial in the domain size, and are known as domain-liftable. The following question then arises: Is it also the case for weighted model sampling? This paper addresses this question and answers it affirmatively. Specifically, we prove the domain-liftability under sampling for the two-variables fragment of first-order logic with counting quantifiers in this paper, by devising an efficient sampling algorithm for this fragment that runs in time polynomial in the domain size. We then further show that this result continues to hold even in the presence of cardinality constraints. To empirically verify our approach, we conduct experiments over various first-order formulas designed for the uniform generation of combinatorial structures and sampling in statistical-relational models. The results demonstrate that our algorithm outperforms a start-of-the-art WMS sampler by a substantial margin, confirming the theoretical results.

On Exact Sampling in the Two-Variable Fragment of First-Order Logic

In this paper, we study the sampling problem for first-order logic proposed recently by Wang et al. -- how to efficiently sample a model of a given first-order sentence on a finite domain? We extend their result for the universally-quantified subfragment of two-variable logic $\mathbf{FO}^2$ ($\mathbf{UFO}^2$) to the entire fragment of $\mathbf{FO}^2$. Specifically, we prove the domain-liftability under sampling of $\mathbf{FO}^2$, meaning that there exists a sampling algorithm for $\mathbf{FO}^2$ that runs in time polynomial in the domain size. We then further show that this result continues to hold even in the presence of counting constraints, such as $\forall x\exists_{=k} y: \varphi(x,y)$ and $\exists_{=k} x\forall y: \varphi(x,y)$, for some quantifier-free formula $\varphi(x,y)$. Our proposed method is constructive, and the resulting sampling algorithms have potential applications in various areas, including the uniform generation of combinatorial structures and sampling in statistical-relational models such as Markov logic networks and probabilistic logic programs.

On the ERM Principle with Networked Data

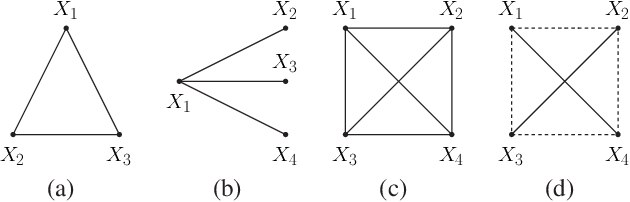
Networked data, in which every training example involves two objects and may share some common objects with others, is used in many machine learning tasks such as learning to rank and link prediction. A challenge of learning from networked examples is that target values are not known for some pairs of objects. In this case, neither the classical i.i.d.\ assumption nor techniques based on complete U-statistics can be used. Most existing theoretical results of this problem only deal with the classical empirical risk minimization (ERM) principle that always weights every example equally, but this strategy leads to unsatisfactory bounds. We consider general weighted ERM and show new universal risk bounds for this problem. These new bounds naturally define an optimization problem which leads to appropriate weights for networked examples. Though this optimization problem is not convex in general, we devise a new fully polynomial-time approximation scheme (FPTAS) to solve it.