Geometric ergodicity of SGLD via reflection coupling

We consider the geometric ergodicity of the Stochastic Gradient Langevin Dynamics (SGLD) algorithm under nonconvexity settings. Via the technique of reflection coupling, we prove the Wasserstein contraction of SGLD when the target distribution is log-concave only outside some compact set. The time discretization and the minibatch in SGLD introduce several difficulties when applying the reflection coupling, which are addressed by a series of careful estimates of conditional expectations. As a direct corollary, the SGLD with constant step size has an invariant distribution and we are able to obtain its geometric ergodicity in terms of $W_1$ distance. The generalization to non-gradient drifts is also included.

A sharp uniform-in-time error estimate for Stochastic Gradient Langevin Dynamics

We establish a sharp uniform-in-time error estimate for the Stochastic Gradient Langevin Dynamics (SGLD), which is a popular sampling algorithm. Under mild assumptions, we obtain a uniform-in-time $O(\eta^2)$ bound for the KL-divergence between the SGLD iteration and the Langevin diffusion, where $\eta$ is the step size (or learning rate). Our analysis is also valid for varying step sizes. Based on this, we are able to obtain an $O(\eta)$ bound for the distance between the SGLD iteration and the invariant distribution of the Langevin diffusion, in terms of Wasserstein or total variation distances.

On uniform-in-time diffusion approximation for stochastic gradient descent

The diffusion approximation of stochastic gradient descent (SGD) in current literature is only valid on a finite time interval. In this paper, we establish the uniform-in-time diffusion approximation of SGD, by only assuming that the expected loss is strongly convex and some other mild conditions, without assuming the convexity of each random loss function. The main technique is to establish the exponential decay rates of the derivatives of the solution to the backward Kolmogorov equation. The uniform-in-time approximation allows us to study asymptotic behaviors of SGD via the continuous stochastic differential equation (SDE) even when the random objective function $f(\cdot;\xi)$ is not strongly convex.

Topic-aware chatbot using Recurrent Neural Networks and Nonnegative Matrix Factorization

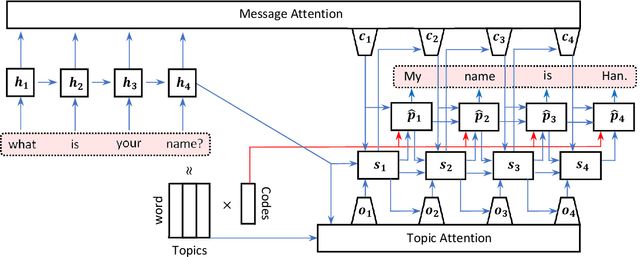
We propose a novel model for a topic-aware chatbot by combining the traditional Recurrent Neural Network (RNN) encoder-decoder model with a topic attention layer based on Nonnegative Matrix Factorization (NMF). After learning topic vectors from an auxiliary text corpus via NMF, the decoder is trained so that it is more likely to sample response words from the most correlated topic vectors. One of the main advantages in our architecture is that the user can easily switch the NMF-learned topic vectors so that the chatbot obtains desired topic-awareness. We demonstrate our model by training on a single conversational data set which is then augmented with topic matrices learned from different auxiliary data sets. We show that our topic-aware chatbot not only outperforms the non-topic counterpart, but also that each topic-aware model qualitatively and contextually gives the most relevant answer depending on the topic of question.