Robust Pivoting: Exploiting Frictional Stability Using Bilevel Optimization

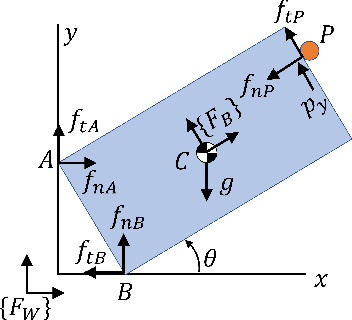
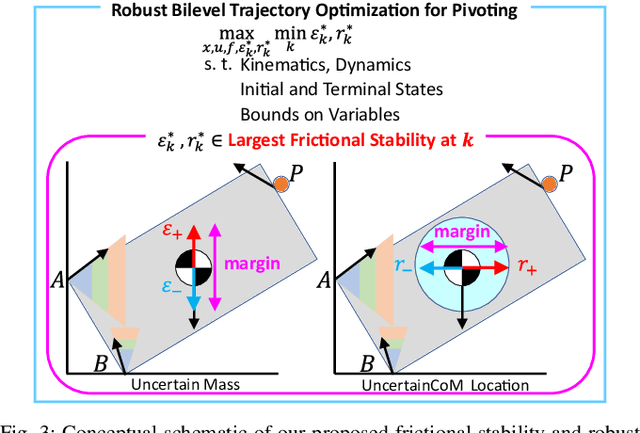
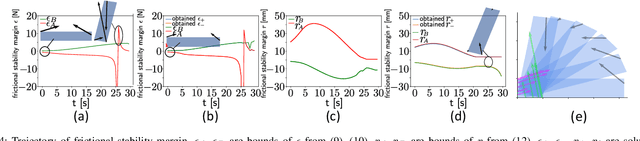
Generalizable manipulation requires that robots be able to interact with novel objects and environment. This requirement makes manipulation extremely challenging as a robot has to reason about complex frictional interaction with uncertainty in physical properties of the object. In this paper, we study robust optimization for control of pivoting manipulation in the presence of uncertainties. We present insights about how friction can be exploited to compensate for the inaccuracies in the estimates of the physical properties during manipulation. In particular, we derive analytical expressions for stability margin provided by friction during pivoting manipulation. This margin is then used in a bilevel trajectory optimization algorithm to design a controller that maximizes this stability margin to provide robustness against uncertainty in physical properties of the object. We demonstrate our proposed method using a 6 DoF manipulator for manipulating several different objects.

Chance-Constrained Optimization in Contact-Rich Systems for Robust Manipulation

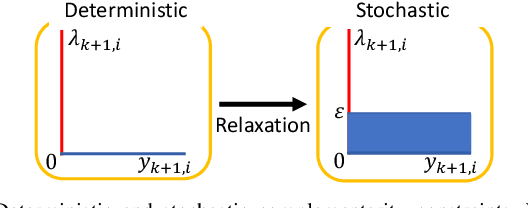
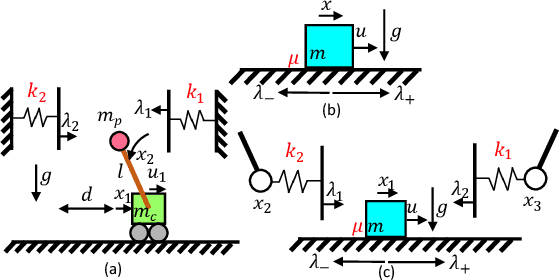
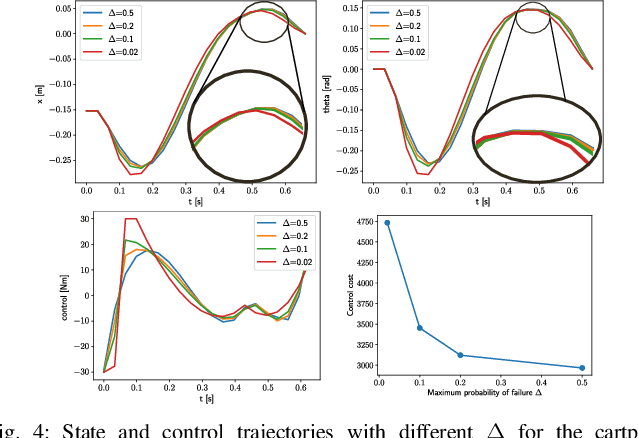
This paper presents a chance-constrained formulation for robust trajectory optimization during manipulation. In particular, we present a chance-constrained optimization for Stochastic Discrete-time Linear Complementarity Systems (SDLCS). To solve the optimization problem, we formulate Mixed-Integer Quadratic Programming with Chance Constraints (MIQPCC). In our formulation, we explicitly consider joint chance constraints for complementarity as well as states to capture the stochastic evolution of dynamics. We evaluate robustness of our optimized trajectories in simulation on several systems. The proposed approach outperforms some recent approaches for robust trajectory optimization for SDLCS.

An Under-Actuated Whippletree Mechanism Gripper based on Multi-Objective Design Optimization with Auto-Tuned Weights

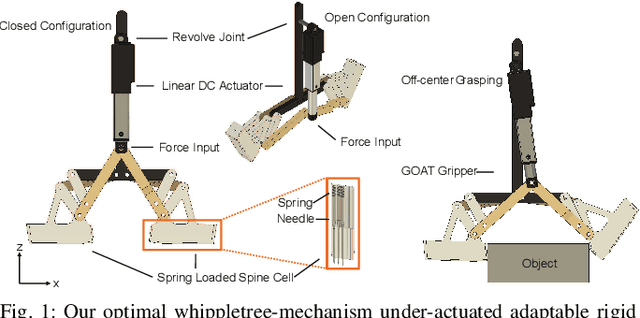
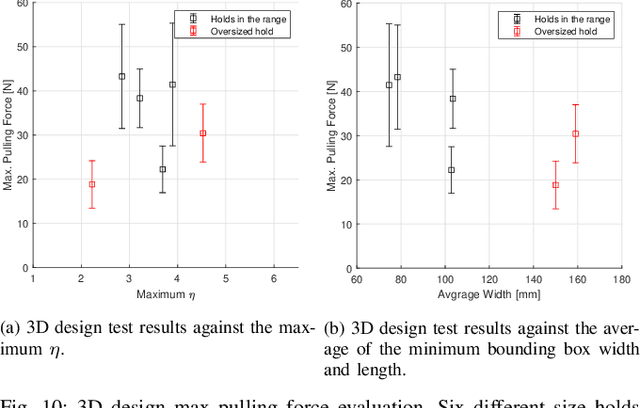
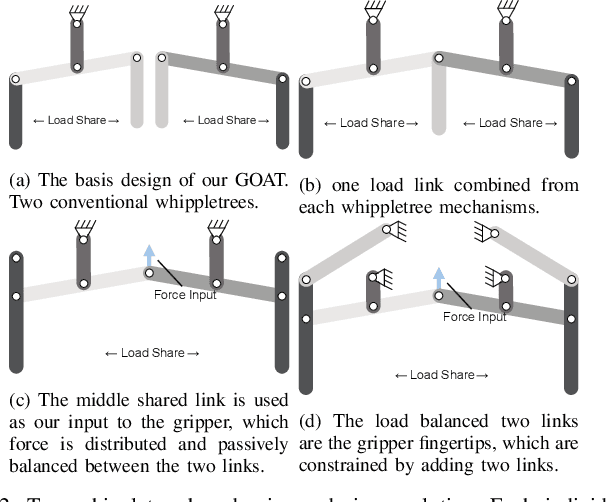
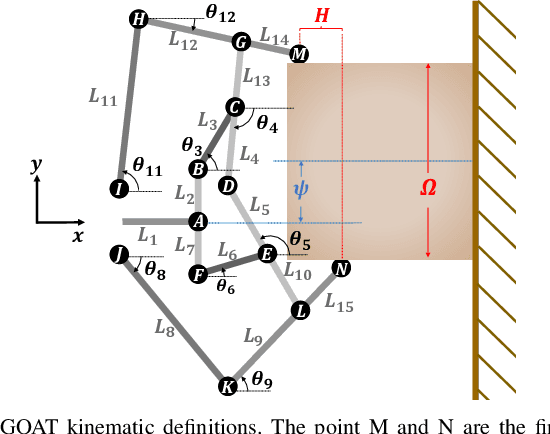
Current rigid linkage grippers are limited in flexibility, and gripper design optimality relies on expertise, experiments, or arbitrary parameters. Our proposed rigid gripper can accommodate irregular and off-center objects through a whippletree mechanism, improving adaptability. We present a whippletree-based rigid under-actuated gripper and its parametric design multi-objective optimization for a one-wall climbing task. Our proposed objective function considers kinematics and grasping forces simultaneously with a mathematical metric based on a model of an object environment. Our multi-objective problem is formulated as a single kinematic objective function with auto-tuning force-based weight. Our results indicate that our proposed objective function determines optimal parameters and kinematic ranges for our under-actuated gripper in the task environment with sufficient grasping forces.

LTO: Lazy Trajectory Optimization with Graph-Search Planning for High DOF Robots in Cluttered Environments

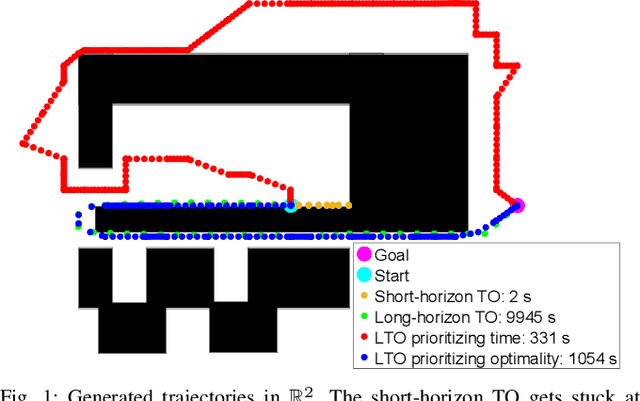
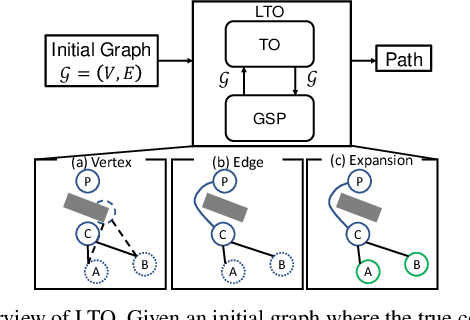
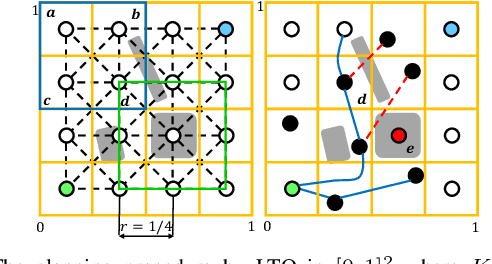
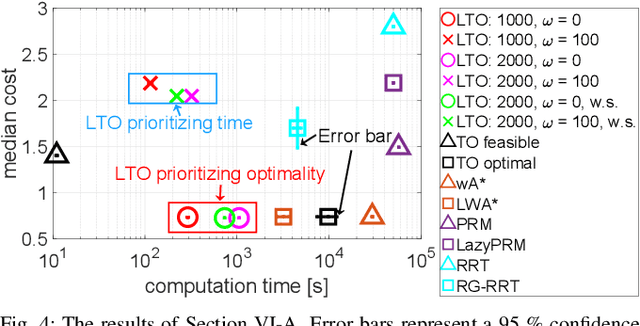
Although Trajectory Optimization (TO) is one of the most powerful motion planning tools, it suffers from expensive computational complexity as a time horizon increases in cluttered environments. It can also fail to converge to a globally optimal solution. In this paper, we present Lazy Trajectory Optimization (LTO) that unifies local short-horizon TO and global Graph-Search Planning (GSP) to generate a long-horizon global optimal trajectory. LTO solves TO with the same constraints as the original long-horizon TO with improved time complexity. We also propose a TO-aware cost function that can balance both solution cost and planning time. Since LTO solves many nearly identical TO in a roadmap, it can provide an informed warm-start for TO to accelerate the planning process. We also present proofs of the computational complexity and optimality of LTO. Finally, we demonstrate LTO's performance on motion planning problems for a 2 DOF free-flying robot and a 21 DOF legged robot, showing that LTO outperforms existing algorithms in terms of its runtime and reliability.

Risk-Aware Motion Planning for a Limbed Robot with Stochastic Gripping Forces Using Nonlinear Programming

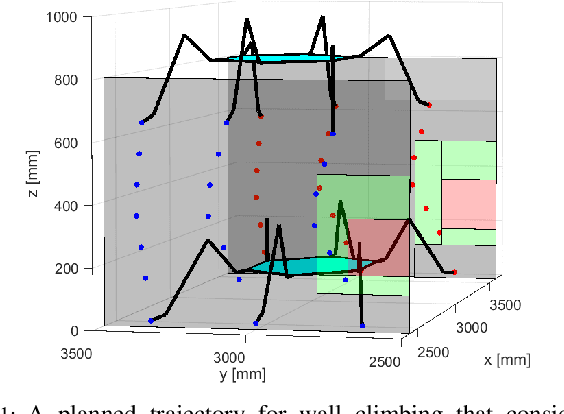
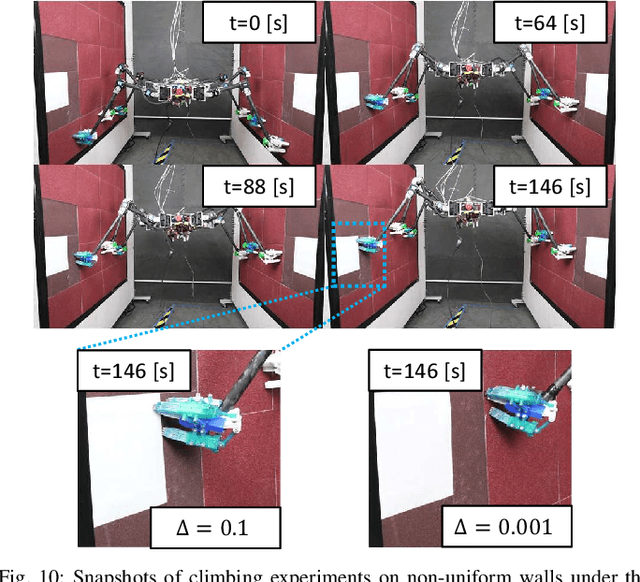
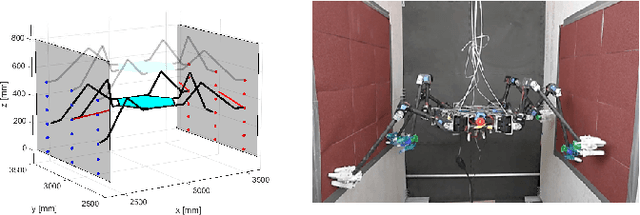
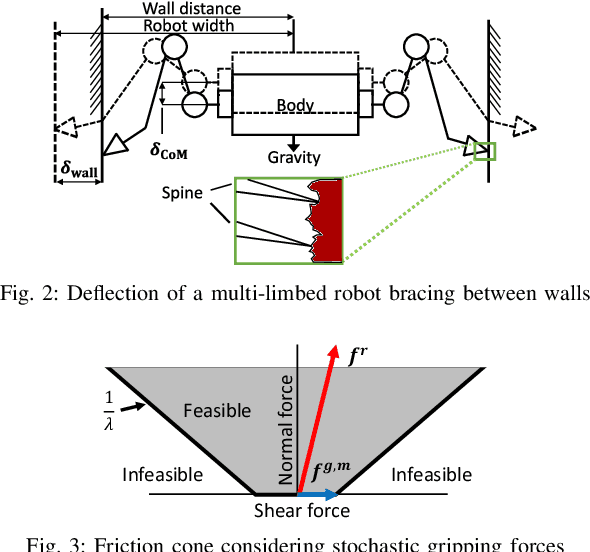
We present a motion planning algorithm with probabilistic guarantees for limbed robots with stochastic gripping forces. Planners based on deterministic models with a worst-case uncertainty can be conservative and inflexible to consider the stochastic behavior of the contact, especially when a gripper is installed. Our proposed planner enables the robot to simultaneously plan its pose and contact force trajectories while considering the risk associated with the gripping forces. Our planner is formulated as a nonlinear programming problem with chance constraints, which allows the robot to generate a variety of motions based on different risk bounds. To model the gripping forces as random variables, we employ Gaussian Process regression. We validate our proposed motion planning algorithm on an 11.5 kg six-limbed robot for two-wall climbing. Our results show that our proposed planner generates various trajectories (e.g., avoiding low friction terrain under the low risk bound, choosing an unstable but faster gait under the high risk bound) by changing the probability of risk based on various specifications.