Multi-Constrained Evolutionary Molecular Design Framework: An Interpretable Drug Design Method Combining Rule-Based Evolution and Molecular Crossover

This study proposes MCEMOL (Multi-Constrained Evolutionary Molecular Design Framework), a molecular optimization approach integrating rule-based evolution with molecular crossover. MCEMOL employs dual-layer evolution: optimizing transformation rules at rule level while applying crossover and mutation to molecular structures. Unlike deep learning methods requiring large datasets and extensive training, our algorithm evolves efficiently from minimal starting molecules with low computational overhead. The framework incorporates message-passing neural networks and comprehensive chemical constraints, ensuring efficient and interpretable molecular design. Experimental results demonstrate that MCEMOL provides transparent design pathways through its evolutionary mechanism while generating valid, diverse, target-compliant molecules. The framework achieves 100% molecular validity with high structural diversity and excellent drug-likeness compliance, showing strong performance in symmetry constraints, pharmacophore optimization, and stereochemical integrity. Unlike black-box methods, MCEMOL delivers dual value: interpretable transformation rules researchers can understand and trust, alongside high-quality molecular libraries for practical applications. This establishes a paradigm where interpretable AI-driven drug design and effective molecular generation are achieved simultaneously, bridging the gap between computational innovation and practical drug discovery needs.

Theoretical foundation for CMA-ES from information geometric perspective

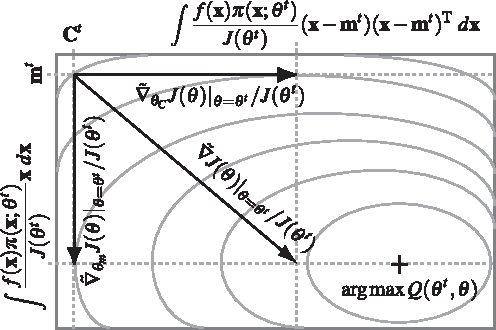
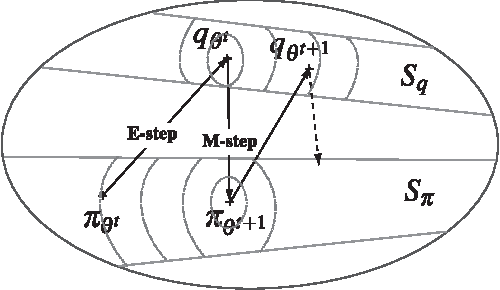
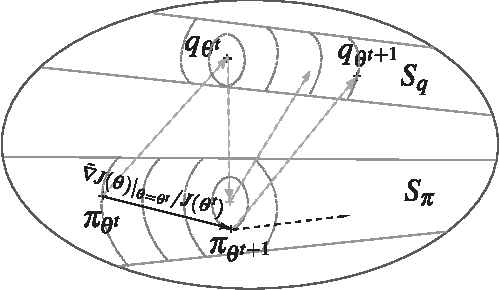
This paper explores the theoretical basis of the covariance matrix adaptation evolution strategy (CMA-ES) from the information geometry viewpoint. To establish a theoretical foundation for the CMA-ES, we focus on a geometric structure of a Riemannian manifold of probability distributions equipped with the Fisher metric. We define a function on the manifold which is the expectation of fitness over the sampling distribution, and regard the goal of update of the parameters of sampling distribution in the CMA-ES as maximization of the expected fitness. We investigate the steepest ascent learning for the expected fitness maximization, where the steepest ascent direction is given by the natural gradient, which is the product of the inverse of the Fisher information matrix and the conventional gradient of the function. Our first result is that we can obtain under some types of parameterization of multivariate normal distribution the natural gradient of the expected fitness without the need for inversion of the Fisher information matrix. We find that the update of the distribution parameters in the CMA-ES is the same as natural gradient learning for expected fitness maximization. Our second result is that we derive the range of learning rates such that a step in the direction of the exact natural gradient improves the parameters in the expected fitness. We see from the close relation between the CMA-ES and natural gradient learning that the default setting of learning rates in the CMA-ES seems suitable in terms of monotone improvement in expected fitness. Then, we discuss the relation to the expectation-maximization framework and provide an information geometric interpretation of the CMA-ES.