RVI-SAC: Average Reward Off-Policy Deep Reinforcement Learning

In this paper, we propose an off-policy deep reinforcement learning (DRL) method utilizing the average reward criterion. While most existing DRL methods employ the discounted reward criterion, this can potentially lead to a discrepancy between the training objective and performance metrics in continuing tasks, making the average reward criterion a recommended alternative. We introduce RVI-SAC, an extension of the state-of-the-art off-policy DRL method, Soft Actor-Critic (SAC), to the average reward criterion. Our proposal consists of (1) Critic updates based on RVI Q-learning, (2) Actor updates introduced by the average reward soft policy improvement theorem, and (3) automatic adjustment of Reset Cost enabling the average reward reinforcement learning to be applied to tasks with termination. We apply our method to the Gymnasium's Mujoco tasks, a subset of locomotion tasks, and demonstrate that RVI-SAC shows competitive performance compared to existing methods.

CMA-ES with Learning Rate Adaptation

The covariance matrix adaptation evolution strategy (CMA-ES) is one of the most successful methods for solving continuous black-box optimization problems. A practically useful aspect of the CMA-ES is that it can be used without hyperparameter tuning. However, the hyperparameter settings still have a considerable impact on performance, especially for difficult tasks, such as solving multimodal or noisy problems. This study comprehensively explores the impact of learning rate on the CMA-ES performance and demonstrates the necessity of a small learning rate by considering ordinary differential equations. Thereafter, it discusses the setting of an ideal learning rate. Based on these discussions, we develop a novel learning rate adaptation mechanism for the CMA-ES that maintains a constant signal-to-noise ratio. Additionally, we investigate the behavior of the CMA-ES with the proposed learning rate adaptation mechanism through numerical experiments, and compare the results with those obtained for the CMA-ES with a fixed learning rate and with population size adaptation. The results show that the CMA-ES with the proposed learning rate adaptation works well for multimodal and/or noisy problems without extremely expensive learning rate tuning.

Natural Evolution Strategy for Mixed-Integer Black-Box Optimization

This paper proposes a natural evolution strategy (NES) for mixed-integer black-box optimization (MI-BBO) that appears in real-world problems such as hyperparameter optimization of machine learning and materials design. This problem is difficult to optimize because plateaus where the values do not change appear when the integer variables are relaxed to the continuous ones. CMA-ES w. Margin that addresses the plateaus reportedly showed good performance on MI-BBO benchmark problems. However, it has been observed that the search performance of CMA-ES w. Margin deteriorates when continuous variables contribute more to the objective function value than integer ones. In order to address the problem of CMA-ES w. Margin, we propose Distance-weighted eXponential Natural Evolution Strategy taking account of Implicit Constraint and Integer (DX-NES-ICI). We compare the search performance of DX-NES-ICI with that of CMA-ES w. Margin through numerical experiments. As a result, DX-NES-ICI was up to 3.7 times better than CMA-ES w. Margin in terms of a rate of finding the optimal solutions on benchmark problems where continuous variables contribute more to the objective function value than integer ones. DX-NES-ICI also outperformed CMA-ES w. Margin on problems where CMA-ES w. Margin originally showed good performance.

CMA-ES with Learning Rate Adaptation: Can CMA-ES with Default Population Size Solve Multimodal and Noisy Problems?

The covariance matrix adaptation evolution strategy (CMA-ES) is one of the most successful methods for solving black-box continuous optimization problems. One practically useful aspect of the CMA-ES is that it can be used without hyperparameter tuning. However, the hyperparameter settings still have a considerable impact, especially for difficult tasks such as solving multimodal or noisy problems. In this study, we investigate whether the CMA-ES with default population size can solve multimodal and noisy problems. To perform this investigation, we develop a novel learning rate adaptation mechanism for the CMA-ES, such that the learning rate is adapted so as to maintain a constant signal-to-noise ratio. We investigate the behavior of the CMA-ES with the proposed learning rate adaptation mechanism through numerical experiments, and compare the results with those obtained for the CMA-ES with a fixed learning rate. The results demonstrate that, when the proposed learning rate adaptation is used, the CMA-ES with default population size works well on multimodal and/or noisy problems, without the need for extremely expensive learning rate tuning.

Fast Moving Natural Evolution Strategy for High-Dimensional Problems

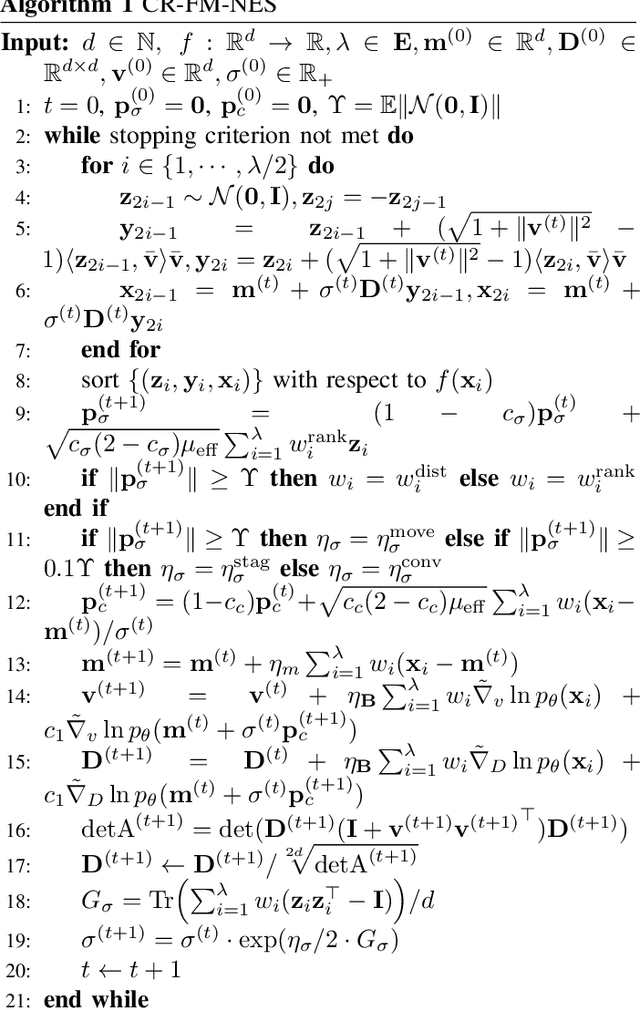
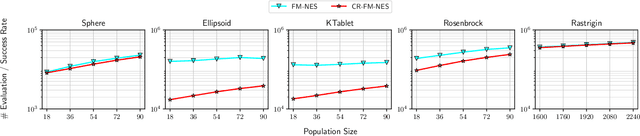
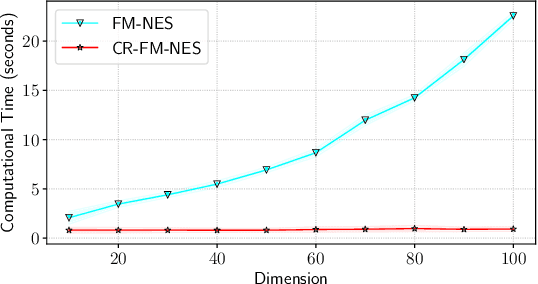
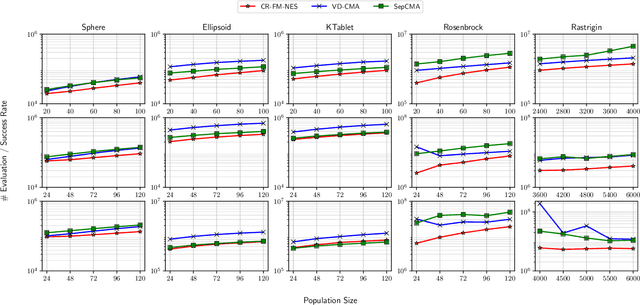
In this work, we propose a new variant of natural evolution strategies (NES) for high-dimensional black-box optimization problems. The proposed method, CR-FM-NES, extends a recently proposed state-of-the-art NES, Fast Moving Natural Evolution Strategy (FM-NES), in order to be applicable in high-dimensional problems. CR-FM-NES builds on an idea using a restricted representation of a covariance matrix instead of using a full covariance matrix, while inheriting an efficiency of FM-NES. The restricted representation of the covariance matrix enables CR-FM-NES to update parameters of a multivariate normal distribution in linear time and space complexity, which can be applied to high-dimensional problems. Our experimental results reveal that CR-FM-NES does not lose the efficiency of FM-NES, and on the contrary, CR-FM-NES has achieved significant speedup compared to FM-NES on some benchmark problems. Furthermore, our numerical experiments using 200, 600, and 1000-dimensional benchmark problems demonstrate that CR-FM-NES is effective over scalable baseline methods, VD-CMA and Sep-CMA.

Natural Evolution Strategy for Unconstrained and Implicitly Constrained Problems with Ridge Structure

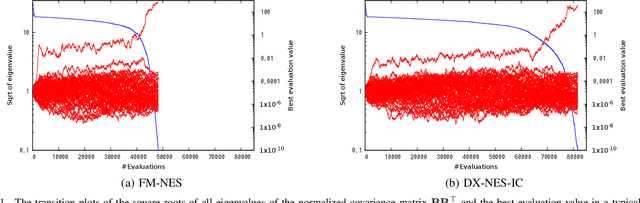
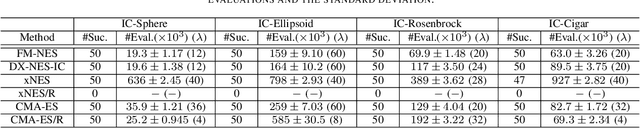
In this paper, we propose a new natural evolution strategy for unconstrained black-box function optimization (BBFO) problems and implicitly constrained BBFO problems. BBFO problems are known to be difficult because explicit representations of objective functions are not available. Implicit constraints make the problems more difficult because whether or not a solution is feasible is revealed when the solution is evaluated with the objective function. DX-NES-IC is one of the promising methods for implicitly constrained BBFO problems. DX-NES-IC has shown better performance than conventional methods on implicitly constrained benchmark problems. However, DX-NES-IC has a problem in that the moving speed of the probability distribution is slow on ridge structure. To address the problem, we propose the Fast Moving Natural Evolution Strategy (FM-NES) that accelerates the movement of the probability distribution on ridge structure by introducing the rank-one update into DX-NES-IC. The rank-one update is utilized in CMA-ES. Since naively introducing the rank-one update makes the search performance deteriorate on implicitly constrained problems, we propose a condition of performing the rank-one update. We also propose to reset the shape of the probability distribution when an infeasible solution is sampled at the first time. In numerical experiments using unconstrained and implicitly constrained benchmark problems, FM-NES showed better performance than DX-NES-IC on problems with ridge structure and almost the same performance as DX-NES-IC on the others. Furthermore, FM-NES outperformed xNES, CMA-ES, xNES with the resampling technique, and CMA-ES with the resampling technique.

Theoretical foundation for CMA-ES from information geometric perspective

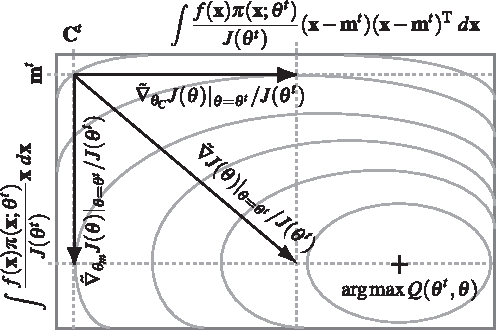
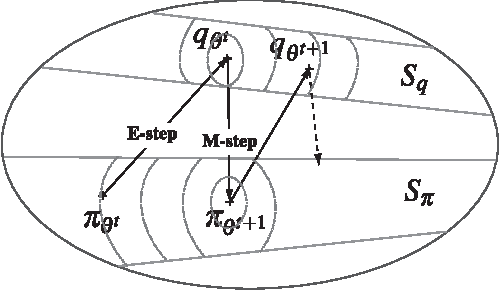
This paper explores the theoretical basis of the covariance matrix adaptation evolution strategy (CMA-ES) from the information geometry viewpoint. To establish a theoretical foundation for the CMA-ES, we focus on a geometric structure of a Riemannian manifold of probability distributions equipped with the Fisher metric. We define a function on the manifold which is the expectation of fitness over the sampling distribution, and regard the goal of update of the parameters of sampling distribution in the CMA-ES as maximization of the expected fitness. We investigate the steepest ascent learning for the expected fitness maximization, where the steepest ascent direction is given by the natural gradient, which is the product of the inverse of the Fisher information matrix and the conventional gradient of the function. Our first result is that we can obtain under some types of parameterization of multivariate normal distribution the natural gradient of the expected fitness without the need for inversion of the Fisher information matrix. We find that the update of the distribution parameters in the CMA-ES is the same as natural gradient learning for expected fitness maximization. Our second result is that we derive the range of learning rates such that a step in the direction of the exact natural gradient improves the parameters in the expected fitness. We see from the close relation between the CMA-ES and natural gradient learning that the default setting of learning rates in the CMA-ES seems suitable in terms of monotone improvement in expected fitness. Then, we discuss the relation to the expectation-maximization framework and provide an information geometric interpretation of the CMA-ES.