SuperLoc: The Key to Robust LiDAR-Inertial Localization Lies in Predicting Alignment Risks

Map-based LiDAR localization, while widely used in autonomous systems, faces significant challenges in degraded environments due to lacking distinct geometric features. This paper introduces SuperLoc, a robust LiDAR localization package that addresses key limitations in existing methods. SuperLoc features a novel predictive alignment risk assessment technique, enabling early detection and mitigation of potential failures before optimization. This approach significantly improves performance in challenging scenarios such as corridors, tunnels, and caves. Unlike existing degeneracy mitigation algorithms that rely on post-optimization analysis and heuristic thresholds, SuperLoc evaluates the localizability of raw sensor measurements. Experimental results demonstrate significant performance improvements over state-of-the-art methods across various degraded environments. Our approach achieves a 54% increase in accuracy and exhibits the highest robustness. To facilitate further research, we release our implementation along with datasets from eight challenging scenarios

Disentangled sticky hierarchical Dirichlet process hidden Markov model

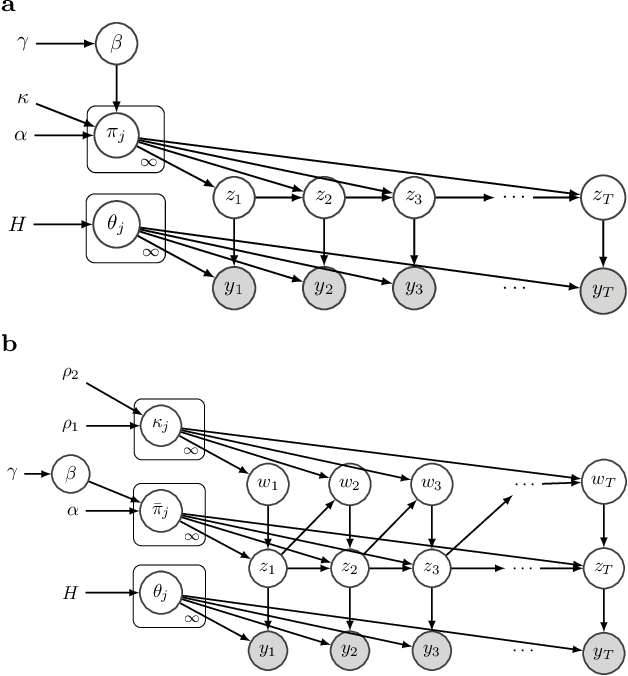
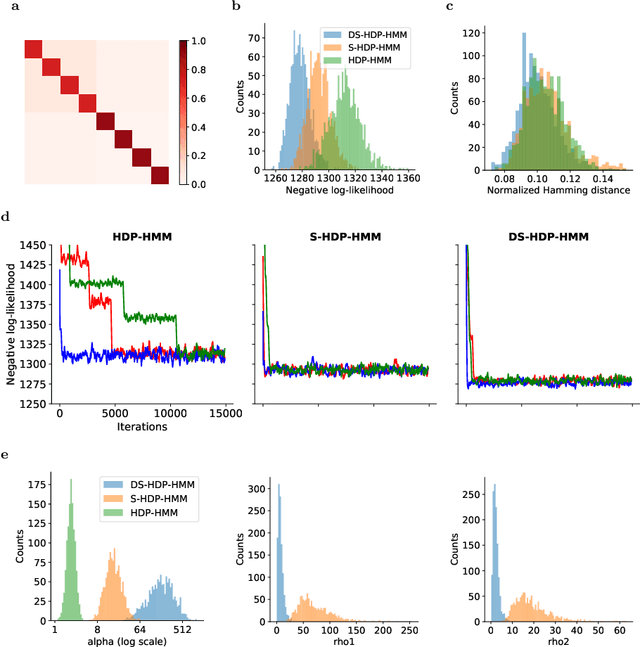
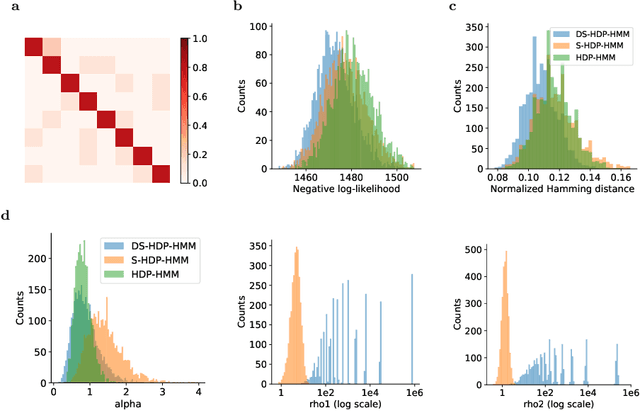
The Hierarchical Dirichlet Process Hidden Markov Model (HDP-HMM) has been used widely as a natural Bayesian nonparametric extension of the classical Hidden Markov Model for learning from sequential and time-series data. A sticky extension of the HDP-HMM has been proposed to strengthen the self-persistence probability in the HDP-HMM. However, the sticky HDP-HMM entangles the strength of the self-persistence prior and transition prior together, limiting its expressiveness. Here, we propose a more general model: the disentangled sticky HDP-HMM (DS-HDP-HMM). We develop novel Gibbs sampling algorithms for efficient inference in this model. We show that the disentangled sticky HDP-HMM outperforms the sticky HDP-HMM and HDP-HMM on both synthetic and real data, and apply the new approach to analyze neural data and segment behavioral video data.

Maximum Entropy Flow Networks

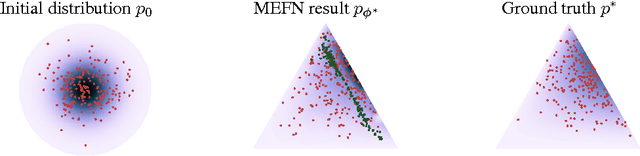
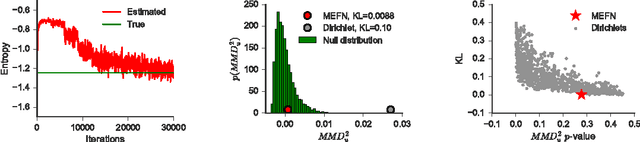
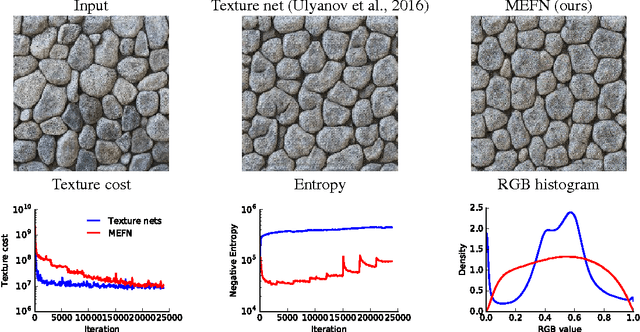
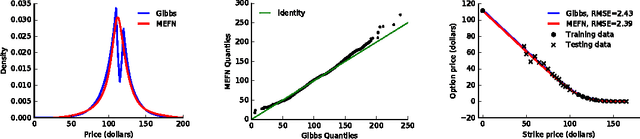
Maximum entropy modeling is a flexible and popular framework for formulating statistical models given partial knowledge. In this paper, rather than the traditional method of optimizing over the continuous density directly, we learn a smooth and invertible transformation that maps a simple distribution to the desired maximum entropy distribution. Doing so is nontrivial in that the objective being maximized (entropy) is a function of the density itself. By exploiting recent developments in normalizing flow networks, we cast the maximum entropy problem into a finite-dimensional constrained optimization, and solve the problem by combining stochastic optimization with the augmented Lagrangian method. Simulation results demonstrate the effectiveness of our method, and applications to finance and computer vision show the flexibility and accuracy of using maximum entropy flow networks.

Linear dynamical neural population models through nonlinear embeddings

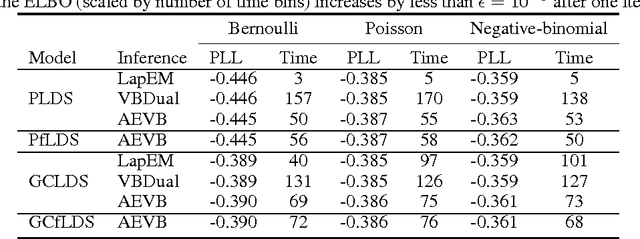
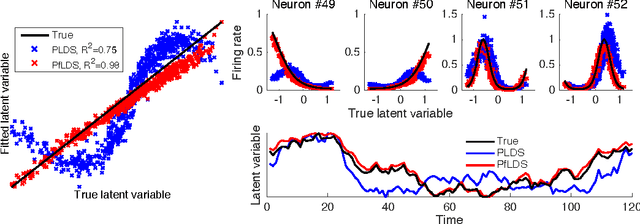
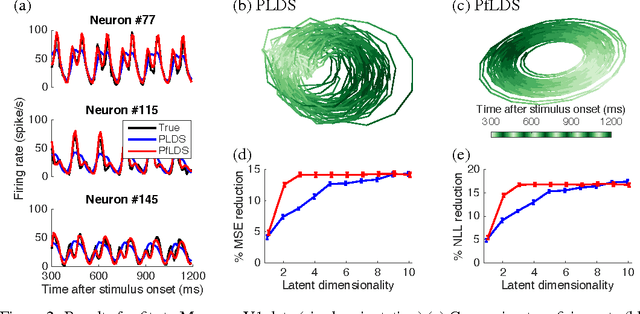
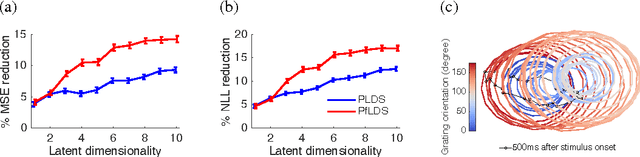
A body of recent work in modeling neural activity focuses on recovering low-dimensional latent features that capture the statistical structure of large-scale neural populations. Most such approaches have focused on linear generative models, where inference is computationally tractable. Here, we propose fLDS, a general class of nonlinear generative models that permits the firing rate of each neuron to vary as an arbitrary smooth function of a latent, linear dynamical state. This extra flexibility allows the model to capture a richer set of neural variability than a purely linear model, but retains an easily visualizable low-dimensional latent space. To fit this class of non-conjugate models we propose a variational inference scheme, along with a novel approximate posterior capable of capturing rich temporal correlations across time. We show that our techniques permit inference in a wide class of generative models.We also show in application to two neural datasets that, compared to state-of-the-art neural population models, fLDS captures a much larger proportion of neural variability with a small number of latent dimensions, providing superior predictive performance and interpretability.