Harnessing the Power of Large Language Models for Natural Language to First-Order Logic Translation

Translating natural language sentences to first-order logic (NL-FOL translation) is a longstanding challenge in the NLP and formal logic literature. This paper introduces LogicLLaMA, a LLaMA-7B model fine-tuned for NL-FOL translation using LoRA on a single GPU. LogicLLaMA is capable of directly translating natural language into FOL rules, which outperforms GPT-3.5. LogicLLaMA is also equipped to correct FOL rules predicted by GPT-3.5, and can achieve similar performance as GPT-4 with a fraction of the cost. This correction ability was achieved by a novel supervised fine-tuning (SFT) + reinforcement learning with human feedback (RLHF) framework, which initially trains on synthetically perturbed NL-FOL pairs to encourage chain-of-thought reasoning and then fine-tunes with RLHF on GPT-3.5 outputs using a FOL verifier as the reward model. To train LogicLLaMA, we present MALLS (large language $\textbf{M}$odel gener$\textbf{A}$ted N$\textbf{L}$-FO$\textbf{L}$ pair$\textbf{S}$), a dataset of 34K high-quality and diverse sentence-level NL-FOL pairs collected from GPT-4. The dataset was created by implementing a pipeline that prompts GPT-4 for pairs, and dynamically adjusts the prompts to ensure the collection of pairs with rich and diverse contexts at different levels of complexity, and verifies the validity of the generated FOL rules. Codes, weights, and data are available at $\href{https://github.com/gblackout/LogicLLaMA}{{\small \text{https://github.com/gblackout/LogicLLaMA}}}$.

An Approach for Solving Tasks on the Abstract Reasoning Corpus

The Abstract Reasoning Corpus (ARC) is an intelligence tests for measuring fluid intelligence in artificial intelligence systems and humans alike. In this paper we present a system for reasoning about and solving ARC tasks. Our system relies on a program synthesis approach that searches a space of potential programs for ones that can solve tasks from the ARC. Programs are in a domain specific language, and in some instances our search algorithm is guided by insights from a corpus of ground truth programs. In particular: We describe an imperative style domain specific language, called Visual Imagery Reasoning Language (VIMRL), for reasoning about tasks in the ARC. We also demonstrate an innovative approach for how large search spaces can be decomposed using special high level functions that determine their own arguments through local searches on a given task item. Finally, we share our results obtained on the publicly available ARC items as well as our system's strong performance on a private test, recently tying for 4th place on the global ARCathon 2022 challenge.

Deep Non-Monotonic Reasoning for Visual Abstract Reasoning Tasks

While achieving unmatched performance on many well-defined tasks, deep learning models have also been used to solve visual abstract reasoning tasks, which are relatively less well-defined, and have been widely used to measure human intelligence. However, current deep models struggle to match human abilities to solve such tasks with minimum data but maximum generalization. One limitation is that current deep learning models work in a monotonic way, i.e., treating different parts of the input in essentially fixed orderings, whereas people repeatedly observe and reason about the different parts of the visual stimuli until the reasoning process converges to a consistent conclusion, i.e., non-monotonic reasoning. This paper proposes a non-monotonic computational approach to solve visual abstract reasoning tasks. In particular, we implemented a deep learning model using this approach and tested it on the RAVEN dataset -- a dataset inspired by the Raven's Progressive Matrices test. Results show that the proposed approach is more effective than existing monotonic deep learning models, under strict experimental settings that represent a difficult variant of the RAVEN dataset problem.

Computational Models of Solving Raven's Progressive Matrices: A Comprehensive Introduction

As being widely used to measure human intelligence, Raven's Progressive Matrices (RPM) tests also pose a great challenge for AI systems. There is a long line of computational models for solving RPM, starting from 1960s, either to understand the involved cognitive processes or solely for problem-solving purposes. Due to the dramatic paradigm shifts in AI researches, especially the advent of deep learning models in the last decade, the computational studies on RPM have also changed a lot. Therefore, now is a good time to look back at this long line of research. As the title -- ``a comprehensive introduction'' -- indicates, this paper provides an all-in-one presentation of computational models for solving RPM, including the history of RPM, intelligence testing theories behind RPM, item design and automatic item generation of RPM-like tasks, a conceptual chronicle of computational models for solving RPM, which reveals the philosophy behind the technology evolution of these models, and suggestions for transferring human intelligence testing and AI testing.

Visual-Imagery-Based Analogical Construction in Geometric Matrix Reasoning Task

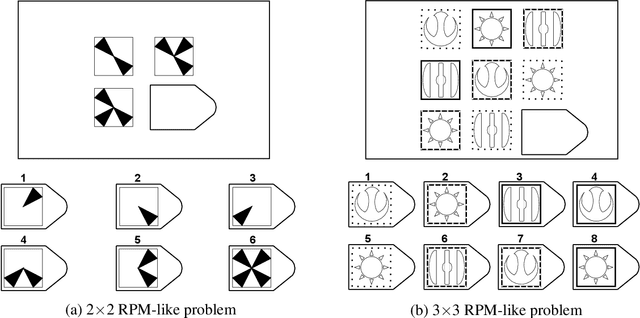
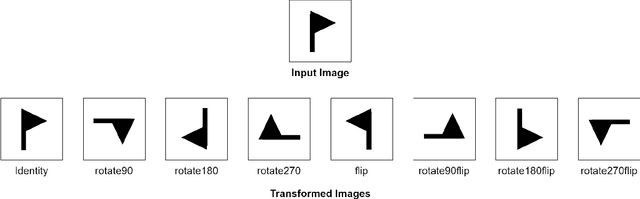
Raven's Progressive Matrices is a family of classical intelligence tests that have been widely used in both research and clinical settings. There have been many exciting efforts in AI communities to computationally model various aspects of problem solving such figural analogical reasoning problems. In this paper, we present a series of computational models for solving Raven's Progressive Matrices using analogies and image transformations. We run our models following three different strategies usually adopted by human testees. These models are tested on the standard version of Raven's Progressive Matrices, in which we can solve 57 out 60 problems in it. Therefore, analogy and image transformation are proved to be effective in solving RPM problems.

Temporal Inductive Logic Reasoning

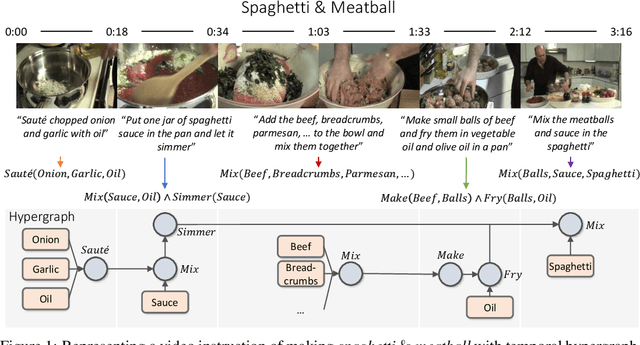
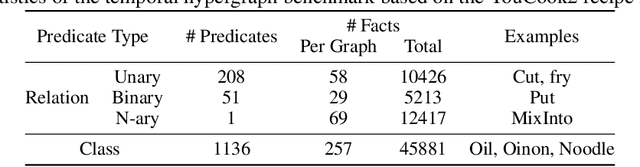
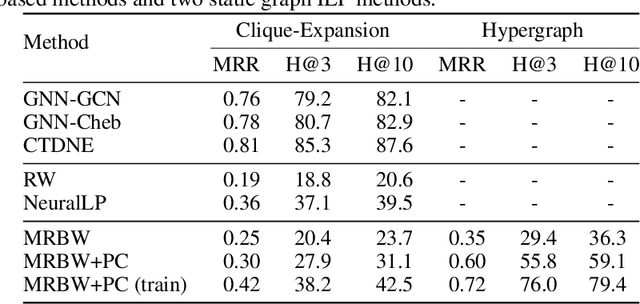
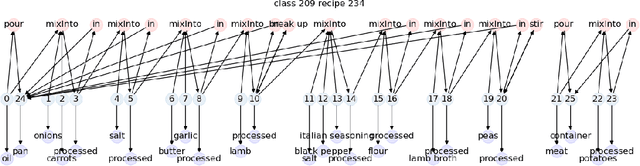
Inductive logic reasoning is one of the fundamental tasks on graphs, which seeks to generalize patterns from the data. This task has been studied extensively for traditional graph datasets such as knowledge graphs (KGs), with representative techniques such as inductive logic programming (ILP). Existing ILP methods typically assume learning from KGs with static facts and binary relations. Beyond KGs, graph structures are widely present in other applications such as video instructions, scene graphs and program executions. While inductive logic reasoning is also beneficial for these applications, applying ILP to the corresponding graphs is nontrivial: they are more complex than KGs, which usually involve timestamps and n-ary relations, effectively a type of hypergraph with temporal events. In this work, we study two of such applications and propose to represent them as hypergraphs with time intervals. To reason on this graph, we propose the multi-start random B-walk that traverses this hypergraph. Combining it with a path-consistency algorithm, we propose an efficient backward-chaining ILP method that learns logic rules by generalizing from both the temporal and the relational data.

Neural MoCon: Neural Motion Control for Physically Plausible Human Motion Capture

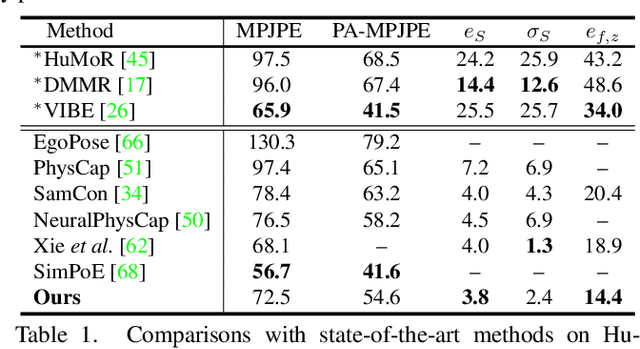
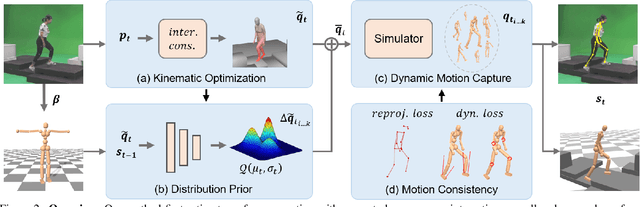
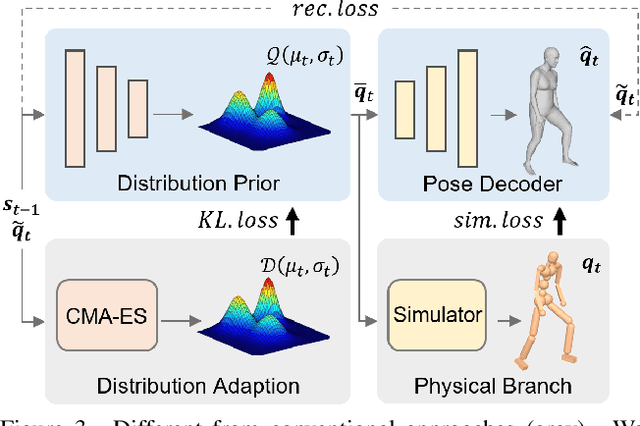
Due to the visual ambiguity, purely kinematic formulations on monocular human motion capture are often physically incorrect, biomechanically implausible, and can not reconstruct accurate interactions. In this work, we focus on exploiting the high-precision and non-differentiable physics simulator to incorporate dynamical constraints in motion capture. Our key-idea is to use real physical supervisions to train a target pose distribution prior for sampling-based motion control to capture physically plausible human motion. To obtain accurate reference motion with terrain interactions for the sampling, we first introduce an interaction constraint based on SDF (Signed Distance Field) to enforce appropriate ground contact modeling. We then design a novel two-branch decoder to avoid stochastic error from pseudo ground-truth and train a distribution prior with the non-differentiable physics simulator. Finally, we regress the sampling distribution from the current state of the physical character with the trained prior and sample satisfied target poses to track the estimated reference motion. Qualitative and quantitative results show that we can obtain physically plausible human motion with complex terrain interactions, human shape variations, and diverse behaviors. More information can be found at~\url{https://www.yangangwang.com/papers/HBZ-NM-2022-03.html}

Automatic Item Generation of Figural Analogy Problems: A Review and Outlook

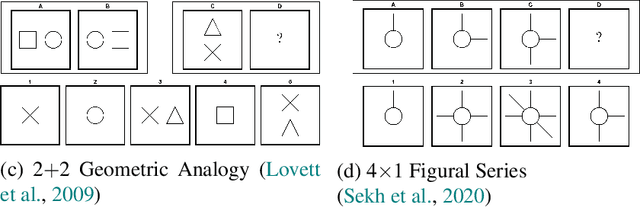
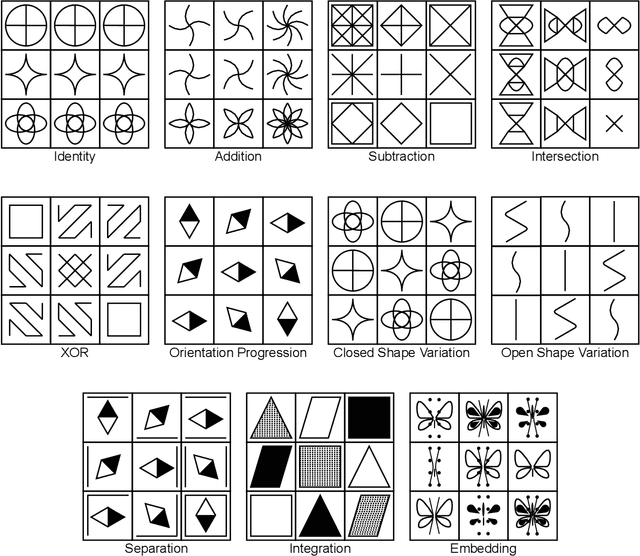
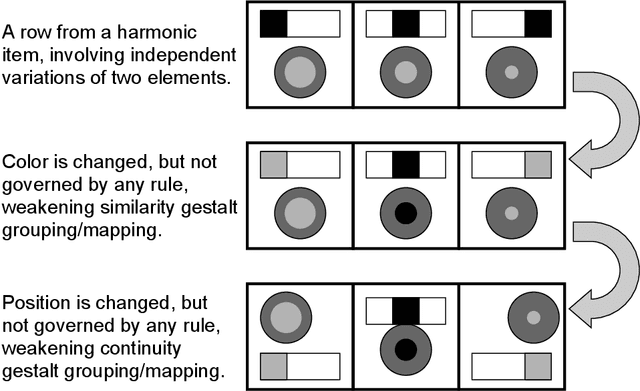
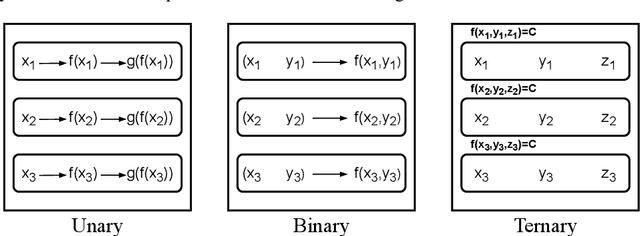
Figural analogy problems have long been a widely used format in human intelligence tests. In the past four decades, more and more research has investigated automatic item generation for figural analogy problems, i.e., algorithmic approaches for systematically and automatically creating such problems. In cognitive science and psychometrics, this research can deepen our understandings of human analogical ability and psychometric properties of figural analogies. With the recent development of data-driven AI models for reasoning about figural analogies, the territory of automatic item generation of figural analogies has further expanded. This expansion brings new challenges as well as opportunities, which demand reflection on previous item generation research and planning future studies. This paper reviews the important works of automatic item generation of figural analogies for both human intelligence tests and data-driven AI models. From an interdisciplinary perspective, the principles and technical details of these works are analyzed and compared, and desiderata for future research are suggested.

Learning Time Series from Scale Information

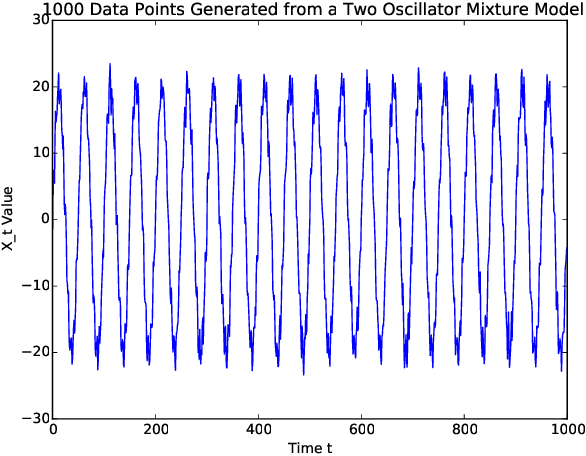
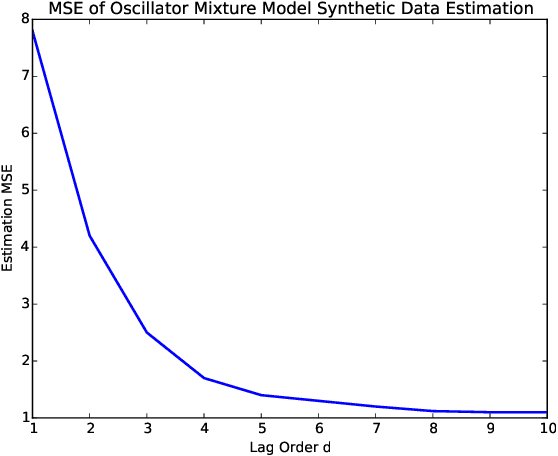
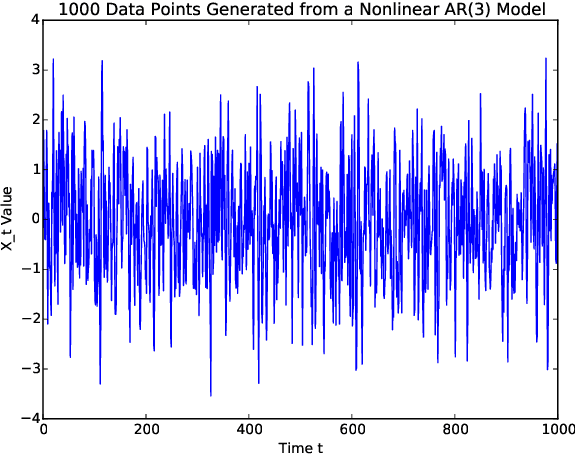
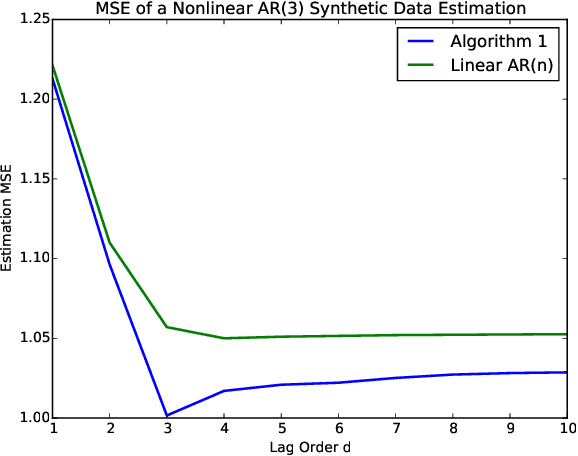
Sequentially obtained dataset usually exhibits different behavior at different data resolutions/scales. Instead of inferring from data at each scale individually, it is often more informative to interpret the data as an ensemble of time series from different scales. This naturally motivated us to propose a new concept referred to as the scale-based inference. The basic idea is that more accurate prediction can be made by exploiting scale information of a time series. We first propose a nonparametric predictor based on $k$-nearest neighbors with an optimally chosen $k$ for a single time series. Based on that, we focus on a specific but important type of scale information, the resolution/sampling rate of time series data. We then propose an algorithm to sequentially predict time series using past data at various resolutions. We prove that asymptotically the algorithm produces the mean prediction error that is no larger than the best possible algorithm at any single resolution, under some optimally chosen parameters. Finally, we establish the general formulations for scale inference, and provide further motivating examples. Experiments on both synthetic and real data illustrate the potential applicability of our approaches to a wide range of time series models.

Multi-Phase Locking Value: A Generalized Method for Determining Instantaneous Multi-frequency Phase Coupling

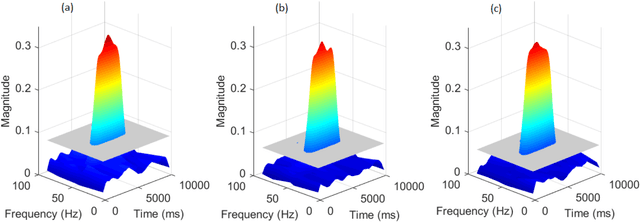
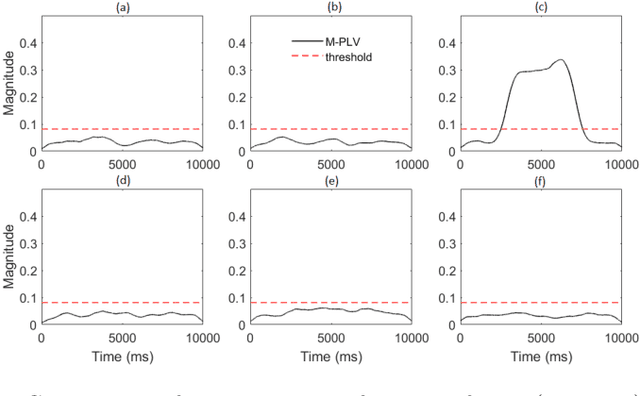
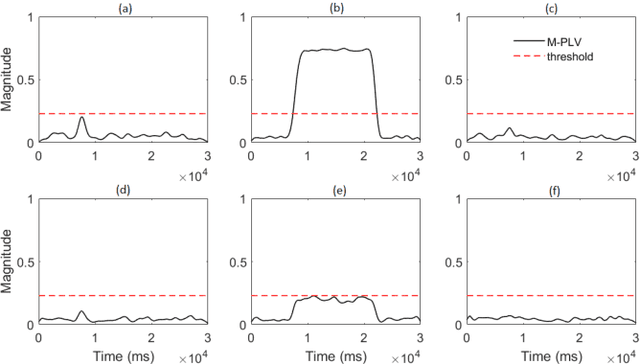
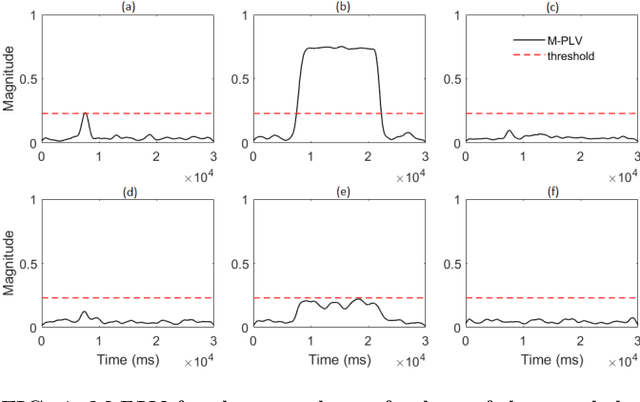
Many physical, biological and neural systems behave as coupled oscillators, with characteristic phase coupling across different frequencies. Methods such as $n:m$ phase locking value and bi-phase locking value have previously been proposed to quantify phase coupling between two resonant frequencies (e.g. $f$, $2f/3$) and across three frequencies (e.g. $f_1$, $f_2$, $f_1+f_2$), respectively. However, the existing phase coupling metrics have their limitations and limited applications. They cannot be used to detect or quantify phase coupling across multiple frequencies (e.g. $f_1$, $f_2$, $f_3$, $f_4$, $f_1+f_2+f_3-f_4$), or coupling that involves non-integer multiples of the frequencies (e.g. $f_1$, $f_2$, $2f_1/3+f_2/3$). To address the gap, this paper proposes a generalized approach, named multi-phase locking value (M-PLV), for the quantification of various types of instantaneous multi-frequency phase coupling. Different from most instantaneous phase coupling metrics that measure the simultaneous phase coupling, the proposed M-PLV method also allows the detection of delayed phase coupling and the associated time lag between coupled oscillators. The M-PLV has been tested on cases where synthetic coupled signals are generated using white Gaussian signals, and a system comprised of multiple coupled R\"ossler oscillators. Results indicate that the M-PLV can provide a reliable estimation of the time window and frequency combination where the phase coupling is significant, as well as a precise determination of time lag in the case of delayed coupling. This method has the potential to become a powerful new tool for exploring phase coupling in complex nonlinear dynamic systems.