Near-Optimal Offline Reinforcement Learning via Double Variance Reduction

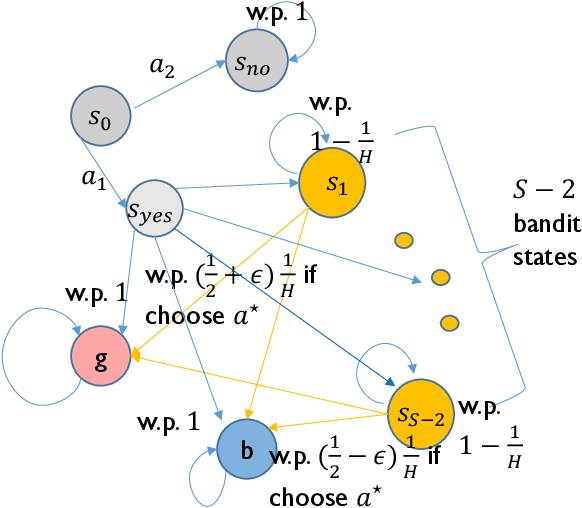
We consider the problem of offline reinforcement learning (RL) -- a well-motivated setting of RL that aims at policy optimization using only historical data. Despite its wide applicability, theoretical understandings of offline RL, such as its optimal sample complexity, remain largely open even in basic settings such as \emph{tabular} Markov Decision Processes (MDPs). In this paper, we propose Off-Policy Double Variance Reduction (OPDVR), a new variance reduction based algorithm for offline RL. Our main result shows that OPDVR provably identifies an $\epsilon$-optimal policy with $\widetilde{O}(H^2/d_m\epsilon^2)$ episodes of offline data in the finite-horizon stationary transition setting, where $H$ is the horizon length and $d_m$ is the minimal marginal state-action distribution induced by the behavior policy. This improves over the best known upper bound by a factor of $H$. Moreover, we establish an information-theoretic lower bound of $\Omega(H^2/d_m\epsilon^2)$ which certifies that OPDVR is optimal up to logarithmic factors. Lastly, we show that OPDVR also achieves rate-optimal sample complexity under alternative settings such as the finite-horizon MDPs with non-stationary transitions and the infinite horizon MDPs with discounted rewards.

An Optimal Reduction of TV-Denoising to Adaptive Online Learning

We consider the problem of estimating a function from $n$ noisy samples whose discrete Total Variation (TV) is bounded by $C_n$. We reveal a deep connection to the seemingly disparate problem of Strongly Adaptive online learning (Daniely et al, 2015) and provide an $O(n \log n)$ time algorithm that attains the near minimax optimal rate of $\tilde O (n^{1/3}C_n^{2/3})$ under squared error loss. The resulting algorithm runs online and optimally adapts to the unknown smoothness parameter $C_n$. This leads to a new and more versatile alternative to wavelets-based methods for (1) adaptively estimating TV bounded functions; (2) online forecasting of TV bounded trends in time series.

Revisiting Model-Agnostic Private Learning: Faster Rates and Active Learning

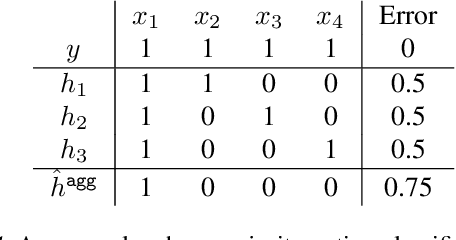
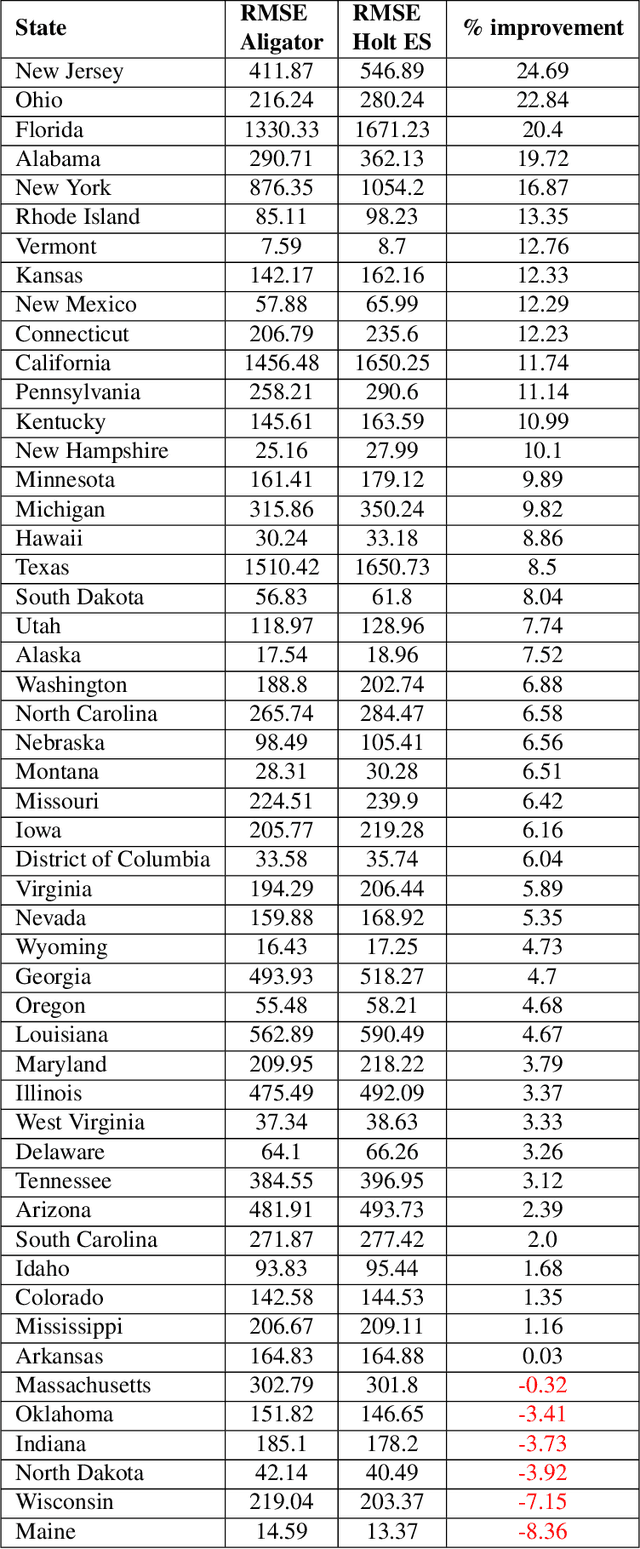
The Private Aggregation of Teacher Ensembles (PATE) framework is one of the most promising recent approaches in differentially private learning. Existing theoretical analysis shows that PATE consistently learns any VC-classes in the realizable setting, but falls short in explaining its success in more general cases where the error rate of the optimal classifier is bounded away from zero. We fill in this gap by introducing the Tsybakov Noise Condition (TNC) and establish stronger and more interpretable learning bounds. These bounds provide new insights into when PATE works and improve over existing results even in the narrower realizable setting. We also investigate the compelling idea of using active learning for saving privacy budget. The novel components in the proofs include a more refined analysis of the majority voting classifier -- which could be of independent interest -- and an observation that the synthetic "student" learning problem is nearly realizable by construction under the Tsybakov noise condition.

Inter-Series Attention Model for COVID-19 Forecasting

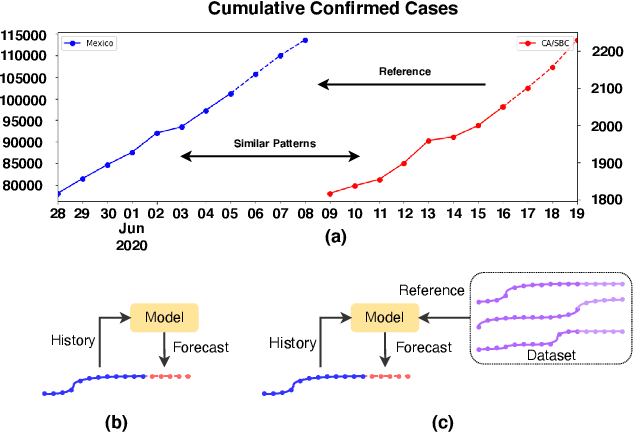
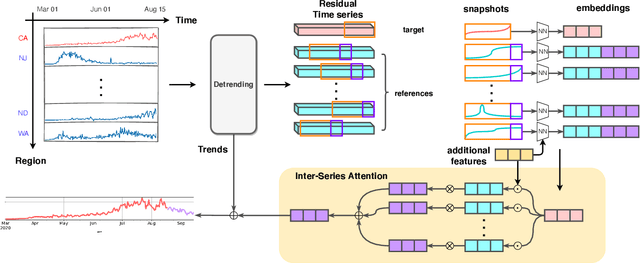
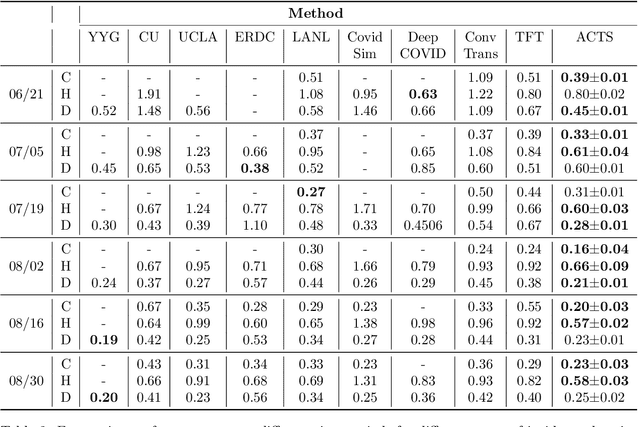
COVID-19 pandemic has an unprecedented impact all over the world since early 2020. During this public health crisis, reliable forecasting of the disease becomes critical for resource allocation and administrative planning. The results from compartmental models such as SIR and SEIR are popularly referred by CDC and news media. With more and more COVID-19 data becoming available, we examine the following question: Can a direct data-driven approach without modeling the disease spreading dynamics outperform the well referred compartmental models and their variants? In this paper, we show the possibility. It is observed that as COVID-19 spreads at different speed and scale in different geographic regions, it is highly likely that similar progression patterns are shared among these regions within different time periods. This intuition lead us to develop a new neural forecasting model, called Attention Crossing Time Series (\textbf{ACTS}), that makes forecasts via comparing patterns across time series obtained from multiple regions. The attention mechanism originally developed for natural language processing can be leveraged and generalized to materialize this idea. Among 13 out of 18 testings including forecasting newly confirmed cases, hospitalizations and deaths, \textbf{ACTS} outperforms all the leading COVID-19 forecasters highlighted by CDC.

Voting-based Approaches For Differentially Private Federated Learning

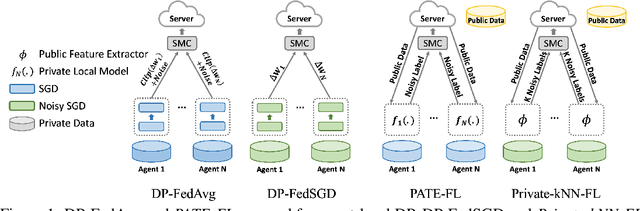
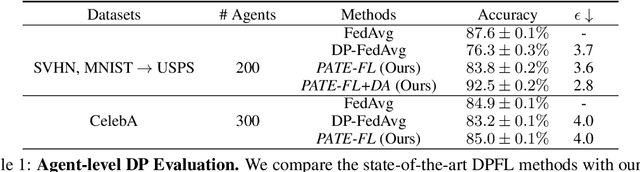
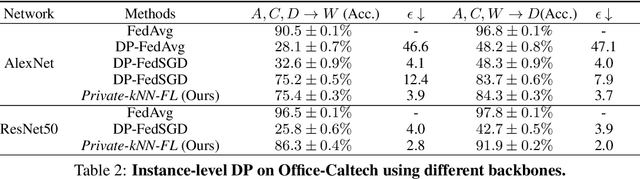
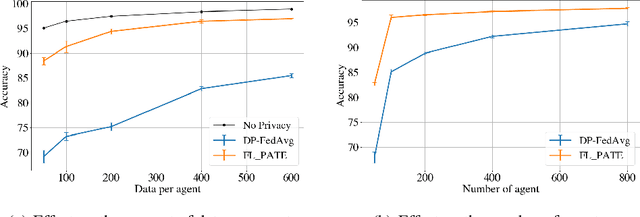
While federated learning (FL) enables distributed agents to collaboratively train a centralized model without sharing data with each other, it fails to protect users against inference attacks that mine private information from the centralized model. Thus, facilitating federated learning methods with differential privacy (DPFL) becomes attractive. Existing algorithms based on privately aggregating clipped gradients require many rounds of communication, which may not converge, and cannot scale up to large-capacity models due to explicit dimension-dependence in its added noise. In this paper, we adopt the knowledge transfer model of private learning pioneered by Papernot et al. (2017; 2018) and extend their algorithm PATE, as well as the recent alternative PrivateKNN (Zhu et al., 2020) to the federated learning setting. The key difference is that our method privately aggregates the labels from the agents in a voting scheme, instead of aggregating the gradients, hence avoiding the dimension dependence and achieving significant savings in communication cost. Theoretically, we show that when the margins of the voting scores are large, the agents enjoy exponentially higher accuracy and stronger (data-dependent) differential privacy guarantees on both agent-level and instance-level. Extensive experiments show that our approach significantly improves the privacy-utility trade-off over the current state-of-the-art in DPFL.

Adaptive Online Estimation of Piecewise Polynomial Trends

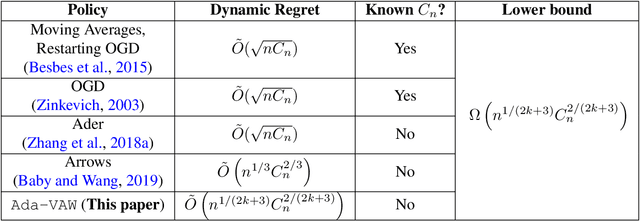
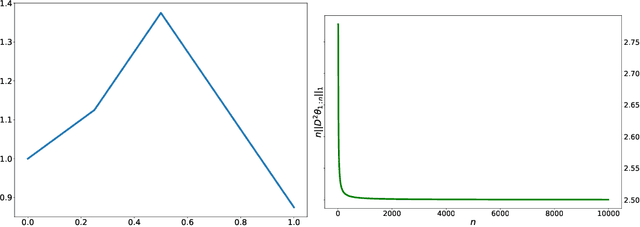
We consider the framework of non-stationary stochastic optimization [Besbes et al, 2015] with squared error losses and noisy gradient feedback where the dynamic regret of an online learner against a time varying comparator sequence is studied. Motivated from the theory of non-parametric regression, we introduce a new variational constraint that enforces the comparator sequence to belong to a discrete $k^{th}$ order Total Variation ball of radius $C_n$. This variational constraint models comparators that have piece-wise polynomial structure which has many relevant practical applications [Tibshirani, 2014]. By establishing connections to the theory of wavelet based non-parametric regression, we design a polynomial time algorithm that achieves the nearly optimal dynamic regret of $\tilde{O}(n^{\frac{1}{2k+3}}C_n^{\frac{2}{2k+3}})$. The proposed policy is adaptive to the unknown radius $C_n$. Further, we show that the same policy is minimax optimal for several other non-parametric families of interest.

Near Optimal Provable Uniform Convergence in Off-Policy Evaluation for Reinforcement Learning

The Off-Policy Evaluation aims at estimating the performance of target policy $\pi$ using offline data rolled in by a logging policy $\mu$. Intensive studies have been conducted and the recent marginalized importance sampling (MIS) achieves the sample efficiency for OPE. However, it is rarely known if uniform convergence guarantees in OPE can be obtained efficiently. In this paper, we consider this new question and reveal the comprehensive relationship between OPE and offline learning for the first time. For the global policy class, by using the fully model-based OPE estimator, our best result is able to achieve $\epsilon$-uniform convergence with complexity $\widetilde{O}(H^3\cdot\min(S,H)/d_m\epsilon^2)$, where $d_m$ is an instance-dependent quantity decided by $\mu$. This result is only one factor away from our uniform convergence lower bound up to a logarithmic factor. For the local policy class, $\epsilon$-uniform convergence is achieved with the optimal complexity $\widetilde{O}(H^3/d_m\epsilon^2)$ in the off-policy setting. This result complements the work of sparse model-based planning (Agarwal et al. 2019) with generative model. Lastly, one interesting corollary of our intermediate result implies a refined analysis over simulation lemma.

Bullseye Polytope: A Scalable Clean-Label Poisoning Attack with Improved Transferability

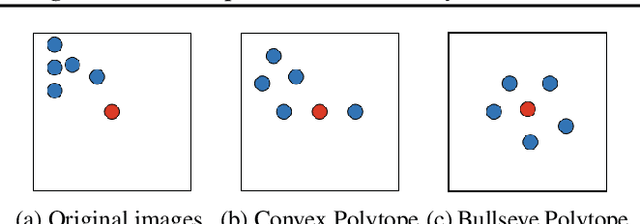
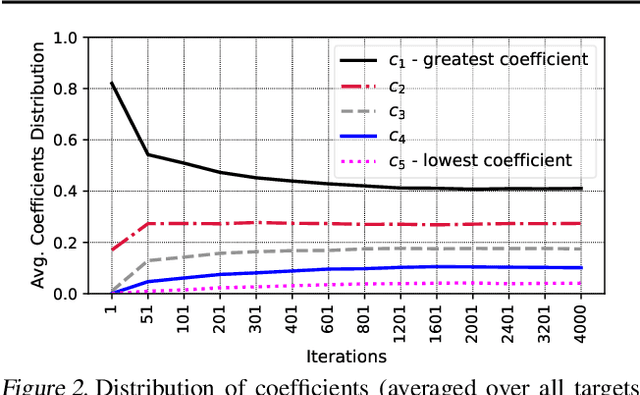
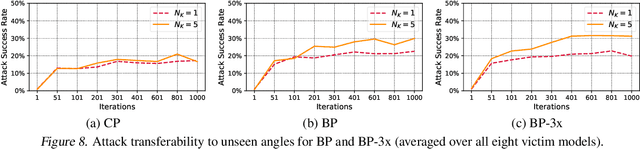
A recent source of concern for the security of neural networks is the emergence of clean-label dataset poisoning attacks, wherein correctly labeled poisoned samples are injected in the training dataset. While these poisons look legitimate to the human observer, they contain malicious characteristics that trigger a targeted misclassification during inference. We propose a scalable and transferable clean-label attack, Bullseye Polytope, which creates poison images centered around the target image in the feature space. Bullseye Polytope improves the attack success rate of the current state-of-the-art by 26.75% in end-to-end training, while increasing attack speed by a factor of 12. We further extend Bullseye Polytope to a more practical attack model by including multiple images of the same object (e.g., from different angles) in crafting the poisoned samples. We demonstrate that this extension improves attack transferability by over 16% to unseen images (of the same object) without increasing the number of poisons.

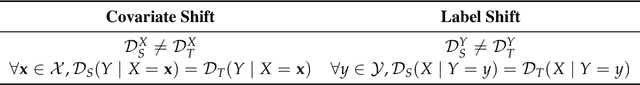
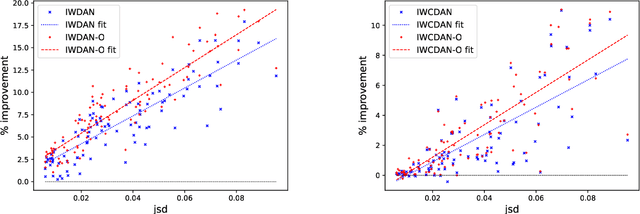
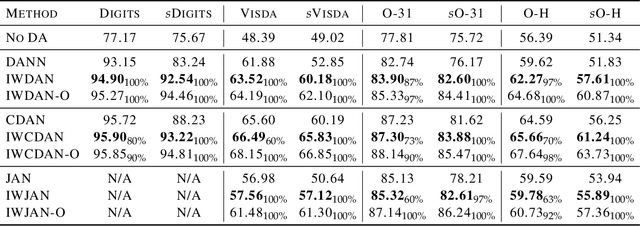
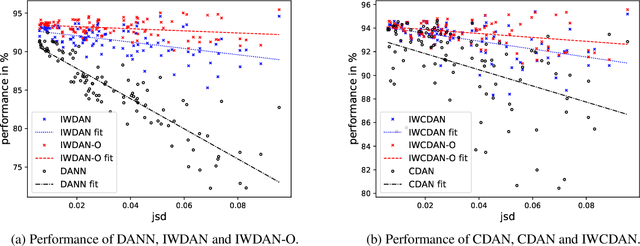
Domain Adaptation with Conditional Distribution Matching and Generalized Label Shift

Adversarial learning has demonstrated good performance in the unsupervised domain adaptation setting, by learning domain-invariant representations that perform well on the source domain. However, recent work has underlined limitations of existing methods in the presence of mismatched label distributions between the source and target domains. In this paper, we extend a recent upper-bound on the performance of adversarial domain adaptation to multi-class classification and more general discriminators. We then propose generalized label shift (GLS) as a way to improve robustness against mismatched label distributions. GLS states that, conditioned on the label, there exists a representation of the input that is invariant between the source and target domains. Under GLS, we provide theoretical guarantees on the transfer performance of any classifier. We also devise necessary and sufficient conditions for GLS to hold. The conditions are based on the estimation of the relative class weights between domains and on an appropriate reweighting of samples. Guided by our theoretical insights, we modify three widely used algorithms, JAN, DANN and CDAN and evaluate their performance on standard domain adaptation tasks where our method outperforms the base versions. We also demonstrate significant gains on artificially created tasks with large divergences between their source and target label distributions.

Asymptotically Efficient Off-Policy Evaluation for Tabular Reinforcement Learning

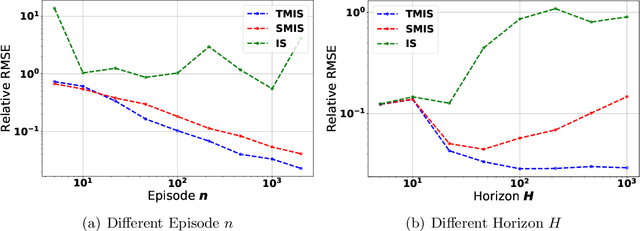
We consider the problem of off-policy evaluation for reinforcement learning, where the goal is to estimate the expected reward of a target policy $\pi$ using offline data collected by running a logging policy $\mu$. Standard importance-sampling based approaches for this problem suffer from a variance that scales exponentially with time horizon $H$, which motivates a splurge of recent interest in alternatives that break the "Curse of Horizon" (Liu et al. 2018, Xie et al. 2019). In particular, it was shown that a marginalized importance sampling (MIS) approach can be used to achieve an estimation error of order $O(H^3/ n)$ in mean square error (MSE) under an episodic Markov Decision Process model with finite states and potentially infinite actions. The MSE bound however is still a factor of $H$ away from a Cramer-Rao lower bound of order $\Omega(H^2/n)$. In this paper, we prove that with a simple modification to the MIS estimator, we can asymptotically attain the Cramer-Rao lower bound, provided that the action space is finite. We also provide a general method for constructing MIS estimators with high-probability error bounds.