Yu-Xiang Wang
University of California Santa Barbara
Sample-Efficient Reinforcement Learning with loglog Switching Cost
Feb 13, 2022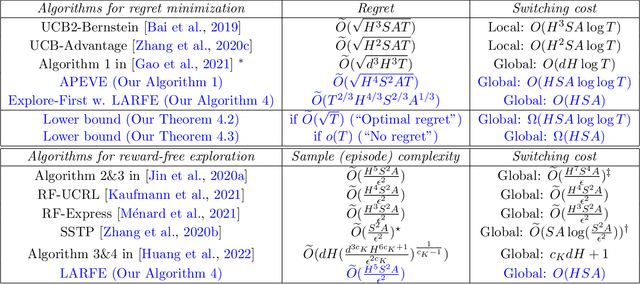
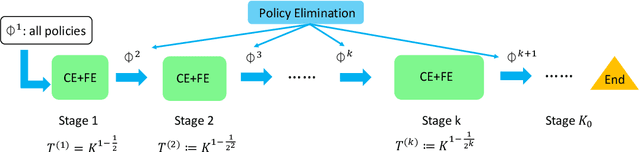
Abstract:We study the problem of reinforcement learning (RL) with low (policy) switching cost - a problem well-motivated by real-life RL applications in which deployments of new policies are costly and the number of policy updates must be low. In this paper, we propose a new algorithm based on stage-wise exploration and adaptive policy elimination that achieves a regret of $\widetilde{O}(\sqrt{H^4S^2AT})$ while requiring a switching cost of $O(HSA \log\log T)$. This is an exponential improvement over the best-known switching cost $O(H^2SA\log T)$ among existing methods with $\widetilde{O}(\mathrm{poly}(H,S,A)\sqrt{T})$ regret. In the above, $S,A$ denotes the number of states and actions in an $H$-horizon episodic Markov Decision Process model with unknown transitions, and $T$ is the number of steps. We also prove an information-theoretical lower bound which says that a switching cost of $\Omega(HSA)$ is required for any no-regret algorithm. As a byproduct, our new algorithmic techniques allow us to derive a \emph{reward-free} exploration algorithm with an optimal switching cost of $O(HSA)$.
Towards Agnostic Feature-based Dynamic Pricing: Linear Policies vs Linear Valuation with Unknown Noise
Jan 27, 2022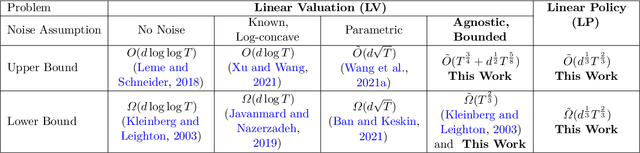
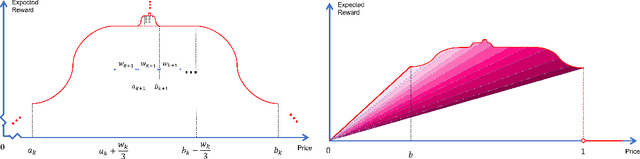
Abstract:In feature-based dynamic pricing, a seller sets appropriate prices for a sequence of products (described by feature vectors) on the fly by learning from the binary outcomes of previous sales sessions ("Sold" if valuation $\geq$ price, and "Not Sold" otherwise). Existing works either assume noiseless linear valuation or precisely-known noise distribution, which limits the applicability of those algorithms in practice when these assumptions are hard to verify. In this work, we study two more agnostic models: (a) a "linear policy" problem where we aim at competing with the best linear pricing policy while making no assumptions on the data, and (b) a "linear noisy valuation" problem where the random valuation is linear plus an unknown and assumption-free noise. For the former model, we show a $\tilde{\Theta}(d^{\frac13}T^{\frac23})$ minimax regret up to logarithmic factors. For the latter model, we present an algorithm that achieves an $\tilde{O}(T^{\frac34})$ regret, and improve the best-known lower bound from $\Omega(T^{\frac35})$ to $\tilde{\Omega}(T^{\frac23})$. These results demonstrate that no-regret learning is possible for feature-based dynamic pricing under weak assumptions, but also reveal a disappointing fact that the seemingly richer pricing feedback is not significantly more useful than the bandit-feedback in regret reduction.
Optimal Dynamic Regret in Proper Online Learning with Strongly Convex Losses and Beyond
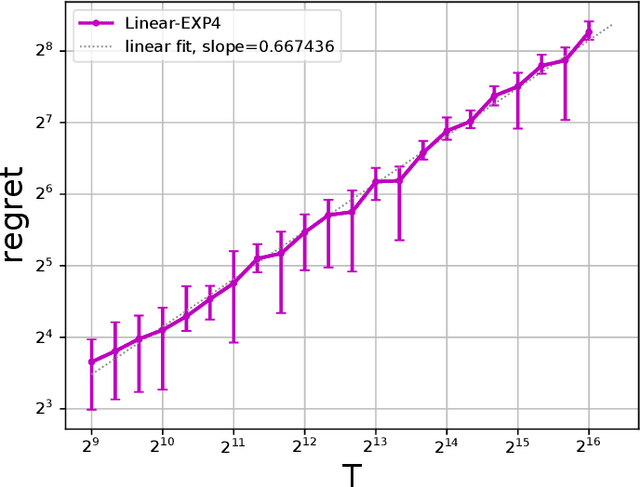
Jan 21, 2022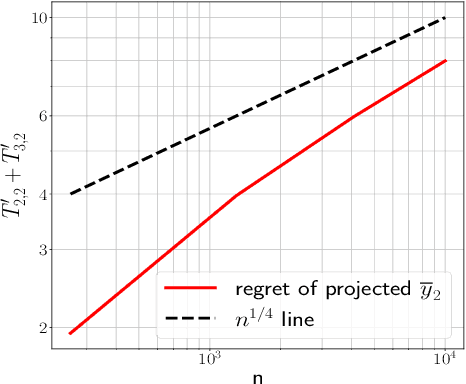


Abstract:We study the framework of universal dynamic regret minimization with strongly convex losses. We answer an open problem in Baby and Wang 2021 by showing that in a proper learning setup, Strongly Adaptive algorithms can achieve the near optimal dynamic regret of $\tilde O(d^{1/3} n^{1/3}\text{TV}[u_{1:n}]^{2/3} \vee d)$ against any comparator sequence $u_1,\ldots,u_n$ simultaneously, where $n$ is the time horizon and $\text{TV}[u_{1:n}]$ is the Total Variation of comparator. These results are facilitated by exploiting a number of new structures imposed by the KKT conditions that were not considered in Baby and Wang 2021 which also lead to other improvements over their results such as: (a) handling non-smooth losses and (b) improving the dimension dependence on regret. Further, we also derive near optimal dynamic regret rates for the special case of proper online learning with exp-concave losses and an $L_\infty$ constrained decision set.
Multivariate Trend Filtering for Lattice Data
Dec 29, 2021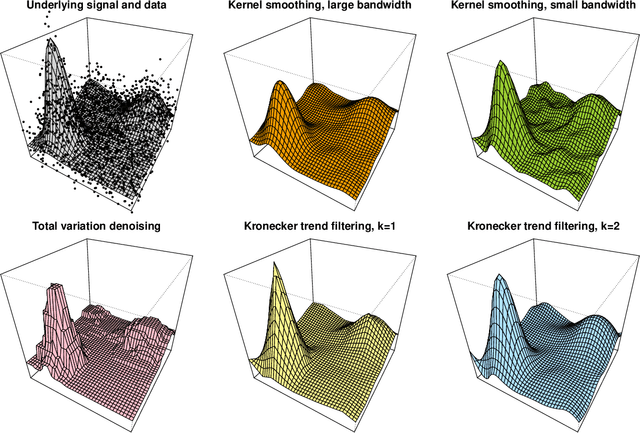
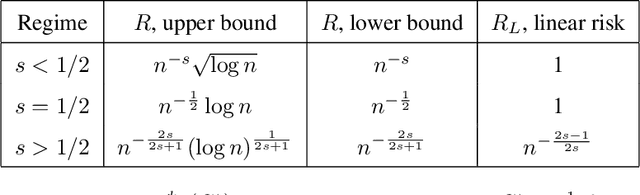
Abstract:We study a multivariate version of trend filtering, called Kronecker trend filtering or KTF, for the case in which the design points form a lattice in $d$ dimensions. KTF is a natural extension of univariate trend filtering (Steidl et al., 2006; Kim et al., 2009; Tibshirani, 2014), and is defined by minimizing a penalized least squares problem whose penalty term sums the absolute (higher-order) differences of the parameter to be estimated along each of the coordinate directions. The corresponding penalty operator can be written in terms of Kronecker products of univariate trend filtering penalty operators, hence the name Kronecker trend filtering. Equivalently, one can view KTF in terms of an $\ell_1$-penalized basis regression problem where the basis functions are tensor products of falling factorial functions, a piecewise polynomial (discrete spline) basis that underlies univariate trend filtering. This paper is a unification and extension of the results in Sadhanala et al. (2016, 2017). We develop a complete set of theoretical results that describe the behavior of $k^{\mathrm{th}}$ order Kronecker trend filtering in $d$ dimensions, for every $k \geq 0$ and $d \geq 1$. This reveals a number of interesting phenomena, including the dominance of KTF over linear smoothers in estimating heterogeneously smooth functions, and a phase transition at $d=2(k+1)$, a boundary past which (on the high dimension-to-smoothness side) linear smoothers fail to be consistent entirely. We also leverage recent results on discrete splines from Tibshirani (2020), in particular, discrete spline interpolation results that enable us to extend the KTF estimate to any off-lattice location in constant-time (independent of the size of the lattice $n$).
Privately Publishable Per-instance Privacy
Nov 03, 2021
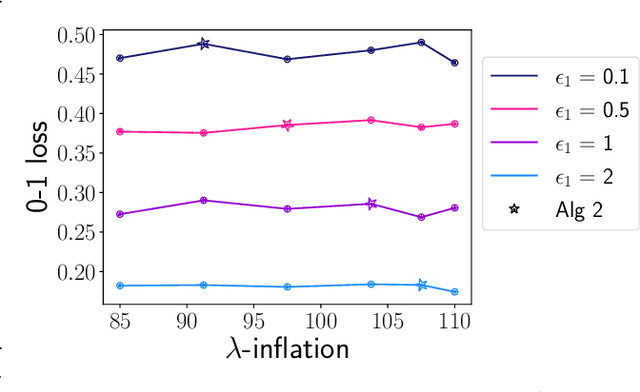
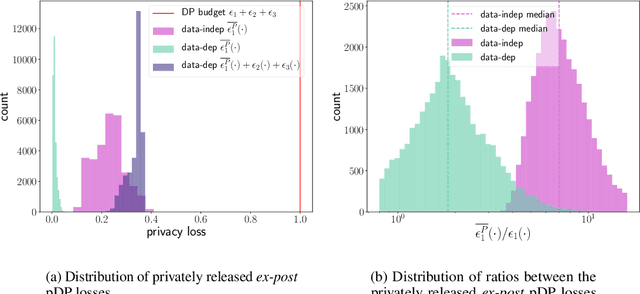
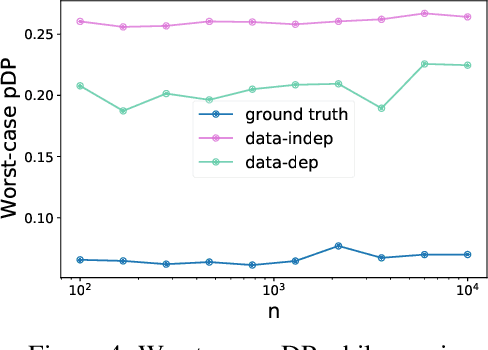
Abstract:We consider how to privately share the personalized privacy losses incurred by objective perturbation, using per-instance differential privacy (pDP). Standard differential privacy (DP) gives us a worst-case bound that might be orders of magnitude larger than the privacy loss to a particular individual relative to a fixed dataset. The pDP framework provides a more fine-grained analysis of the privacy guarantee to a target individual, but the per-instance privacy loss itself might be a function of sensitive data. In this paper, we analyze the per-instance privacy loss of releasing a private empirical risk minimizer learned via objective perturbation, and propose a group of methods to privately and accurately publish the pDP losses at little to no additional privacy cost.
Towards Instance-Optimal Offline Reinforcement Learning with Pessimism
Oct 17, 2021

Abstract:We study the offline reinforcement learning (offline RL) problem, where the goal is to learn a reward-maximizing policy in an unknown Markov Decision Process (MDP) using the data coming from a policy $\mu$. In particular, we consider the sample complexity problems of offline RL for finite-horizon MDPs. Prior works study this problem based on different data-coverage assumptions, and their learning guarantees are expressed by the covering coefficients which lack the explicit characterization of system quantities. In this work, we analyze the Adaptive Pessimistic Value Iteration (APVI) algorithm and derive the suboptimality upper bound that nearly matches \[ O\left(\sum_{h=1}^H\sum_{s_h,a_h}d^{\pi^\star}_h(s_h,a_h)\sqrt{\frac{\mathrm{Var}_{P_{s_h,a_h}}{(V^\star_{h+1}+r_h)}}{d^\mu_h(s_h,a_h)}}\sqrt{\frac{1}{n}}\right). \] In complementary, we also prove a per-instance information-theoretical lower bound under the weak assumption that $d^\mu_h(s_h,a_h)>0$ if $d^{\pi^\star}_h(s_h,a_h)>0$. Different from the previous minimax lower bounds, the per-instance lower bound (via local minimaxity) is a much stronger criterion as it applies to individual instances separately. Here $\pi^\star$ is a optimal policy, $\mu$ is the behavior policy and $d_h^\mu$ is the marginal state-action probability. We call the above equation the intrinsic offline reinforcement learning bound since it directly implies all the existing optimal results: minimax rate under uniform data-coverage assumption, horizon-free setting, single policy concentrability, and the tight problem-dependent results. Later, we extend the result to the assumption-free regime (where we make no assumption on $ \mu$) and obtain the assumption-free intrinsic bound. Due to its generic form, we believe the intrinsic bound could help illuminate what makes a specific problem hard and reveal the fundamental challenges in offline RL.
Optimal Accounting of Differential Privacy via Characteristic Function
Jun 16, 2021
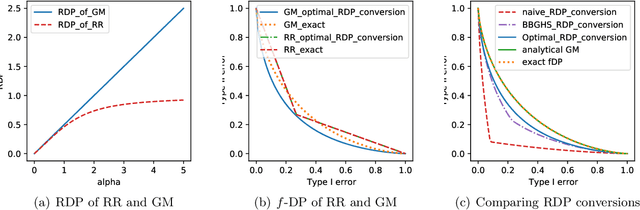

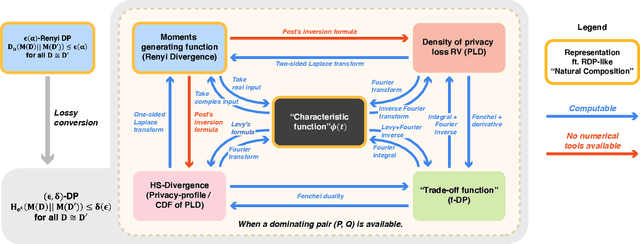
Abstract:Characterizing the privacy degradation over compositions, i.e., privacy accounting, is a fundamental topic in differential privacy (DP) with many applications to differentially private machine learning and federated learning. We propose a unification of recent advances (Renyi DP, privacy profiles, $f$-DP and the PLD formalism) via the characteristic function ($\phi$-function) of a certain ``worst-case'' privacy loss random variable. We show that our approach allows natural adaptive composition like Renyi DP, provides exactly tight privacy accounting like PLD, and can be (often losslessly) converted to privacy profile and $f$-DP, thus providing $(\epsilon,\delta)$-DP guarantees and interpretable tradeoff functions. Algorithmically, we propose an analytical Fourier accountant that represents the complex logarithm of $\phi$-functions symbolically and uses Gaussian quadrature for numerical computation. On several popular DP mechanisms and their subsampled counterparts, we demonstrate the flexibility and tightness of our approach in theory and experiments.
Optimal Uniform OPE and Model-based Offline Reinforcement Learning in Time-Homogeneous, Reward-Free and Task-Agnostic Settings
May 21, 2021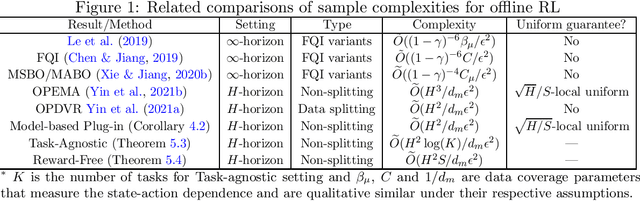
Abstract:This work studies the statistical limits of uniform convergence for offline policy evaluation (OPE) problems with model-based methods (for finite horizon MDP) and provides a unified view towards optimal learning for several well-motivated offline tasks. Uniform OPE $\sup_\Pi|Q^\pi-\hat{Q}^\pi|<\epsilon$ (initiated by \citet{yin2021near}) is a stronger measure than the point-wise (fixed policy) OPE and ensures offline policy learning when $\Pi$ contains all policies (global policy class). In this paper, we establish an $\Omega(H^2 S/d_m\epsilon^2)$ lower bound (over model-based family) for the global uniform OPE, where $d_m$ is the minimal state-action probability induced by the behavior policy. Next, our main result establishes an episode complexity of $\tilde{O}(H^2/d_m\epsilon^2)$ for \emph{local} uniform convergence that applies to all \emph{near-empirically optimal} policies for the MDPs with \emph{stationary} transition. This result implies the optimal sample complexity for offline learning and separates the local uniform OPE from the global case due to the extra $S$ factor. Paramountly, the model-based method combining with our new analysis technique (singleton absorbing MDP) can be adapted to the new settings: offline task-agnostic and the offline reward-free with optimal complexity $\tilde{O}(H^2\log(K)/d_m\epsilon^2)$ ($K$ is the number of tasks) and $\tilde{O}(H^2S/d_m\epsilon^2)$ respectively, which provides a unified framework for simultaneously solving different offline RL problems.
Optimal Dynamic Regret in Exp-Concave Online Learning
Apr 23, 2021
Abstract:We consider the problem of the Zinkevich (2003)-style dynamic regret minimization in online learning with exp-concave losses. We show that whenever improper learning is allowed, a Strongly Adaptive online learner achieves the dynamic regret of $\tilde O(d^{3.5}n^{1/3}C_n^{2/3} \vee d\log n)$ where $C_n$ is the total variation (a.k.a. path length) of the an arbitrary sequence of comparators that may not be known to the learner ahead of time. Achieving this rate was highly nontrivial even for squared losses in 1D where the best known upper bound was $O(\sqrt{nC_n} \vee \log n)$ (Yuan and Lamperski, 2019). Our new proof techniques make elegant use of the intricate structures of the primal and dual variables imposed by the KKT conditions and could be of independent interest. Finally, we apply our results to the classical statistical problem of locally adaptive non-parametric regression (Mammen, 1991; Donoho and Johnstone, 1998) and obtain a stronger and more flexible algorithm that do not require any statistical assumptions or any hyperparameter tuning.
Non-stationary Online Learning with Memory and Non-stochastic Control
Feb 07, 2021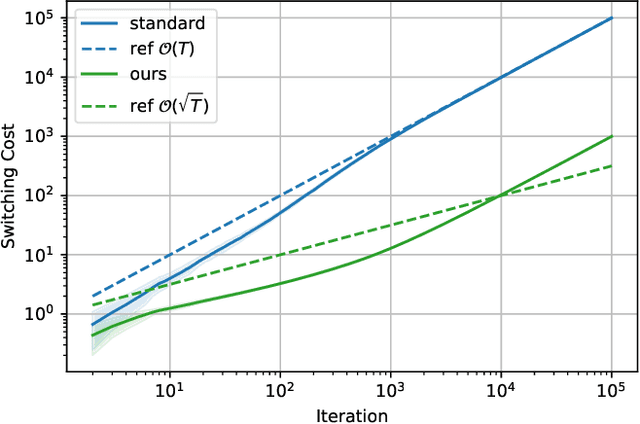
Abstract:We study the problem of Online Convex Optimization (OCO) with memory, which allows loss functions to depend on past decisions and thus captures temporal effects of learning problems. In this paper, we introduce dynamic policy regret as the performance measure to design algorithms robust to non-stationary environments, which competes algorithms' decisions with a sequence of changing comparators. We propose a novel algorithm for OCO with memory that provably enjoys an optimal dynamic policy regret. The key technical challenge is how to control the switching cost, the cumulative movements of player's decisions, which is neatly addressed by a novel decomposition of dynamic policy regret and an appropriate meta-expert structure. Furthermore, we generalize the results to the problem of online non-stochastic control, i.e., controlling a linear dynamical system with adversarial disturbance and convex loss functions. We derive a novel gradient-based controller with dynamic policy regret guarantees, which is the first controller competitive to a sequence of changing policies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge