Self-critical Sequence Training for Image Captioning

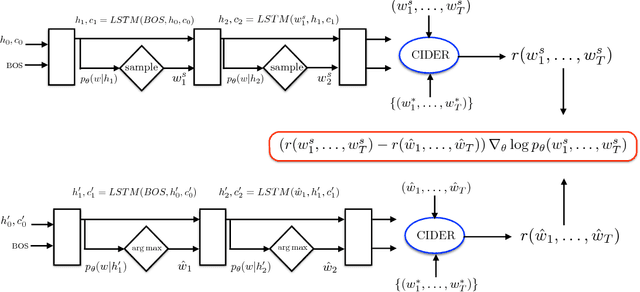
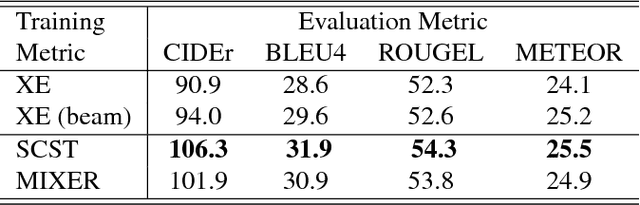
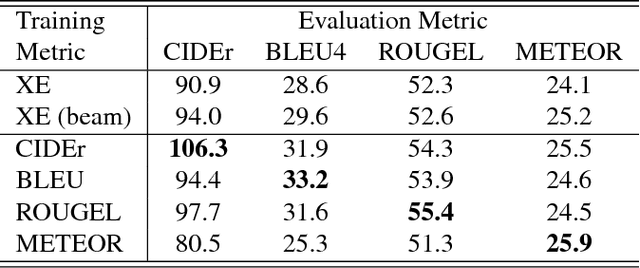
Recently it has been shown that policy-gradient methods for reinforcement learning can be utilized to train deep end-to-end systems directly on non-differentiable metrics for the task at hand. In this paper we consider the problem of optimizing image captioning systems using reinforcement learning, and show that by carefully optimizing our systems using the test metrics of the MSCOCO task, significant gains in performance can be realized. Our systems are built using a new optimization approach that we call self-critical sequence training (SCST). SCST is a form of the popular REINFORCE algorithm that, rather than estimating a "baseline" to normalize the rewards and reduce variance, utilizes the output of its own test-time inference algorithm to normalize the rewards it experiences. Using this approach, estimating the reward signal (as actor-critic methods must do) and estimating normalization (as REINFORCE algorithms typically do) is avoided, while at the same time harmonizing the model with respect to its test-time inference procedure. Empirically we find that directly optimizing the CIDEr metric with SCST and greedy decoding at test-time is highly effective. Our results on the MSCOCO evaluation sever establish a new state-of-the-art on the task, improving the best result in terms of CIDEr from 104.9 to 114.7.

Sobolev GAN

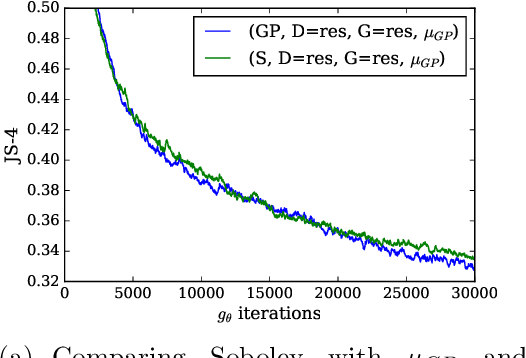
We propose a new Integral Probability Metric (IPM) between distributions: the Sobolev IPM. The Sobolev IPM compares the mean discrepancy of two distributions for functions (critic) restricted to a Sobolev ball defined with respect to a dominant measure $\mu$. We show that the Sobolev IPM compares two distributions in high dimensions based on weighted conditional Cumulative Distribution Functions (CDF) of each coordinate on a leave one out basis. The Dominant measure $\mu$ plays a crucial role as it defines the support on which conditional CDFs are compared. Sobolev IPM can be seen as an extension of the one dimensional Von-Mises Cram\'er statistics to high dimensional distributions. We show how Sobolev IPM can be used to train Generative Adversarial Networks (GANs). We then exploit the intrinsic conditioning implied by Sobolev IPM in text generation. Finally we show that a variant of Sobolev GAN achieves competitive results in semi-supervised learning on CIFAR-10, thanks to the smoothness enforced on the critic by Sobolev GAN which relates to Laplacian regularization.

Fisher GAN

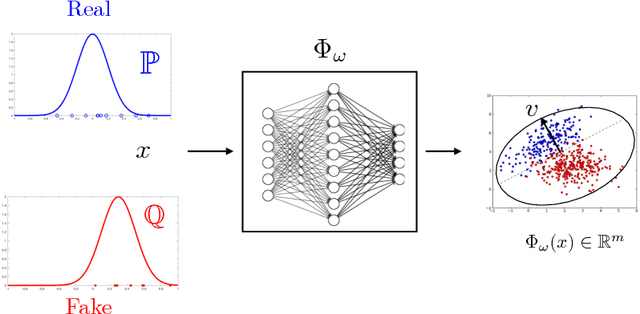
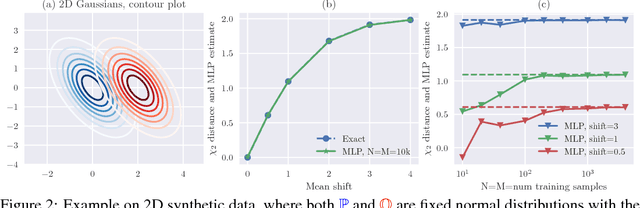
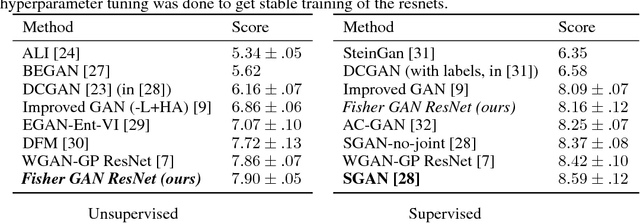
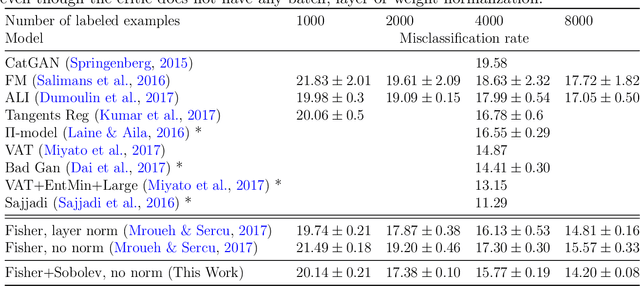
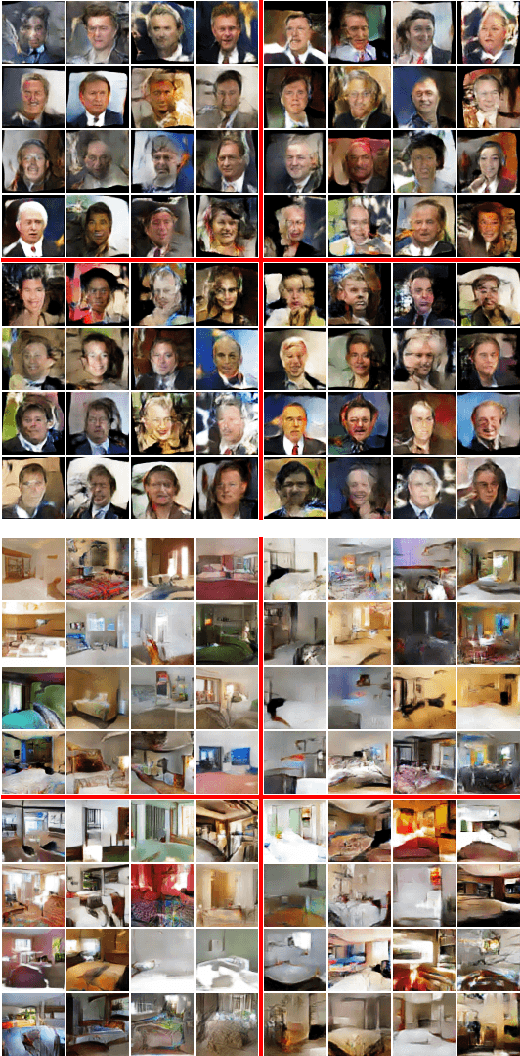
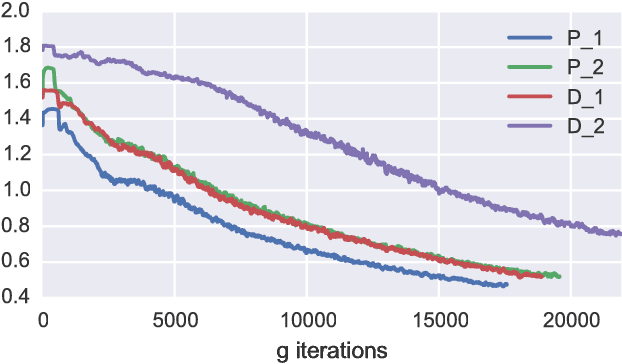
Generative Adversarial Networks (GANs) are powerful models for learning complex distributions. Stable training of GANs has been addressed in many recent works which explore different metrics between distributions. In this paper we introduce Fisher GAN which fits within the Integral Probability Metrics (IPM) framework for training GANs. Fisher GAN defines a critic with a data dependent constraint on its second order moments. We show in this paper that Fisher GAN allows for stable and time efficient training that does not compromise the capacity of the critic, and does not need data independent constraints such as weight clipping. We analyze our Fisher IPM theoretically and provide an algorithm based on Augmented Lagrangian for Fisher GAN. We validate our claims on both image sample generation and semi-supervised classification using Fisher GAN.

McGan: Mean and Covariance Feature Matching GAN

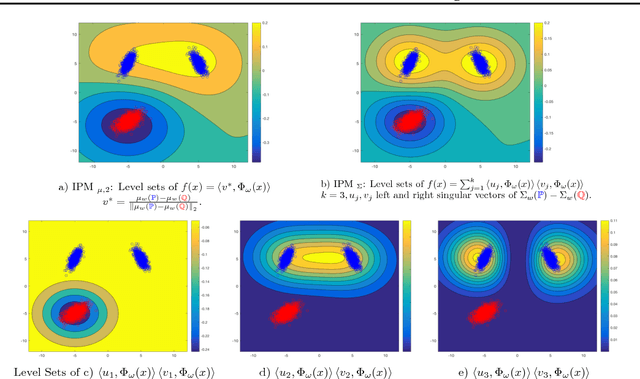
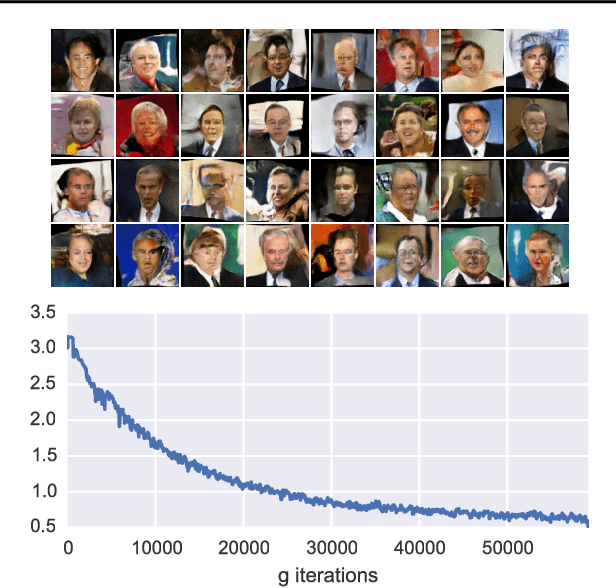
We introduce new families of Integral Probability Metrics (IPM) for training Generative Adversarial Networks (GAN). Our IPMs are based on matching statistics of distributions embedded in a finite dimensional feature space. Mean and covariance feature matching IPMs allow for stable training of GANs, which we will call McGan. McGan minimizes a meaningful loss between distributions.

Local Group Invariant Representations via Orbit Embeddings

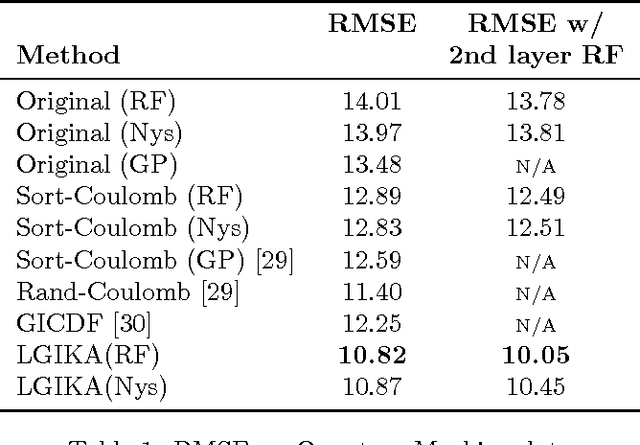
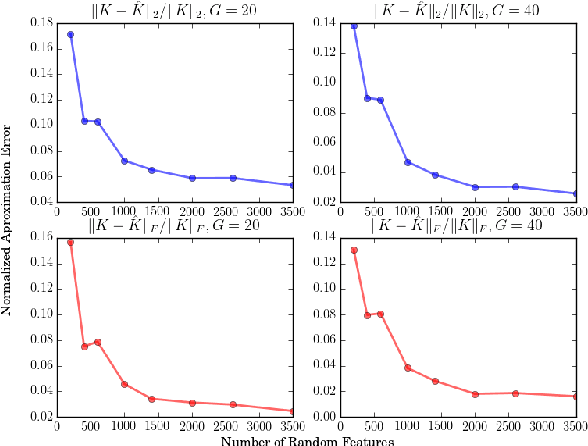
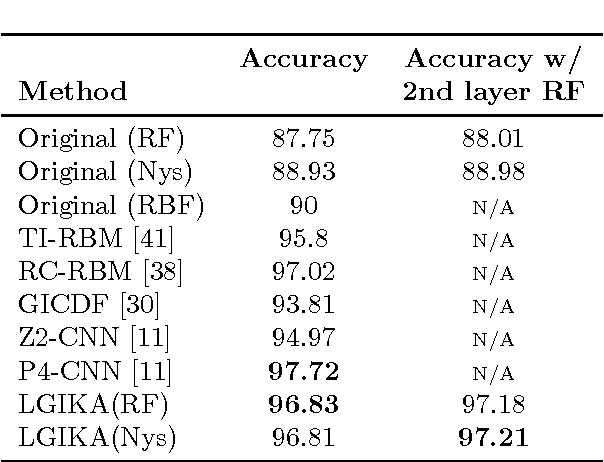
Invariance to nuisance transformations is one of the desirable properties of effective representations. We consider transformations that form a \emph{group} and propose an approach based on kernel methods to derive local group invariant representations. Locality is achieved by defining a suitable probability distribution over the group which in turn induces distributions in the input feature space. We learn a decision function over these distributions by appealing to the powerful framework of kernel methods and generate local invariant random feature maps via kernel approximations. We show uniform convergence bounds for kernel approximation and provide excess risk bounds for learning with these features. We evaluate our method on three real datasets, including Rotated MNIST and CIFAR-10, and observe that it outperforms competing kernel based approaches. The proposed method also outperforms deep CNN on Rotated-MNIST and performs comparably to the recently proposed group-equivariant CNN.

Asymmetrically Weighted CCA And Hierarchical Kernel Sentence Embedding For Image & Text Retrieval

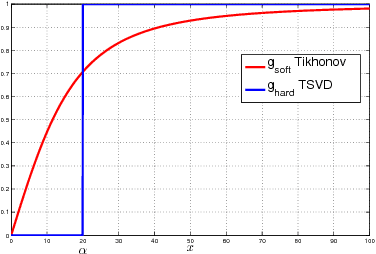
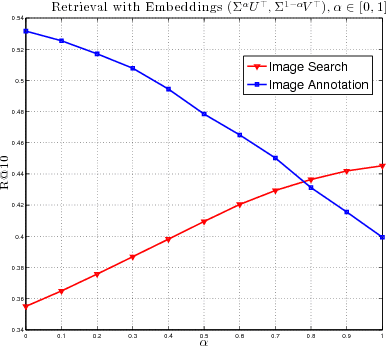
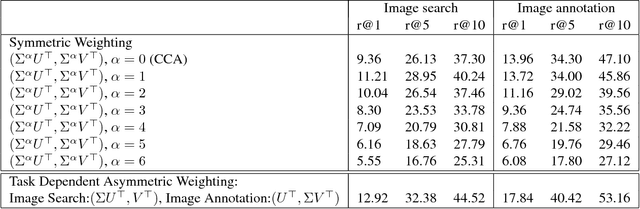
Joint modeling of language and vision has been drawing increasing interest. A multimodal data representation allowing for bidirectional retrieval of images by sentences and vice versa is a key aspect. In this paper we present three contributions in canonical correlation analysis (CCA) based multimodal retrieval. Firstly, we show that an asymmetric weighting of the canonical weights, while achieving a cross view mapping from the search to the query space, improves the retrieval performance. Secondly, we devise a computationally efficient model selection, crucial to generalization and stability, in the framework of the Bj\"ork Golub algorithm for regularized CCA via spectral filtering. Finally, we introduce a Hierarchical Kernel Sentence Embedding (HKSE) that approximates Kernel CCA for a special similarity kernel between distribution of words embedded in a vector space. State of the art results are obtained on MSCOCO and Flickr benchmarks when these three techniques are used in conjunction.

Co-Occuring Directions Sketching for Approximate Matrix Multiply

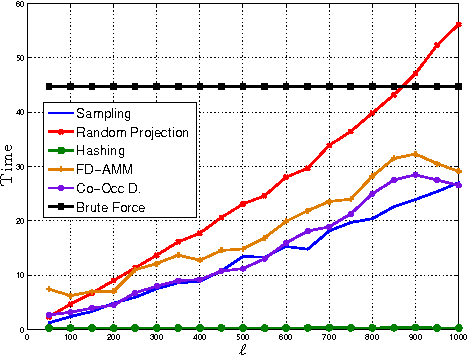
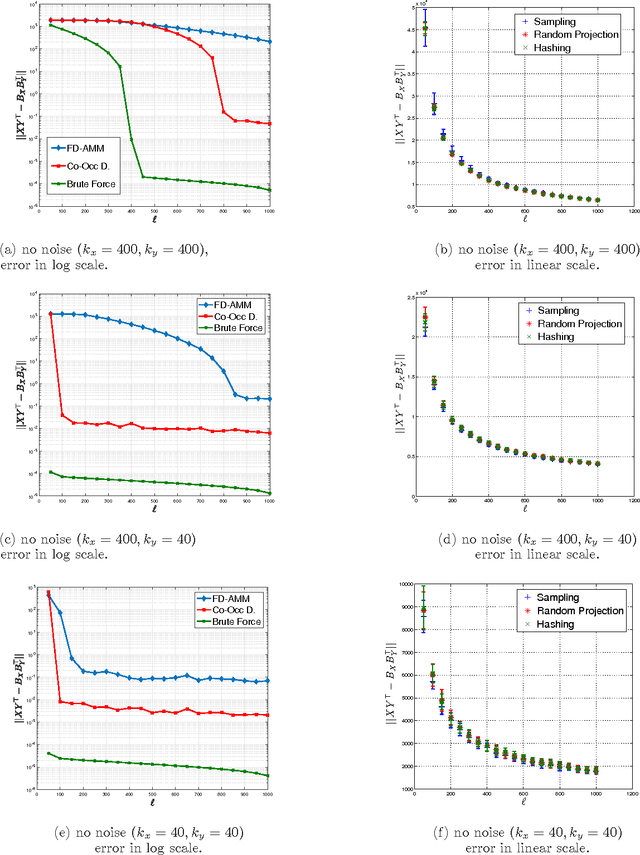
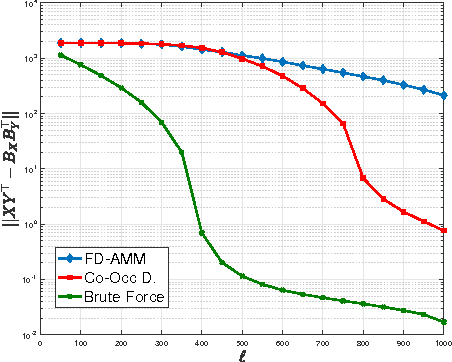
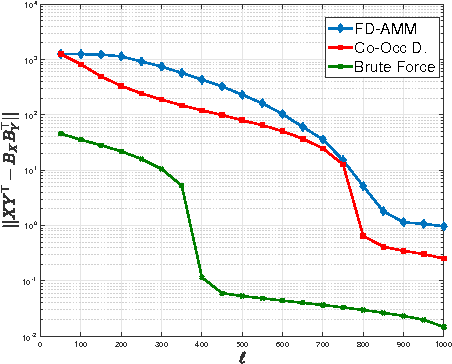
We introduce co-occurring directions sketching, a deterministic algorithm for approximate matrix product (AMM), in the streaming model. We show that co-occuring directions achieves a better error bound for AMM than other randomized and deterministic approaches for AMM. Co-occurring directions gives a $1 + \epsilon$ -approximation of the optimal low rank approximation of a matrix product. Empirically our algorithm outperforms competing methods for AMM, for a small sketch size. We validate empirically our theoretical findings and algorithms

Learning with Group Invariant Features: A Kernel Perspective

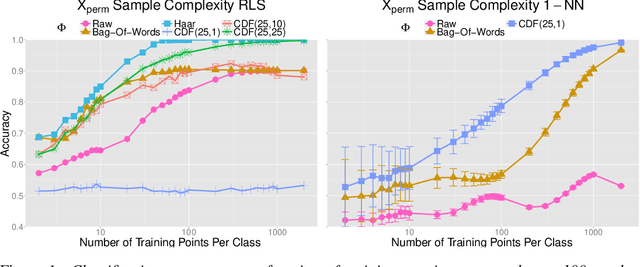
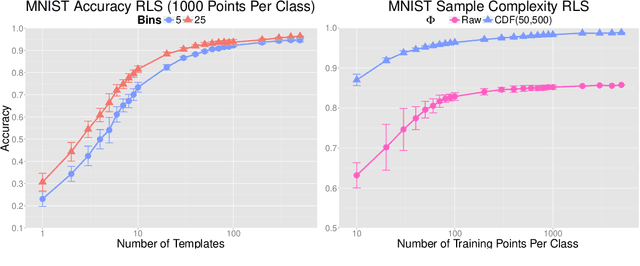
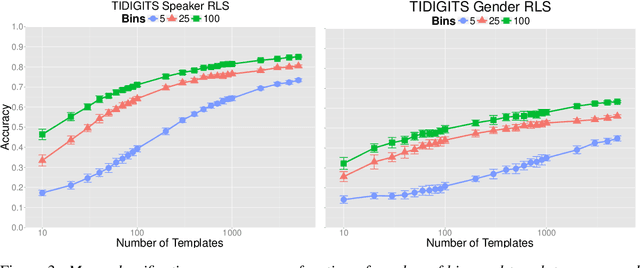
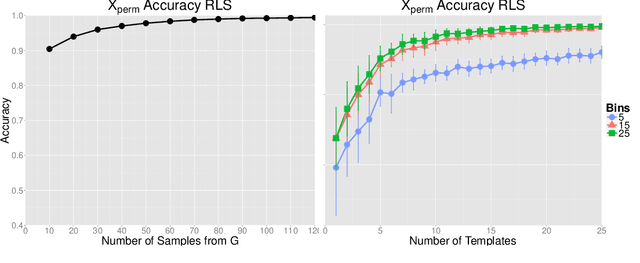
We analyze in this paper a random feature map based on a theory of invariance I-theory introduced recently. More specifically, a group invariant signal signature is obtained through cumulative distributions of group transformed random projections. Our analysis bridges invariant feature learning with kernel methods, as we show that this feature map defines an expected Haar integration kernel that is invariant to the specified group action. We show how this non-linear random feature map approximates this group invariant kernel uniformly on a set of $N$ points. Moreover, we show that it defines a function space that is dense in the equivalent Invariant Reproducing Kernel Hilbert Space. Finally, we quantify error rates of the convergence of the empirical risk minimization, as well as the reduction in the sample complexity of a learning algorithm using such an invariant representation for signal classification, in a classical supervised learning setting.

Random Maxout Features

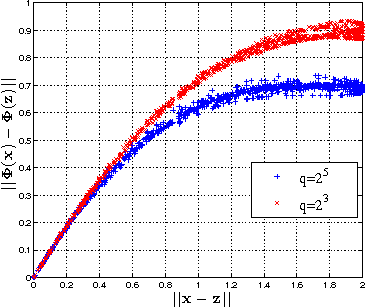
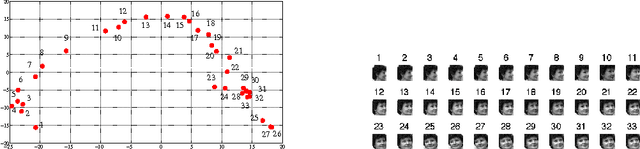
In this paper, we propose and study random maxout features, which are constructed by first projecting the input data onto sets of randomly generated vectors with Gaussian elements, and then outputing the maximum projection value for each set. We show that the resulting random feature map, when used in conjunction with linear models, allows for the locally linear estimation of the function of interest in classification tasks, and for the locally linear embedding of points when used for dimensionality reduction or data visualization. We derive generalization bounds for learning that assess the error in approximating locally linear functions by linear functions in the maxout feature space, and empirically evaluate the efficacy of the approach on the MNIST and TIMIT classification tasks.

Convex Learning of Multiple Tasks and their Structure

Reducing the amount of human supervision is a key problem in machine learning and a natural approach is that of exploiting the relations (structure) among different tasks. This is the idea at the core of multi-task learning. In this context a fundamental question is how to incorporate the tasks structure in the learning problem.We tackle this question by studying a general computational framework that allows to encode a-priori knowledge of the tasks structure in the form of a convex penalty; in this setting a variety of previously proposed methods can be recovered as special cases, including linear and non-linear approaches. Within this framework, we show that tasks and their structure can be efficiently learned considering a convex optimization problem that can be approached by means of block coordinate methods such as alternating minimization and for which we prove convergence to the global minimum.